Методика расчета числа наблюдений, необходимого для получения достоверного результата.
Может случиться так, что при расчете достоверности относительных величин или их разности получаемые выводы будут свидетельствовать об их недостоверности. В этих случаях оперировать такими показателями или делать какие-либо выводы и заключения на их основе невозможно.
Теоретически выход из данного положения имеется: для получения достоверных результатов необходимо увеличить число наблюдений. В этом случае возникают два вопроса: какое число наблюдений будет минимальным для достижения требуемой цели и каким образом можно рассчитать это число.
Рассчитать число наблюдений, необходимое для получения достоверного результата можно исходя из формулы расчета ошибки относительного показателя, предварительно введя в нее критерий достоверности результата:
m =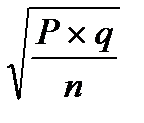 
; умножаем правую и левую t 
m = t 
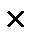
части формулы на t
Для того, чтобы избавиться от квадратного корня, возведем обе части уравнения в квадрат:
( t 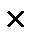m )2 = 
Величина t 
m называется предельной ошибкой показателя, обозначается буквой 
и задается самим исследователем. Отсюда:
n = 
Где t может принимать значения 1, 2, 3 соответственно вероятностям достоверности результатов 0,68; 0,95; 0,997.
Приведем пример такого расчета: из данных научной литературы известно, что удельный вес здоровых детей среди новорожденных составляет 36%. Какое число наблюдений необходимо для того, чтобы подтвердить или опровергнуть этот вывод? Обратимся к формуле для расчета необходимого числа наблюдений:
|
|
|
n =
Примем t = 2, т.к. вероятность достоверности результата 0,95 в данном случае достаточна; Р = 36%, тогда q = 100 - Р = 100 - 36 = 64%. Предельную ошибку примем равной 5%.
n = 
= 369
Следовательно, для подтверждения данного вывода с вероятностью достоверности результата 0,95 необходимо взять для наблюдения 369 новорожденных.
В тех случаях, когда в литературных источниках исходных данных нет и закономерности явления не изучены, а пробное исследование трудноосуществимо, то допускают, что величины Р и q будут одинаковы и Р = q = 50 %, и тогда величина произведения Р 
q будет максимально большой (2500%).
И, наконец, в случае, если величина показателя равна 0% или 100%, число наблюдений для получения достоверного результата может быть определено по формуле:
если m =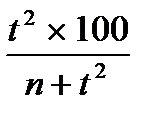 
, тогда n + t 2 = 
; n = 
- t 2
Рассчитаем необходимое число наблюдений для такого случая, вернувшись к примеру 100% эффективности нового лекарственного препарата, где были следующие условия:
число лечившихся больных (n) = 100
показатель эффективности лечения (Р) = 100 %
m = =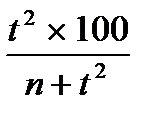 
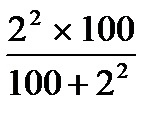= 3,8 %
|
|
|
Для подтверждения этого вывода с высокой степенью достоверности - 0,997 (тогда t = 3) нам необходимо провести проверку эффективности нового лечебного препарата на группе больных численностью:
n = 
- t 2 = 
человек,
а не 100 человек, как это было сделано.
ольше. Важно, что средняя получается для каждого уровня
21.
t-критерий Стьюдента – общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках.
Для сравнения средних величин t-критерий Стьюдента рассчитывается по следующей формуле:
где М1 - средняя арифметическая первой сравниваемой совокупности (группы), М2 - средняя арифметическая второй сравниваемой совокупности (группы), m1 - средняя ошибка первой средней арифметической, m2 - средняя ошибка второй средней арифметической.
Дата добавления: 2019-07-15; просмотров: 167; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!