Расчет достоверности разности двух относительных
Величин.
Для расчета достоверности разности двух относительных показателей используется специальная формула, предложенная английским ученым Стьюдентом:
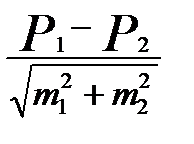= t
где Р1 и Р2 - сравниваемые относительные показатели
m1 и m2 - ошибки сравниваемых показателей
t - критерий достоверности.
Величина критерия всегда получается и оценивается в абсолютных числах и без учета знака, получившегося при расчете величины разности Р1 и Р2.
Оценка результата, полученного при вычислении критерия достоверности, в значительной степени зависит от числа наблюдений (n) в ходе исследования. Для того, чтобы признать разность относительных величин достоверной, необходимо иметь следующие значения критерия:
а) при n > 100 t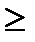 
2,6
б) при 30 < n < 100 t 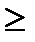3
в) при n < 30 t определяется по специальным таблицам Стьюдента-Фишера.
Таблица значений критерия t (Стьюдента)
| Вероятность ошибки (Р) |
0,05 = 5 % |
0,01 = 1 % |
0,001 = 0,1 % |
| Число степеней свободы (n) | |||
| 1 | 12,70 | 63,66 | 637,59 |
| 2 | 4,30 | 9,92 | 31,60 |
| 3 | 3,18 | 5,84 | 12,94 |
| 4 | 2,78 | 4,60 | 8,61 |
| 5 | 2,57 | 4,03 | 6,86 |
| 6 | 2,42 | 3,71 | 5,96 |
| 7 | 2,36 | 3,50 | 5,31 |
| 8 | 2,31 | 3,36 | 5,04 |
| 9 | 2,26 | 3,25 | 4,78 |
| 10 | 2,23 | 3,17 | 4,59 |
| 11 | 2,20 | 3,17 | 4,44 |
| 12 | 2,18 | 3,06 | 4,32 |
| 13 | 2,16 | 3,01 | 4,22 |
| 14 | 2,14 | 2,98 | 4,14 |
| 15 | 2,13 | 2,95 | 4,07 |
| 16 | 2,12 | 2,92 | 4,02 |
| 17 | 2,11 | 2,90 | 3,96 |
| 18 | 2,10 | 2,88 | 3,92 |
| 19 | 2,09 | 2,86 | 3,88 |
| 20 | 2,09 | 2,84 | 3,85 |
| 21 | 2,08 | 2,83 | 3,82 |
| 22 | 2,07 | 2,82 | 3,79 |
| 23 | 2,07 | 2,81 | 3,77 |
| 24 | 2,06 | 2,80 | 3,75 |
| 25 | 2,06 | 2,79 | 3,73 |
| 26 | 2,06 | 2,78 | 3,71 |
| 27 | 2,05 | 2,77 | 3,69 |
| 28 | 2,05 | 2,76 | 3,67 |
| 29 | 2,04 | 2,76 | 3,66 |
| 30 | 2,04 | 2,75 | 3,64 |
|
|
|
Рассмотрим методику расчета достоверности разности двух относительных величин на следующем примере:
В районе А. с населением 10000 человек показатель заболеваемости гриппом составил 50 ‰ (Р1), в районе В. с таким же населением этот показатель был равен 30 ‰ (Р2). Нам необходимо выяснить, действительно ли заболеваемость гриппом выше в районе А., чем в районе В., или же эта разность несущественна.
Р1 = 50 ‰ ; n1 = 10000 ; m1 =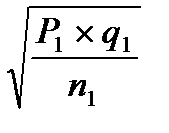 
= 
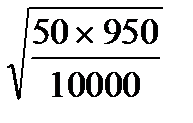= ± 2,2 ‰
Р2 = 30 ‰ ; n2 = 10000 ; m2 =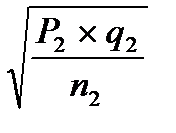 
= 
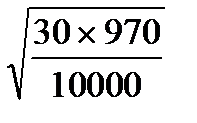= ± 1,7 ‰
t = =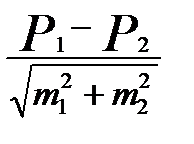 
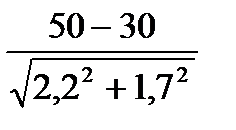= 7,2
Число наблюдений в нашем примере 10000 (больше 100), величина критерия Стьюдента 7,2 (больше 2,6), следовательно, мы с большой достоверностью можем утверждать, что различие сравниваемых показателей существенно, т.е. в районе А. заболеваемость гриппом действительно выше, чем в районе В.
Рассмотрим еще один пример:
При анализе годового отчета главный врач участковой больницы обнаружил, что в 1995 году доля заболевших ангинами составила 2,5% от общего числа заболевших, а в 1996 году доля таких больных была 4,0%.
|
|
|
Достоверно ли увеличение доли заболевших ангиной? Ответ на этот вопрос можно дать, рассчитав достоверность разности этих показателей:
При различных числах наблюдений в сравниваемых группах оценка критерия Стьюдента должна производиться по требованиям для группы с меньшим числом наблюдений. Следовательно, чтобы разность показателей в нашем примере была достоверной, величина критерия t должна быть равна или больше 3, т.к. число наблюдений в опыте (n1 = 95) меньше 100, но больше 30.
Полученный результат значительно меньше требуемой величины критерия t, следовательно, действительного увеличения удельного веса заболевших ангиной не произошло.
Расчет и сопоставление доверительных интервалов сравниваемых относительных показателей.
Мы уже подробно рассмотрели вопрос, почему при характеристике какого-либо явления нельзя ограничиваться только расчетом относительных величин и с какой целью необходимо в ходе анализа рассчитывать их доверительные интервалы. Поэтому, не останавливаясь на методике и смысле этих действий, произведем вычисление доверительных интервалов для двух относительных показателей. Для этого используем пример о заболеваемости гриппом в районе А. и районе В.
|
|
|
Район А.: Р1 = 50 ‰ ; n1 = 1000; m1 = ± 2,2 ‰
Р1 ± 2m1 = 50 ± 2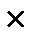 
2,2 = 45,6 - 54,4 ‰
Район В.: Р2 = 30 ‰ ; n2 = 1000; m2 = ± 1,7 ‰
Р2 ± 2m2 = 30 ± 2 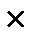1,7 = 26,6 - 33,4 ‰
Теперь, для большей наглядности полученного вывода, представим результаты расчетов доверительных интервалов графически на числовой оси:
Р2 ± 2m2 Р1 ± 2m1
0 10 20 26,6 30 33,4 40 45,6 50 54,4 60
Как видно из графика, на числовой оси между интервалами, занимаемыми обоими показателями, имеется промежуток, у них нет общих друг с другом значений, или, как говорят, не произошло наложение интервалов. В таких случаях делается вывод: разность показателей достоверна, существенна, т.е. действительно заболеваемость населения гриппом в районе А. выше, чем в районе В. Если бы доверительные интервалы этих показателей имели бы общие друг с другом значения, т.е. если бы произошло наложение интервалов, то разность показателей следовало бы признать недостоверной, не существенной.
Описанная методика расчета достоверности разности двух относительных величин достаточно проста и надежна, но для ее использования необходимо помнить, что применяться она может лишь при условии одинаковых или очень близких друг с другом чисел наблюдений - n, на которых были получены исследуемые относительные коэффициенты.
|
|
|
Дата добавления: 2019-07-15; просмотров: 339; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!