ПОКАЗАТЕЛИ ДИНАМИЧЕСКОГО РЯДА. МЕТОДИКА РАСЧЕТА.
Динамический ряд - это ряд статистических величин, показывающих изменение их во времени, расположенных в хронологическом порядке через определенные промежутки времени.
Динамические ряды могут быть моментными, когда величины ряда характеризуют явление на какой-то определенный момент времени (штаты, койки, вновь выявленные больные при медосмотрах и т.д.) и интервальными, когда явление рассматривается за определенный период (число родившихся и умерших за год, число поступивших больных в стационар, число бытовых травм за месяц и др.).
Величины, из которых состоит динамический ряд, называются уровнями ряда. Если динамический ряд состоит из абсолютных чисел, то он называется простым, если из относительных или средних величин - то сложным или производным.
Для характеристики динамического ряда используют 3 основных показателя:
· 18тный прирост (убыль) - разность между последующим и предыдущим уровнем
· темп прироста - процентное отношение абсолютного прироста (убыли) к предыдущему уровню
· темп роста - процентное отношение последующего уровня к предыдущему уровню.
Рассмотрим методику анализа динамического ряда на примере изменения показателя общей смертности в России с 1940 по 1995 годы:
| Годы | Уровень смертности, ‰ | Абсолютный прирост (убыль) | Темп роста, % | Темп прироста, % |
| 1940 1960 1970 1980 1990 1995 | 20,6 7,4 8,7 11,0 11,2 15,0 | - - 13,2 1,3 2,3 0,2 3,8 | - 35,9 117,6 126,4 101,8 133,9 | - - 64,1 17,6 26,4 1,8 33,9 |
Пример расчета:
|
|
|
1) абсолютный прирост (убыль) = последующий уровень - предыдущий уровень
1940-1960 гг. = 7,4 - 20,6 = - 13,2
1970-1960 гг. = 8,7 - 7,4 = 1,3
1980-1970 гг. = 11,0 - 8,7 = 2,3
и т.д.
2) Темп роста = последующий уровень х 100% / предыдущий уровень
1940-1960 гг. = 7,4 х 100 / 20,6 = 35,9%
1970-1960 гг. = 8,7 х 100 / 7,4 = 117,6%
1980-1970 гг. = 11 х 100 / 8,7 = 126,4%
и т.д.
3) Темп прироста = абс. прирост х 100 / предыдущий уровень
1940-1960 гг. = - 13,2 х 100 / 20,6 = - 64,1
1970-1960 гг. = 1,3 х 100 / 7,4 = 17,6
1980-1970 гг. = 2,3 х 100 / 8,7 = 26,4
и т.д.
Многочисленные наблюдения за длительный промежуток времени не всегда позволяют выявить определенную тенденцию в динамике. Такую возможность дает применение методов выравнивания динамических рядов. К ним относятся:
1. Приведение рядов к одному основанию путем вычисления показателей наглядности. Динамика в этом случае выразится наиболее ярко.
2. Укрупнение интервалов, которое заключается в суммировании данных за ряд периодов. В результате получаются итоги за более продолжительные отрезки времени и тем самым сглаживаются случайные колебания и более четко определяется характер динамики.
3. Сглаживание путем групповой и скользящей средней. Периоды времени укрупняются и для них вычисляется средняя величина, характеризующая укрупненный период. Этим достигается большая ясность изменений во времени.
|
|
|
Интересен метод скользящей средней, который часто применяется для характеристики сезонных колебаний. Для этого каждый уровень ряда заменяется средней из данного уровня и соседних с ним. Обычно суммируются последовательно три члена ряда, но можно брать и б1. Вычисление ошибки относительной величины.
Ошибка относительной величины обозначается знаком ( m ) и рассчитывается по следующей формуле:
m =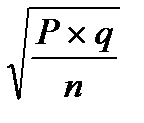 
где Р - относительная величина,
q - альтернатива (величина, противоположная по значению Р)
q = 1 - Р Если показатель выражен в процентах,
то q = 100 - Р, если в промилле - то q = 1000 - Р и т.д.
n - число наблюдений.
Данная формула используется для определения ошибки относительного показателя при числе наблюдений n>30 (большая выборка). Если же мы имеем дело с малой выборкой (n<30), ошибка относительного показателя должна рассчитываться следующим образом:
m =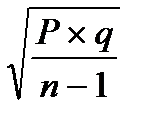 
Произведем расчет ошибки для какого-либо относительного показателя:
В районе А. с населением 10000 жителей зарегистрировано 500 случаев заболевания гриппом. Интенсивный показатель заболеваемости населения гриппом будет равен:
|
|
|
500 х 1000
Р = -------------------- = 50 ‰
10000
(50 случаев заболевания на каждую 1000 населения), следовательно, q = 1000 - 50 = 950
Ошибка этого показателя равна: m = 
= 
= ± 2,2 ‰
Ошибка относительного показателя всегда имеет знак ( ± ) и наименование, соответственно тому показателю, для которого она рассчитывается.
Существует следующее правило: ошибка показателя должна быть в три раза меньше величины самого показателя. Т.е., например, если мы имеем относительный показатель, равный 2,0%, а его ошибка равна ± 0,8%, то такому показателю нельзя доверять, т.к. 0,8 х 3 = 2,4 и 2,0 < 2,4. В нашем примере ошибка в 3 раза меньше полученного показателя, следовательно, ему можно доверять.
Достоверность относительного показателя с помощью ошибки определяется путем расчета доверительного интервала по следующей формуле:
P = Pв ± t 
m
где:
t - доверительный коэффициент, который может принимать значения 1, 2, 3.
Pв - показатель выборочной совокупности.
Если доверительный коэффициент равен 1, т.е. интервал P = Pв ± m, то вероятность того, что при повторных исследованиях показатель не выйдет за пределы данного интервала составляет 0,68 (68%).
|
|
|
Если доверительный коэффициент равен 2, т.е. интервал P = Pв ± 2m, то вероятность того, что при повторных исследованиях показатель не выйдет за пределы данного интервала составляет 0,95 (95%).
Если доверительный коэффициент равен 3, т.е. интервал P = Pв ± 3m, то вероятность того, что при повторных исследованиях показатель не выйдет за пределы данного интервала составляет 0,997 (99,7%).
Какие из этих интервалов можно назвать доверительными?
Из теории вероятностей известно, что вероятность, которой можно доверять, или доверительная вероятность, равная 0,95, считается достаточной для суждения о достоверности полученных результатов опыта. Вероятность, равная 0,997 считается еще более надежным критерием достоверности.
Следовательно, интервалы колеблемости показателя P = Pв ± 2m и P = Pв ± 3m являются доверительными интервалами показателя.
Произведем расчеты интервалов колеблемости показателя в нашем примере: Р = 50 ‰, m = ± 2,2 ‰
P ± m = 50 ± 2,2 = 47,8 - 52,2
P ± 2m = 50 ± 2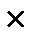 
2,2 = 45,6 - 54,4
P ± 3m = 50 ± 3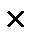 
2,2 = 43,4 - 56,6
Таким образом, мы можем утверждать, что показатель заболеваемости населения гриппом в районе А. фактически может приобретать любые значения в интервале 45,6 - 54,4 ‰ с достоверностью 0,95, и в интервале 43,4 - 56,6 ‰ с достоверностью 0,997. То есть, если при повторных изучениях заболеваемости населения гриппом мы будем получать значения, входящие в эти интервалы, все они будут достоверными.
Таким образом, при анализе любого статистического материала, рассчитав какой-либо относительный показатель, нельзя сразу делать заключение о величине исследуемого явления. Необходимо, рассчитав ошибку этого показателя, обязательно рассчитать один из доверительных интервалов (как минимум P ± 2m) и только тогда делать заключение о величине исследуемого явления.
Так, в нашем примере мы не можем утверждать, что показатель заболеваемости населения гриппом в районе А. составил 50 ‰, мы должны сделать заключение, что он с вероятностью 0,95 колеблется в пределах от 45,6 ‰ до 54,4 ‰ и любое значение этого же показателя в этом интервале, полученное при повторных исследованиях, будет достоверно.
Особый интерес представляет методика расчета ошибки относительного показателя при его значениях, равных 0% и 100%. Действительно, при расчете ошибки показателя по уже представленной форме получаем:
а) Р = 0% ; n = 125 ; m = = 
= 0
б) Р = 100% ; n = 125 ; m = = 
В таких случаях можно сделать ошибочный вывод о том, что у относительной величины нет ошибки, т.е. она абсолютно достоверна. Однако это противоречит закону больших чисел, поскольку эти результаты могут быть получены и на малом числе наблюдений и даже на единичных наблюдениях, следовательно, они обязательно должны отклоняться от математически достоверных величин, т.е. иметь ошибку.
Для таких случаев предложена другая методика расчета ошибки относительной величины:
m = 
где t - доверительный коэффициент
n - число наблюдений.
Приведем пример расчета ошибки относительного показателя, имеющего величину 100%.
В терапевтическом отделении для лечения 100 больных применили новое лекарственное средство, оказавшееся эффективным во всех случаях, т.е. в 100%. Возникает вопрос: действительно ли эффективен этот препарат во всех случаях?
Для того, чтобы ответить на этот вопрос, необходимо рассчитать ошибку полученного показателя:
Р = 100 % ; n = 100
m = ; при t = 2 получим m =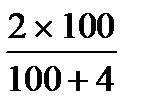 
= 3,8 %
Это означает, что при дальнейшем увеличении числа наблюдений в 95% случаев (т.к. t = 2) препарат будет неэффективен у 3,8% лечившихся больных.
При применении данной формулы ошибка не имеет знака (±), т.к. отклонение показателя может быть только в одну сторону - при 0% в большую, при 100% в меньшую. Кроме того, при определении доверительного интервала нет необходимости удваивать или утраивать ошибку, т.к. введя в формулу величину t мы сразу задаем необходимую его точность.
Дата добавления: 2019-07-15; просмотров: 142; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!