Координация деятельности подразделений и специалистов ЛПУ по реализации целевых программ в части укрепления здоровья и профилактики заболеваний.

⇐ ПредыдущаяСтр 6 из 53Следующая ⇒

Профилактическая программа (либо профилактический фрагмент общей программы)- систематизированное изложение основных целей, задач, направлений деятельности по профилактике заболеваемости, сохранению и укреплению здоровья. Профилактические программы (либо профилактические фрагменты общей программы) включают в себя обоснование и перечень мероприятий по реализации поставленных задач, сроки и условия реализации, исполнителей, ресурсную потребность, ожидаемый результат, а также системы управления, контроля и оценки эффективности.

Мониторинг здоровья и профилактической деятельности.

В структуру отделения профилактики предлагается включить кабинет мониторинга здоровья и профилактической деятельности. Мониторинг – это целенаправленная деятельность, включающая перманентное наблюдение, анализ, оценку и прогноз состояния объекта (процесса, явления, системы) или, иначе – аналитическая система слежения.

Мониторинг здоровья предполагает наблюдение и анализ состояния здоровья прикрепленного населения и его отдельных целевых групп по информации, предоставляемой отделом статистики (заболеваемость по обращаемости, в том числе по отдельным классам и группам заболеваний, полу, возрасту и т.д., заболеваемость по результатам профосмотров, выход на инвалидность, смертность и др.).

Мониторинг профилактической деятельности подразделений отделения профилактики и ЛПУ включает в себя аналитическое слежение за объемами, качеством и эффективностью оказания профилактических и оздоровительных медицинских услуг как в структуре отделения профилактики, так и вцелом в ЛПУ, гигиенического образования и воспитания населения.

9.Социологические исследования в области профилактической деятельности. При решении конкретных проблем укрепления здоровья и профилактики заболеваний, формирования ЗОЖ все большее значение приобретает изучение процессов, происходящих в этом направлении в обществе, что может быть достигнуто при проведении несложных социологических исследований. Планирование и проведение эффективных профилактических вмешательств предполагает изучение степени готовности отдельных групп населения и индивидуумов к обучению и восприятию гигиенических знаний и навыков ведения ЗОЖ.

Социологическое исследование в системе здравоохранения – способ получения знаний о процессах, происходящих в обществе, связанных с отношением к собственному и общественному здоровью, использованию профилактических, оздоровительных, лечебных и реабилитационных вмешательств, оценкой их доступности, эффективности и качества, основанный на получении информации и выявлении закономерностей на основе теорий, методов и процедур, принятых в социологии

13. Теория вероятности и закон больших чисел как теоретическая основа выборочного метода. Требования к выборочному методу. Методы формирования выборочной совокупности.

Разработал П. Лапласна основе закона больших чисел.

Теория вероятностей – математическая наука, изучающая закономерности случайных явлений: «вероятность какого-либо события равна отношению числа наступивших событий к числу всех возможных событий, а вероятность отсутствия какого-либо события равна отношению числа не наступивших событий к числу всех возможных событий».

Чем ближе вероятность наступления события к нулю, тем оно менее вероятно.

Виды событий:

§ Если при каждом осуществлении комплекта условий S обязательно происходит событие A, то оно называется достоверным.

§ Если при осуществлении комплекса условий S событие A заведомо не может произойти, то оно называется невозможным.

§ Случайным называется такое событие A, которое при каждом осуществлении комплекса условий может произойти, но может и не произойти.

Выборочное наблюдение — это вид несплошного наблюдения, основанный на принципе случайного отбора тех единиц исследуемой совокупности, которые должны быть подвергнуты статистическому наблюдению. В структуре выборочной совокупности должны быть представлены все характерные типы единиц, составляющих исследуемую совокупность

Выборочный метод позволяет получить важнейшие социально-гигиенические характеристики: изучается заболеваемость различных социальных групп населения по полу, возрасту, в зависимости от различных факторов, условий и образа жизни. Выделяются группы, включающие детей, подростков, студентов, школьников, рабочих, а также больных с определенными нозологическими формами (сердечно-сосудистые, травмы и др.).

Наиболее распространенным методом оценки достоверности разности между сравниваемыми выборочными результатами является критерий Стьюдента, предложенный В. Госсетом. Критерий t позволяет производить сравнение только между двумя выборочными величинами. Если необходимо сравнить между собой несколько однородных выборочных величин, то они сравниваются поочередно. Критерий достоверности (Стьюдента) определяется как величина разности средних величин или относительных показателей, деленная на извлеченную из квадратного корня сумму квадратов ошибок средних арифметических или относительных показателей. t =

t =

Разница между сравниваемыми выборочными величинами существенна и статистически достоверна при вероятности безошибочного прогноза 95%, т.е. величина критерия Стьюдента должна быть равна или больше 2 (при n >30). Только при этих условиях прогноз считается безошибочным, свидетельствующим о надежности используемого нового метода (лекарственного препарата, гигиенических характеристик).

Мерой достоверности показателя является его ошибка - ошибка представительности (репрезентативности). Ошибка показывает насколько результат, полученный при выборочном исследовании, отличается от результата, который мог бы быть получен при сплошном исследовании всей генеральной совокупности. Средняя ошибка средней арифметической (m) равняется отношению среднеквадратического отклонения к квадратному корню из числа наблюдений. Средняя ошибка относительных показателей рассчитывается по формуле: m =

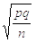
, где р – соответствует величине относительного показателя, q =100 – p, если относительный показатель выражен в процентах, 1000 – р, если показатель вычислен в промилле и т.д. С увеличением числа наблюдений достоверность выборочного результата увеличивается, но это не значит, что следует стремиться бесконечно увеличивать число наблюдений. Это не нужно, а иногда и практически неосуществимо. Относительно небольшой, но качественно однородный статистический материал дает достаточно надежные выводы.

В тех случаях, когда уровень относительного показателя превышает величину основания (общий уровень заболеваемости составил 1300 случаев на 1000 человек), определение ошибки представительности по указанной выше формуле становится невозможным и если показатель находится в пределах от 1,0 до 1,5 в среднем на одного человека, то ошибку представительности следует определять по формуле: m =

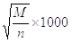
, где М – среднее число заболеваний на одного человека (при заболеваемости 1300‰ – М = 1,3), n –общее число наблюдений

Закон больших чисел.

Математическая статистика изучает статистические закономерности, т.е. такие закономерности, которые проявляют себя лишь при исследовании массы однородных явлений.

В настоящее время существуют точные математические формулировки закона больших чисел. Однако мы воспользуемся более простой формулой этого закона, которая предложена Р.Мизесом.

Закон больших чисел в этом виде может, быть представлен следующей формулой:

lim (X_n - P_n) / n- ¥	→	0

т.е. в пределе при числе наблюдений (n), стремящемся к бесконечности, разность между наблюдаемой частотой какого-либо явления и его математической вероятностью стремится к нулю.

Иначе говоря, фактическая частота наблюдаемого случайного явления совпадает с вычисленной вероятностью его (их разность только при этом условии может быть равна нулю) лишь при достаточно большом числе наблюдений.

Закон больших чисел имеет два важнейших положения для выборочного исследования: 1. по мере увеличения числа наблюдений результаты исследования, полученные на выборочной совокупности, стремятся воспроизвести данные генеральной совокупности;

2. при достижении определенного числа наблюдений в выборочной совокупности результаты исследования будут максимально приближаться к данным генеральной совокупности. Иными словами, при достаточно большом числе наблюдений выявляются закономерности, которые не удается обнаружить при малом числе наблюдений.

Выборка может быть:

собственно-случайная - состоит в том, что выборочная совокупность образуется в результате случайного (непреднамеренного) отбора отдельных единиц из генеральной совокупности.
механическая - состоит в том, что отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы).
типическая – при которойгенеральная совокупность вначале расчленяется на однородные типические группы. Затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность.
серийная - при которой генеральную совокупность делят на одинаковые по объему группы - серии.
комбинированная - выборка может быть двухступенчатой. При этом генеральная совокупность сначала разбивается на группы. Затем производят отбор групп, а внутри последних осуществляется отбор отдельных единиц.

14. Требования к выборочному методу. Методы формирования выборочной совокупности.

Теоретические основы медико-биологической статистики. Генеральная и выборочная совокупность. Методы формирования выборочной совокупности.

Медицинская (или санитарная) статистика представляет собою одну из ветвей статистической науки и изучает явления общественной жизни, связанные с медициной, гигиеной, санитарией и здравоохранением. Медицинская статистика делится обычно на два основных раздела:

1. Статистика здоровья населения, к задачам которой относится:

а) изучение состояния здоровья населения (воспроизводство населения, продолжительность жизни, заболеваемость, физическое развитие и др.);

б) выявление и установление связей между уровнем заболеваемости и смертности населения с различными факторами окружающей среды.

2. Статистика здравоохранения, задачами которой являются:

а) определение показателей, характеризующих качество работы лечебно-профилактических учреждений и отдельных врачей и позволяющих объективно оценивать их деятельность;

б) сбор и изучение данных о сети, кадрах и деятельности медицинских учреждений, необходимых для планирования здравоохранения и контроля за выполнением планов;

в) статистическое исследование мероприятий по предупреждению и лечению заболеваний.

Кроме того, особое место в медицинской статистике занимают методы, применяемые, для оценки достоверности результатов экспериментов, проводимых в лабораториях или клиниках.

Медицинская статистика, как и статистическая наука вообще, при оценке количественных отношений руководствуется понятиями и положениями математических наук - теории вероятностей и математической статистики. Некоторые основные понятия необходимо разобрать подробнее.

Генеральная совокупность — вся изучаемая выборочным методом статистическая совокупность объектов и/или явлений общественной жизни (единиц отбора), имеющих общие качественные признаки или количественные переменные.

Выборочная совокупность (выборка) — представительная часть генеральной совокупности. Процесс выборки основан на правомерности выводов о целом на основании изучения его части при условии, что по своей структуре эта часть является микромоделью целого.

Выборочная совокупность – уменьшенная модель генеральной совокупности; те, кому социолог раздает анкеты, кто называется респондентами, кто, наконец, представляет собой объект социологического исследования. Иначе говоря, это множество людей, которых социолог опрашивает.

Полный и точный перечень единиц выборочной совокупности образует основу выборки. Элементы, предназначенные для отбора, называются единицами отбора.

Если основа выборки включает список единиц отбора, то структура выборки подразумевает их группировки по каким-то важным признакам, например, распределение индивидов по профессии, квалификации, полу и возрасту. Таким образом, структура выборки – это процентные пропорции признаков объекта, на основании которых составляется выборочная совокупность.

Если тип выборки говорит о том, как попадают люди в выборочную совокупность, то объем выборки сообщает о том, какое количество попало в нее. Объем выборки – количество единиц выборочной совокупности. Поскольку выборочная совокупность (или выборка, что одно и то же) – это часть генеральной совокупности, отобранной с помощью специальных методов, - поскольку ее объем всегда меньше объема генеральной.

Расхождение между генеральной и выборочной совокупностью называется ошибкой репрезентативности, допустимое склонение – 5%.

Способы формирования выборочной совокупности.

Существует несколько классификаций:

I. По методу отбора:

1) повторный отбор, т.е. единицу, попавшую в выборку после регистрации, снова возвращают в генеральную совокупность, и она сохраняет равную возможность со всеми прочими единицами вновь попасть в выборку;

2) бесповторный отбор, т.е. единица, попавшая в выборку, не возвращается в генеральную совокупность.

II. По способу отбора:

1) собственно случайная выборка, т.е. отбор единиц из генеральной совокупности осуществляется наугад (используется метод жеребьёвки или таблица случайных чисел);

2) механическая выборка, которая применяется, когда генеральная совокупность упорядочена. При этом заданное число единиц отбирают механически через определённые интервалы (например, если надо отобрать 10%, то отбирается каждая 10-я единица);

3) типическая выборка, которая используется, когда все единицы генеральной совокупности разбиты на типические группы. При этом из каждой типической группы собственно случайной или механической выборкой производится отбор единиц в выборочную совокупность;

4) серийная выборка, которая используется, когда единицы генеральной совокупности объединены в небольшие группы или серии (например, студенческие группы, упаковка продукции и т.д.). При данном отборе отбираются случайно или механически отдельные серии, которые изучаются полностью.

15. Статистическая совокупность и ее структура. Сплошное и выборочное статистическое наблюдение. Понятие о репрезентативности. Систематические и случайные ошибки статистического анализа.

Статистическая совокупность — группа, состоящая из множества относительно однородных элементов, взятых вместе в известных границах пространства и времени и обладающих признаками сходства и различия.

Свойства статистической совокупности:

1) однородность единиц наблюдения

2) определенные границы пространства и времени изучаемого явления.

Статистическая совокупность состоит из отдельных, единичных наблюдений.

Единица наблюдения — каждый первичный элемент, составляющий статистическую совокупность и являющийся носителем признаков, подлежащих учету.

Различают два вида статистической совокупности :

А) генеральная совокупность — совокупность, состоящая из всех единиц наблюдения, которые могут быть к ней отнесены в соответствии с целью исследования.

Б) выборочная совокупность — часть генеральной, отобранная специальным (выборочным) методом и предназначенная для характеристики генеральной совокупности.

Сплошное наблюдение — это такой вид статистического наблюдения, при котором обследованию подвергаются все единицы изучаемой совокупности. Основной предпосылкой подобного наблюдения является определение подлежащих регистрации признаков.

Выборочное наблюдение — это вид несплошного наблюдения, основанный на принципе случайного отбора тех единиц исследуемой совокупности, которые должны быть подвергнуты статистическому наблюдению. В структуре выборочной совокупности должны быть представлены все характерные типы единиц, составляющих исследуемую совокупность.

Репрезентати́вность — соответствие характеристик выборки характеристикам популяции или генеральной совокупности в целом. Репрезентативность определяет, насколько возможно обобщать результаты исследования с привлечением определённой выборки на всю генеральную совокупность, из которой она была собрана.

Ошибки регистрации — представляют собой отклонения между значением показателя, полученного в ходе статистического наблюдения, и его фактическим значением.

Ошибки репрезентативности — возникают, когда отобранная совокупность недостаточно точно воспроизводит исходную совокупность. Характерны для несплошного наблюдения и заключаются в отклонении величины показателя исследуемой части совокупности от его величины в генеральной совокупности.

Случайные ошибки — являются результатом действия случайных факторов.

Систематические ошибки — всегда имеют одинаковую направленность к увеличению или уменьшению показателя по каждой единице наблюдения, вследствие чего значение показателя по совокупности в целом будет включать накопленную ошибку.

16. Статистическое исследование в медицине и биологии. Доверительные интервалы, доверительная вероятность и уровень статистической значимости. Репрезентативность.

1. Статистика здоровья населения, к задачам которой относится:

2. Статистика здравоохранения, задачами которой являются:

в) статистическое исследование мероприятий по предупреждению и лечению заболеваний.

Доверительная вероятность.

Оперируя понятием вероятность, всегда следует помнить о том, что как бы ни мала была вероятность какого-либо события, до тех пор пока она не равна нулю (т.е. пока это событие не является невозможным), оно все же может произойти и, наоборот, как бы ни велика была вероятность события, но пока она не равняется единице (т.е. пока событие не является достоверным) оно может и не произойти.

В популярном в свое время кинофильме «Два бойца», вышедшем на экраны в годы Отечественной войны, имеется образ профессора-математика, который в начале войны в момент объявления воздушной тревоги не ходил в бомбоубежище, так как определил, то площадь его квартиры по отношению к площади всего Ленинграда настолько мала, что вероятность того, что одна из брошенных фашистами бомб попадет именно в его квартиру, имеет ничтожное значение.

Однако после того как в Ленинградском зоопарке, во время одной из бомбежек был убит единственный в городе слон (как ни мала была вероятность этого события, оно все же случилось), профессор пересмотрел свою точку зрения и стал спускаться в убежище.

Вот почему, оперируя показателями вероятности, теория вероятностей всегда имеет в виду не столько результат единичного испытания, сколько проявление этой закономерности в массе однородных явлений, о чем уже говорилось в самом начале настоящего пособия.

Однако, в целях практического применения теории вероятностей в области математической статистики, вводится понятие доверительной вероятности, т.е. такойвеличины вероятности, которая достаточна для того, чтобы полученные результаты опытов считать достоверными.

Вполне понятно, что величина доверительной вероятности весьма относительна и зависит от характера явления, для которого определяется.

Например, если мы знаем, что вероятность выпуска заводом брака артиллерийских снарядов равна 0,01, то ее можно считать малой и пренебречь, так как на фронте стреляют обычно большими сериями снарядов и, если имеется вероятность, что только один из каждой сотни выпущенных снарядов может не разорваться, то это существенного значения не имеет.

Представьте теперь, что такова же вероятность брака на фабрике, выпускающей парашюты. Можно ли в этом случае считать вероятность малой и пренебречь ею? Конечно нет, ведь один из каждых ста парашютистов, воспользовавшихся парашютами этой фабрики, может разбиться. Очевидно, что в этом случае вероятность брака даже равная 0,001 будет велика и недопустима.

Несмотря на относительный характер величины доверительной вероятности в математической статистике для обычных исследований в области биологии и медицины условно приняты два ее значения:

а) Вероятность равная 0,95 — считается достаточной для суждения о достоверности полученных результатов опыта.

б) Вероятность равная 0,997 — считается еще более надежнымкритерием достоверности.

И, наоборот, если полученные результаты имеют вероятность соответственно менее 0,05 или 0,003, то они считаются настолько недостоверными, что ими можно пренебречь

17. Методика статистического исследования, основные этапы, сводка и обработка материалов исследования, основные методы построения статистических таблиц, графическое отображение статистических данных.

2тема. Листочки

18. Содержание плана и программы статистического исследования. Виды статистических таблиц и правила их построения.

19. Медицина, основанная на доказательствах. Основные методы оценки достоверности результатов статистического исследования.

Доказательная медицина – это использование результатов лучших клинических исследований для выбора лечения конкретного пациента, это интеграция лучших научных доказательств с клиническим опытом и ожиданиями пациентов. Принципы доказательной медицины используются, прежде всего, в клинической практике, однако они применимы к любой области медицинской науки, включая профилактическую медицину, общественное здоровье, организацию здравоохранения. Однако при этом следует учитывать, что не все принципы доказательной медицины могут быть применимы в областях, не связанных с клинической практикой.

20. Относительные величины в статистике, их значение и применение. Основные ошибки применения относительных величин.

21.Критерий Стьюдента. Понятие репрезентативности исследования в медицине. Определение достоверности различия двух показателей (2 способа).

22.Динамические ряды. Основные показатели, характеризующие динамический ряд.

Одной из разновидностей производных величин являются относительные величины, в практике часто называемые коэффициентами или относительными показателями (Р).

Относительная величина получается в результате деления одной абсолютной величины (а) на другую (в):

а Р = ------------ х 100 (1000; 10 000 и т.д.) в

Так как в результате деления одного целого числа на другое как правило получается дробное число, то его принято умножать на 100, 1000, 10000 , соответственно полученный результат будет измеряться в процентах ( % ), промилле ( ‰ ), продецимилле ( ‰ ).

Вернемся к нашему примеру. Зная численность населения каждого из районов, мы можем рассчитать относительные показатели - показатели рождаемости в районе А. и районе Б. Среднегодовая численность населения района А. составила 250000 человек, а района Б. - 130000 человек. Следовательно, показатель рождаемости (число родившихся живыми за год на 1000 населения) в районе А. составит:

3800 х 1000

Р _А= ---------------------- = 15,2 ‰

250000

в районе Б:

2500 х 1000

Р _Б = ---------------------- = 19,2 ‰

130000

Если бы мы для оценки рождаемости сопоставляли между собой абсолютные величины, то сделали бы ошибочный вывод, так как абсолютное число рождений в районе А. выше. В действительности же, проведя расчет рождений на каждую тысячу населения получаем обратный вывод: рождаемость выше в районе Б.

Дата добавления: 2019-07-15; просмотров: 186; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!