Данная задача проста и наглядна в своей постановке для учащихся.

Представим себе сосуд, из которого вытекает вода. В момент времени t поток воды вычисляется по формуле q= q( t). Найдем объем воды, вытекающей из сосуда за промежуток времени [t₁; t₂]. Объем воды, находящейся в сосуде, обозначим через V. Этот объем со временем меняется, т. е. V есть функция времени t.

Рассмотрим промежуток времени [t₁; t₂]. Очевидно, что за это время из сосуда вытечет V( t₂)- V( t₁) воды. С другой стороны, поток воды – это величина, характеризующая скорость изменения количества воды в сосуде, т.е. dV= q( t) dt. Следовательно, вычисление объема воды, вытекающей из сосуда за промежуток времени [t₁; t₂], сводится к отысканию первообразной функции q( t).

  Разность V( t₂)- V( t₁) называют интегралом от функции q ( t ) на отрезке [t ₁ ; t ₂] и обозначают так:

.

Все вышерассмотренные модели – это наиболее часто встречающиеся в школьном курсе физики законы и формулы, поэтому они не требуют от учащихся дополнительных знаний по физике, а, следовательно, удовлетворяют как принципу научности, так и принципу доступности материала.

Изучение свойств определенного интеграла с помощью физических моделей

 

При изучении интеграла существенным является отбор свойств, которые необходимо знать ученикам. Их должно быть достаточно для рассмотрения приложений интеграла и в то же время не должны вводиться свойства, без которых можно обойтись в дальнейшем. Доказательство свойств при разных подходах к введению понятия интеграла может быть разным.

Ниже приведенные свойства интеграла рассматриваются на различных физических моделях.

1⁰. .

Рассмотрим доказательство данного свойства на задаче о перемещении точки.

При введении интеграла рассматривается случай, когда нижний предел интегрирования меньше верхнего. Но определенный интеграл можно обобщить и на случай, когда верхний предел меньше нижнего. В этом случае обратимся к определению интеграла как суммы. Разбивая отрезок от [a ; b] промежуточными значениями t ₁ , t ₂ , …, t_{n -1}, убедимся, что все Δt теперь отрицательны. Легко убедиться, что

,     (1)

так как при любом разбиении отрезка [a ; b] соответствующие суммы будут отличаться знаками всех Δt во всех слагаемых. [7]

2⁰. .

Докажем свойство на примере задачи о перемещении точки.

Существенное свойство интеграла состоит в том, что область интегрирования можно разбить на части: путь, пройденный за время от а (начала) до b (конца), можно представить

 

как сумму пути, пройденного за время от a до c (промежуточного момента) и от c до b

.      (2)

При помощи соотношения (1) можно распространить формулу (2) и на случай, когда с не лежит внутри промежутка [a ; b].

Пусть c > b > a. Тогда очевидно

.

Перенесем последнее слагаемое в левую часть и воспользуемся (1)

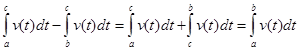.   (3)

Таким образом, получили равенство (3), в точности совпадающее с (2).

Аналогично можно рассмотреть случаи другого расположения чисел a , c , b (их всего шесть вариантов). Учащиеся легко могут самостоятельно убедиться, что формула (2) оказывается верной во всех этих случаях, т. е. независимо от взаимного расположения чисел a , c , b.[7]

Выведенное свойство называется свойством аддитивности интеграла.

3⁰. , .

Рассмотрим доказательство этих свойств на примерах задачи о работе переменной силы и задачи о давлении жидкости на стенку.

3.1. Пусть к материальной точке, движущейся по оси х, приложены две силы F ₁ ( x ) и F ₂ ( x ), направленные по одной прямой в одну сторону. Под действием этих сил материальная точка переместилась из точки а в точку b, при этом работа каждой силы на этом отрезке вычисляется по формулам: 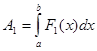 и . Тогда общая работа, совершенная обеими силами равна

.              (4)

С другой стороны, если к телу приложены две силы F ₁ ( x ) и F ₂ ( x ), направленные по одной прямой в одну сторону, то их равнодействующая F ( x ) находится по формуле F ( x )= F ₁ ( x )+ F ₂ ( x ). Работа этой силы равна

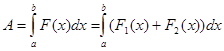.        (5)

В силу равенства левых частей в формулах (4) и (5), получаем равенство правых, т. е.

.

Нетрудно показать, что данное свойство выполняется для любого конечного числа сил, действующих на точку и направленных по одной прямой в одну сторону. Это свойство показывает, что интеграл суммы нескольких слагаемых разбивается на сумму интегралов отдельных слагаемых.

Если же к материальной точке, движущейся по оси х, приложены две силы F₁( x) и F₂( x), направленные по одной прямой, но в противоположную сторону, то их равнодействующая F( x) при F₁( x)> F₂( x) находится по формуле F( x)= F₁( x)- F₂( x). Тогда верно следующее равенство

.

3.2. Ранее был приведен метод введения интеграла, основанный на рассмотрении задачи о давлении жидкости на прямоугольную стенку бассейна с основанием а, в результате решения которой получена формула

,           (6)

где а – величина постоянная, равная ширине стенки бассейна.

Разделим прямоугольную стенку бассейна на а прямоугольников с основанием, равным единице. Тогда весь бассейн также разделится на а равных частей, при чем давление на прямоугольную стенку с основанием, равным единице в каждой части будет вычисляться по формуле . Учитывая, что во всех частях давление одно и то же и всего частей а, то общее давление равно

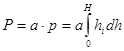.                 (7)

В силу равенства левых частей в формулах (6) и (7), получаем равенство правых, т. е.

.

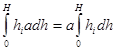Данное равенство можно обобщить на произвольную непрерывную функцию F( x) и произвольный отрезок [a; b], т. е.

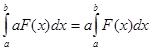
Выведенные формулы в пунктах 3.1 и 3.2 называются свойствами линейности интеграла.

4⁰. Если  на отрезке [a ; b], то .

Докажем данное свойство с помощью задачи о массе стержня.

При введении понятия интеграла с помощью задачи о вычислении массы неоднородного стержня была получена формула

.

Как известно, плотность вещества – это физическая величина, показывающая, чему равна масса вещества в единице объема, следовательно, это величина неотрицательная. С другой стороны масса вещества есть также величина неотрицательная. Таким образом, получаем: если подынтегральная функция неотрицательна на рассматриваемом отрезке, то

.

Используемые в доказательствах свойств физические модели, во-первых, наглядны, во-вторых, при соответствующей методике введения понятия интеграла, данная методика введения свойств заставляет постоянно повторять пройденное, вспоминать выведенные при введении формулы. Все это удовлетворяет принципу прочности знаний и наглядности в обучении (приложение).

 

2.3. Физические модели при отработке техники интегрирования.

 

---

Дата добавления: 2019-07-15; просмотров: 203; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!