Физические модели при изучении темы «Интеграл»
Введение понятия интеграла с помощью физических моделей
После анализа достоинств и недостатков школьных учебников математики относительно темы «Интеграл», после ознакомления с некоторыми учебниками физики и, учитывая психолого-педагогические и методические основы изучения интеграла, мною была разработана методика изучения понятия интеграла с использованием физических моделей в школьном курсе математики, представленная в данной главе.
Нижеследующая методика введения понятия интеграла с помощью задач физики разрабатывалась мной на основе следующего факта.
Физические величины, вычисляемые с помощью интеграла, можно разделить на два типа, в зависимости от того, как они естественно определяются. К первому типу относятся «первичные» величины (длина пути, масса, количество электричества, количество теплоты и т. п.), т. е. такие величины, для которых другие, связанные с ними («вторичные») величины (соответственно скорость, линейная плотность, величина тока, удельная теплоемкость и т. п.) определяются как производные этих величин. Ко второму типу относятся такие, которые определяются естественным образом как интегралы от «первичных» по отношению к ним величин (например, площадь, работа). Для первого типа величин интегральная формула для их вычисления может и должна быть доказана, опираясь на известное из предыдущего материала определение «вторичной» величины как производной от данной «первичной». Для второго типа интегральная формула появляется по определению.[5]
|
|
|
В соответствии с этим рассмотрим описанные в первой главе подходы на конкретных физических моделях из разных разделов физики (механика, электродинамика, кинематика и др.), уделив особое внимание второму подходу, поскольку в школьных учебниках он практически не используется.
При введении понятия интеграла как предела интегральных сумм довольно наглядным и понятным для учащихся является пример задачи о давлении жидкости на стенку.
Задача. Бассейн высоты H наполнен водой. Вычислить давление воды на прямоугольную стенку бассейна с основанием прямоугольника, равным а.
Разделим высоту Н на n равных частей (Δh). Стенка разделится на «элементы». Так как кубометр воды весит тонну, то давление столба жидкости высоты hi м, имеющего сечение 1 м2, равно hi тоннам.
Давление же воды на элемент, находящийся на глубине hi, равно произведению hi на площадь элемента: hia Δh. Обозначим произведение hia через F ( hi ). Тогда величина давления на всю стенку приближенно равна
Pn ≈ F 1 ( h 1 )Δh 1 +…+ Fn ( hn ) Δhn .
Данную сумму называют интегральной суммой функции F( h) на отрезке [0; H]. При этом предполагается, что функция F( h) непрерывна на отрезке [0; H] и может принимать любые значения. Если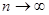 
и высоты «элементов» стремятся к нулю, то точное выражение суммы равно 
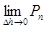. Его называют определенным интегралом от функции F( h) на отрезке [0; H] и обозначают 
.
|
|
|
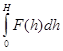Далее понятие определенного интеграла обобщается на произвольную непрерывную функцию F ( x ) и произвольный отрезок [a ; b].
Рассмотрим несколько задач с физическими моделями, где интеграл определяется как приращение первообразной.
Задача о перемещении точки.
Пусть v = v ( t ) скорость прямолинейного движения точки, заданная на некотором промежутке времени [t 1 ; t 2]. При этом пусть v ( t )>0. Как выразится длина пути, пройденного точкой за данный промежуток времени?[5]
Обозначим координату движущейся точки в момент t через S ( t ). Тогда, так как движение при v >0 происходит только в положительном направлении (или иначе, т. к. S ( t ) – функция возрастающая, ввиду того, что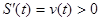 
), то искомое расстояние будет выражаться числом S ( t 2 )- S ( t 1 ). С другой стороны S ( t ) есть первообразная функции v ( t ) ( 
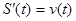). Таким образом вычисление длины пути, пройденного точкой за данный промежуток времени, сводится к отысканию первообразной S ( t ) функции v ( t ), т. е. к интегрированию функции v ( t ).
|
|
|
Разность S ( t 2 )- S ( t 1 ) называют интегралом от функции v ( t ) на отрезке [t 1 ; t 2] и обозначают так:
.
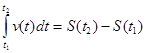Импульс силы.
Пусть на тело массой m в течение времени t действует какая-то сила F ( t ). Найти количество движения тела при заданной зависимости силы от времени за промежуток времени [t 1 ; t 2].
Как известно из физики второй закон Ньютона в импульсном представлении выражает уравнение
ΔР=FΔt.
Произведение P = mv ( t ) массы на скорость называется «количеством движения». Так как скорость тела зависит от времени, то за промежуток времени [t 1 ; t 2] искомое количество движения может быть найдено так: Р ( t 2 )- Р ( t 1 ) . С другой стороны Р ( t ) есть первообразная функции F ( t ). Таким образом вычисление количества движения тела за данный промежуток времени, сводится к отысканию первообразной Р( t ) функции F ( t ).
Разность P ( t 2 )- P ( t 1 ) называют интегралом от функции F ( t ) на отрезке [t 1 ; t 2] и обозначают так:
.
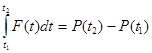Величина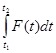 
называется также «импульсом силы» за время [t 1 ; t 2]. Словесная формулировка результата: изменение количества движения равно импульсу силы.
Количество электричества.
Представим себе переменный ток, текущий по проводнику. Вычислим количество электричества, протекающего за интервал времени [a; b] через сечение проводника. Если бы сила не менялась со временем, то изменение количества электричества q равнялось бы произведению I(b-a). Пусть задан закон изменения I= I( t) в зависимости от времени. Тогда количество электричества, протекающего за интервал времени [a; b], равно q( b)- q( a). С другой стороны на малом промежутке времени можно считать силу тока постоянной и равной I( t), а dq= I( t) dt, следовательно, вычисление количества электричества за данный промежуток времени, сводится к отысканию первообразной функции I( t).
|
|
|
Разность q ( b )- q ( a ) называют интегралом от функции I ( t ) на отрезке [a ; b] и обозначают так:
.
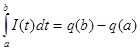Вытекание воды из сосуда.
Дата добавления: 2019-07-15; просмотров: 222; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!