Глава 5. ИНТЕГРИРОВАНИЕ ОБЫКНОВЕННЫХ

ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Рассмотрим обыкновенное дифференциальное уравнение вида

, (5.1)

где х – аргумент, у – неизвестная функция х, f – некоторая заданная функция переменных х и у.

Это уравнение называется уравнением первого порядка, поскольку в него входит только первая производная неизвестной функции .

Из курса математического анализа известно, что уравнение вида (5.1) может иметь бесконечное множество решений. Чтобы решение было единственным, необходимо задать еще значение у в некоторой точке х₀, т.е. необходимо дополнительное условие вида

, (5.2)

где у₀ – некоторое заданное значение.

Условие вида (5.2) обычно называют начальным условием, а задачу определения функции у(х), удовлетворяющей уравнению (5.1) и начальному условию (5.2) – задачей Коши.

Путем решения задачи Коши можно определить, каким образом при будет изменяться функция , удовлетворяющая уравнению (5.1), если при .

Для иллюстрации рассмотрим простейший пример. Пусть есть одномерное движение точки с постоянной скоростью ; обозначим у – пройденный путь, – время. Тогда по определению скорости

Это – частный случай уравнения (5.1). Общее решение этого уравнения – 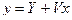. Однако положение точки в конкретном случае зависит не только от скорости его движения , но и от его начального положения (рис. 5.1). Если задать начальное условие в виде (5.2), получим и хорошо знакомое выражение перемещения для равномерного прямолинейного движения:

Решение задачи Коши.

Вспомним определение производной. Производная функции в точке обозначается

и определяется выражением

Это значит, что при очень маленьких

, (5.3)

причем чем меньше , тем точнее выполняется это равенство.

Это означает, что при малых

Из условия (5.2)

Следовательно,

Обозначим 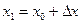и . Поскольку

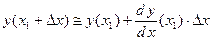а также

получим

И так далее. Обозначив , , получим

, (5.4)

Это выражение может применяться при любом . Пусть необходимо вычислить при некотором заданном . Величина называется шагом интегрирования. Будем повторять вычисления по формуле (5.4) до тех пор, пока не выполнится условие . Имея значения и можем определить величину в промежуточной точке ( ) методом линейной интерполяции, описанном в главе 1:

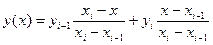Таким образом, можно получить значения при любом сколь угодно большом .

Этот метод получил название метода Эйлера. При его использовании необходимо учитывать, что величина должна быть достаточно малой, чтобы обеспечить точность вычисления на каждом шаге (5.4) (условие точности) и не допускать неконтролируемого накопления ошибок вычислений (условие устойчивости). Строгий анализ этих условий довольно сложен и требует некоторой математической подготовки. Однако для практического использования можно применить простой прием: вычислить сначала при некоторой малой величине шага интегрирования, затем повторить вычисление при величине шага интегрирования, вдвое меньшей. Если разница между полученными таким образом двумя значениями не превышает заданную точность, можно считать, что условия точности и устойчивости выполнены.

На аналогичном принципе основаны более точные и сложные методы Рунге-Кутты. На практике для решения задачи Коши наиболее часто применяется так называемый метод Рунге-Кутты с четырьмя членами. Если известно значение 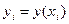, то величина при использовании метода Рунге-Кутты с четырьмя членами определяется следующим образом.

Сначала вычисляют четыре вспомогательные величины

Затем величина определяется по формуле

Если задача Коши сформулирована не для скалярной функции , а для системы дифференциальных уравнений относительно неизвестных функций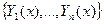

(5.5)

а граничное условие задано в виде

(5.6)

то решение получается точно такими же методами Эйлера и Рунге-Кутты с той лишь разницей, что вместо скалярных функций и в точно таких же выражениях стоят вектор-функции

Это позволяет решать задачи Коши для уравнений не первого, а более высоких порядков. Рассмотрим, например, уравнение второго порядка (при этом правая часть может быть функцией не только аргумента и значения неизвестной функции, но и значения ее производной)

. (5.7)

Поскольку это уравнение второго порядка, начальные условия должны задавать начальные значения не только самой функции , но и ее первой производной (соответственно, для уравнения -го порядка начальные условия задают значения функции и всех ее производных до -го порядка включительно), т.е.

. (5.8)

Введем следующие обозначения

Тогда задача Коши для вектор-функции запишется в виде

Начальные условия запишутся в виде

Полученная запись является частным случаем (5.5)-(5.6). Следовательно, для решения этой задачи Коши можно совершенно аналогично использовать описанные выше методы Эйлера и Рунге-Кутты.

Решение краевых задач

Обыкновенное дифференциальное уравнение определяет общий вид решения, а конкретное решение из общего вычленяется заданием начальных условий. Количество условий равно порядку уравнения.

Рассмотрим уравнение (5.7). Для конкретизации общего решения, соответствующего изучаемой проблеме, надо задать два условия. Если они заданы в виде (5.8), то сформулированная таким образом задача получила название задачи Коши. Однако может случиться так, что в соответствии с реальными задачами из общего решения (5.7) надо выделить частное решение заданием не начальных условий (5.8), а двух условий несколько другого вида, в которых только одно задает значение функции в начальный момент, а второе – в конечный момент 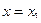. Таким образом, два условия, конкретизирующие общее решение (5.7) в этом случае имеют вид

(5.9)

Определение решения уравнения (5.7) при условиях (5.8) получило название краевой задачи.

Для ее решения воспользуемся методами, изложенными в предыдущих разделах. Рассмотрим задачу Коши для уравнения (5.7) при начальных условиях

(5.10)

Зададим какое-то произвольное начальное значение и будем решать задачу Коши (5.7), (5.10) методом Эйлера или методом Рунге-Кутты до 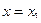. Получим значение 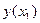, естественно, зависящее от заданного ранее значения , т.е. . Очевидно, что функция не выражена в виде какой-то формульной зависимости (в т.н. аналитической форме), а получается из численного решения задачи Коши (5.7)–(5.10). Здесь читателю рекомендуется вспомнить определение понятия «функция»: в случае функции одной переменной это закон, устанавливающий соответствие одному числу (аргументу) другое число (значение функции). Именно такой закон и устанавливает решение задачи Коши (5.7)–(5.10) при любом заданном значении . В случае, когда функция задана не в виде формульных зависимостей, говорят, что функция является неявно заданной. 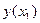Скорее всего, задавая какое-то произвольное значение , мы получим величину , отличающуюся от , т.е. первое условие (5.10) выполняется точно, а вот второе условие – с ошибкой, равной . Таким образом, заданной в начале величине соответствует ошибка . Введем обозначение неявно заданной функции

Будем решать нелинейное уравнение

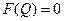. (5.11)

По виду оно совершенно ничем не отличается от (4.1), где в данном случае 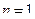. Следовательно, его можно решать описанными в главе 4 методами дихотомии или Ньютона.

Если для решения (5.11) избран метод Ньютона, для его использования надо уметь определять величину производной

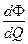Если бы функция была задана в виде формульной зависимости, это можно было бы сделать, воспользовавшись знаниями, полученными при изучении курса математического анализа. Как же быть, когда функция задана неявным образом? Никаких принципиальных затруднений это не вызывает. Предположим, что мы произвольным образом задали какое-то начальное значение (т.н. нулевое приближение). Получить формульное выражение мы не можем, но для использования метода мы не можем, но для использования метода Ньютона нам нужно не столько это формульное выражение, сколько значение производной в точке , а его приближенное выражение можно получить из выражения (5.3). Выберем малую (относительно ) величину и в полном соответствии с (5.3) вычислим приближенное значение в точке по формуле

где значения и получают из численного решения задачи Коши (5.7)–(5.10) соответственно при и .

Аналогичным образом решаются краевые задачи для систем линейных уравнений и уравнений более высокого, чем второй, порядка.

Контрольные вопросы к главе 5:

1. Лаборатория располагает 100 мг стонция-90 для проведения радиологических экспериментов. Однако вследствие радиоактивного распада количество стронция уменьшается. Изменение его массы удовлетворяет уравнению

где – время в годах, 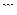– масса стронция-90. В начальный момент времени = 100 мг. Определить массу стронция через 28 лет (период полураспада стронция-90 – 28.8 лет) путем решения поставленной задачи Коши методом Эйлера с шагом интегрирования 2 года.

Ответы на контрольные вопросы:

Глава 1.

1. Полином 3-й степени

2. Интерполяционный полином: , .

3. Ответ:

Глава 2.

1. Параметры аппроксимирующей линейной зависимости: , т.е. сама аппроксимирующая линейная зависимость – .

Глава 3.

2. =0, следовательно, эти векторы взаимно перпендикулярны.

3. градиент Ф в точке – вектор . Следующее приближение – .

Глава 4.

2. 9.5 лет

Глава 5.

1. 50.1 мг

Рекомендуемая литература

1. Березин И.С., Жидков Н.П. Методы вычислений (в 2-х томах), Т.1 / И.С.Березин, Н.П.Жидков– М.: ГИФМЛ, 1962. – 464 с.

2. Березин И.С., Жидков Н.П. Методы вычислений (в 2-х томах), Т.2 / И.С.Березин, Н.П.Жидков– М.: ГИФМЛ, 1962. – 620 с.

3. Современные численные методы решения обыкновенных дифференциальных уравнений / Под ред. Дж.Холла, Дж.Уатта. М.: Мир, 1979. 312 с.

4. Фаддеев Д. К. , Фаддеева В. Н. Вычислительные методы линейной алгебры/ Д. К. Фаддеев, В. Н. Фаддеева – М.: Физматгиз. 1960. – 658 с.

5. Гилл Ф., Мюррей У., Райт М. Практическая оптимизация/ Пер. с англ. / Ф.Гилл, У.Мюррей, М.Райт – М. : Мир, 1985. – 509 с.

Дата добавления: 2019-02-22; просмотров: 158; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 56

Мы поможем в написании ваших работ!