Глава 2. АППРОКСИМАЦИЯ ФУНКЦИЙ

⇐ ПредыдущаяСтр 3 из 6Следующая ⇒

Метод линейной интерполяции позволяют приближенно вычислить значение функции в промежуточной точке между двумя узловыми точками. Возможность использования метода основывается на предположении, что резкие нелинейные изменения этой функции между узловыми точками отсутствуют. Принципиальный вид функциональной зависимости при этом неизвестен.

Однако на практике часто возникает необходимость найти функцию, принципиальный вид которой известен, но неизвестны параметры, входящие в эту зависимость. Например, зависимость коэффициента диффузии D от температуры Т имеет вид

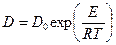. (2.1)

Здесь R = 8.314 Дж/(моль·К) – универсальная газовая постоянная. D₀ и Е – неизвестные константы (т.н. частотный фактор и энергия активации). Если найти значения D₀ и Е, то тем самым будет полностью определена функция 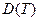. Предположим, что в двух опытах совершенно точно измеряются значения D и Т, т.е. из первого опыта известны точные значения Т₁ и D₁, а из второго – Т₂ и D₂ . Тогда, взяв натуральные логарифмы от правой и левой частей уравнения (2.1) можно записать два равенства

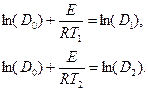
Это – система двух линейных уравнений относительно неизвестных Е и 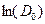. Решив ее, получим

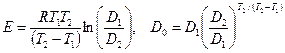Таким образом, зависимость коэффициента диффузии от температуры определена, если есть два совершенно точных измерения. Очевидно, впрочем, что на практике совершенно точные измерения ни для температуры, ни для коэффициента диффузии невозможны. Однако, если методика эксперимента отлажена, можно получить не 2, а большее число значений D при различных Т. Предположим, получено N значений коэффициента диффузии при N различных значениях Т. Обозначим эти значения температуры 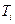(i = 1,…,N), а соответствующие значения коэффициента диффузии – 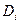. Вследствие неточности измерений, как бы ни была проведена на графике кривая зависимости 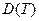, она не пройдет точно через все точки 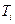, т.е. при любых параметрах Е и 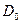вычисленные значения 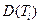не равны измеренным значениям D_i во всех точках 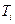, i = 1,…,N . Можно попытаться найти такие параметры Е и 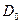, что суммарное отклонение всех значений 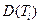от D_i невелико. Это отклонение равно 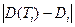. Таким образом, необходимо найти такие параметры Е и 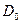при которых функция

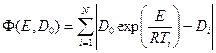
имеет минимум.

Если ошибки измерения 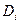независимы и распределены по нормальному закону, то наилучшая оценка параметров Е и 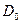соответствует наименьшему значению не суммы абсолютных величин отклонений, а суммы квадратов отклонений, т.е. наиболее точная оценка параметров Е и 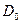соответствует минимуму функции

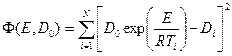Определяя таким образом зависимость коэффициента диффузии от температуры, получаем кривую, которая не проходит в точности через все заданные точки, а является наиболее близкой к ним среди всех кривых заданного типа (т.е. соответствующих функциональной зависимости (2.1)). Определение функции, наиболее близкой к заданным значениям в некоторых фиксированных точках из всех функций заданного типа, называется построением аппроксимирующей зависимости или решением задачи аппроксимации.

Выше рассмотрена задача аппроксимации для определения зависимости коэффициента диффузии от температуры. Эта задача является двухпараметрической, поскольку она сводится к определению двух неизвестных параметров: Е и D₀. Очевидно, что в общем случае количество неизвестных параметров может быть различным. Представим задачу аппроксимации в общем виде. Предположим, что некоторая физическая величина Y является функцией n переменных: Х₁, …, Х _n. Вид функциональной зависимости Y от Х₁, …, Х _n известен, однако в выражение этой функции входят m неизвестных параметров: Р₁, …, Р _m, т.е.

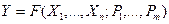(2.2)

В рассмотренном в начале главы 2 примере общая форма зависимости (2.2) принимает вид (2.1), при этом n = 1, Х₁ = Т; m = 2, Р₁ = Е, Р₂ = D₀.

Конкретные значения переменных Х₁, …, Х _n определяют точку в n-мерном пространстве. Это пространство может быть одномерным, как в рассмотренном в начале главы случае. Рассмотрим водный раствор n различных независимых компонентов при фиксированных температуре и давлении. Конкретное состояние раствора определяется значениями концентраций этих компонентов: С₁, …, С _n. Таким образом, множество состояний раствора n независимых компонентов является n-мерным пространством, а каждое конкретное состояние этого раствора – точкой этого пространства.

Предположим, что известны значения величины Y в N точках n-мерного пространства:

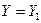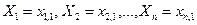
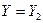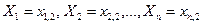
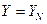при

… …

при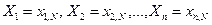

Необходимо найти такие значения параметров Р₁, …, Р _m, при которых функция

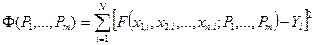
принимала наименьшее значение.

Таким образом, сформулирована задача аппроксимации в общем виде. Необходимо найти значения Р₁, …, Р _m , при которых функция Ф имеет минимум. Пусть этот минимум достигается при 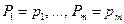. Предположим, что Ф является дифференцируемой при этих значениях параметров Р₁, …, Р _m. Это означает, что при малых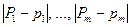

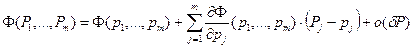где

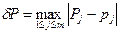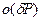– бесконечно малая более высокого порядка, чем 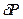, т.е.

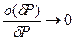при 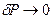. (2.3)

Необходимыми условиями минимума Ф при 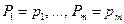являются равенства

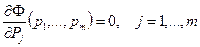. (2.4)

Покажем это. Пусть, например, при каком-нибудь j

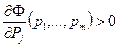Согласно условию (2.3) можно выбрать такие d Р < 0, что

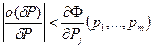Рассмотрим следующие значения параметров:

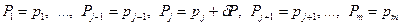При этих значениях параметров

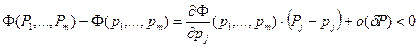Это означает, что значение 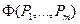меньше 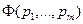, но по условию 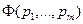– наименьшее значение Ф. Таким образом, предположение, что хотя бы одна из частных производных Ф не равна нулю, является ложным.

Записав уравнения (2.4), получили m уравнений относительно m неизвестных: р₁, …, р _m. Возможно, что уравнения (2.4) имеют несколько решений, т.е. существует М (где М – целое число, М>1) наборов р₁, …, р _m , при которых выполняются уравнения (2.4). Тогда из всех полученных решений этих уравнений методом перебора определяется то, при котором функция Ф принимает наименьшее значение.

Рассмотрим следующий пример такого способа определения параметров аппроксимирующей функции. Зависимость удельной изобарной теплоемкости органических веществ от температуры описывается степенной функцией

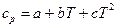, (2.5)

где с_р – удельная теплоемкость; a, b, c – неизвестные параметры аппроксимирующей функции.

Экспериментальным путем определены значения с_р при N значениях Т: 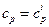при , 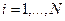. По этим результатам приближенных измерений надо найти неизвестные параметры аппроксимирующей зависимости вида (2.5).

Функция Ф в рассматриваемом случае имеет вид

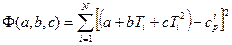Необходимые условия минимума функции запишутся в виде

Суммируя отдельно все члены выражения в квадратных скобках, получим:

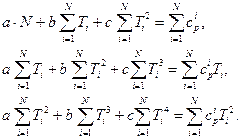
Получили систему 3 линейных уравнений относительно трех неизвестных: a, b и c. Это систему уравнений можно решить, например, методом Гаусса или методом Крамера. Известно, что если определитель этой системы не равен нулю, то решение существует и единственно. Тогда необходимое условие минимума Ф становится и достаточным условием.

В рассмотренном случае задачу аппроксимации можно решить аналитически, если, например, записать явные выражения всех определителей в методе Крамера. Возможность получения аналитического решения задачи обусловлена относительно простым видом аппроксимирующей зависимости (2.5). На практике такая возможность появляется далеко не всегда, и для решения задачи аппроксимации приходится пользоваться приближенными итерационными методами. Поскольку задача аппроксимации сведена к задаче минимизации функции, зависящей от нескольких параметров, эти методы называют методами параметрической оптимизации, т.е. методами определения оптимального (в данном случае – минимального) значения функции нескольких параметров и значений самих параметров, при которых достигается оптимум этой функции.

Контрольные вопросы к главе 2:

1. Для очистки сточных вод предприятия решено было использовать старый пруд-отстойник. В процессе работы предприятия в пруде с течением времени стали накапливаться осадки. Предприятие работает в стационарном режиме, поэтому скорость осадконакопления постоянна. Следовательно, толщина слоя осадков 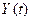должна быть линейной функцией времени: 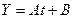. Аппроксимировать зависимость 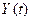линейной функцией 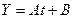, если произведено 4 измерения толщины слоя осадков: в начале работы предприятия и затем каждый следующий год.

t, годы	0	1	2	3
Y, дм	1	1.5	2.5	4

Построить график аппроксимирующей зависимости и отложить на нем точки, в которых значения функции известны.

Глава 3. МЕТОДЫ ОПТИМИЗАЦИИ

Операции над векторами.

Введем систему декартовых координат в трехмерном пространстве: x, y, z. Радиусом-вектором или просто вектором точки с координатами X, Y, Z будем называть направленный отрезок прямой, начальной точкой которого является начало координат, а концом – точка с координатами X, Y, Z (рис. 3.1).

Векторные величины будем в дальнейшем обозначать символами со стрелками сверху, например: 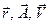. Величины X, Y и Z будем называть компонентами радиуса-вектора. Векторы совпадают тогда и только тогда, когда у них равны все три компоненты. Соответствие вектора 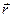его компонентам X, Y и Z будем обозначать следующим образом

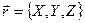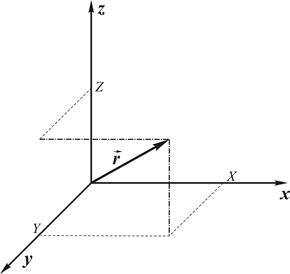
Рис. 3.1. Вектор в трехмерном пространстве. Чтобы получить его координаты X и Y, конечную точку вектора проецируют на плоскость ху (штрих-пунктирная линия), а на этой плоскости – на оси х и у (тонкие пунктирные линии). Для определения координаты 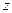конечную точку радиуса-вектора проецируют на плоскость yz (штрих-пунктирная линий), а на ней – на ось 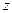(тонкая пунктирная линия.

Длину вектора 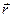будем обозначать 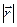или r. Из теоремы Пифагора (рис. 3.2) следует, что

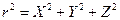. (3.1)

Это непосредственно следует из последовательного рассмотрения двух прямоугольных треугольников: ОАВ и ОАС (рис. 3.2).

Рассмотрим два вектора: и 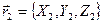. Сумму векторов 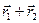определим следующим образом. Перенесем вектор 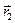параллельно самому себе так, чтобы его начало совпало с концом вектора 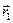. Тогда конец перенесенного вектора 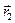является конечной точкой вектора суммы 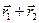. Проведем через конечные точки векторов 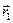и 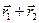плоскости, перпендикулярные оси х (рис 3.3). Расстояние между этими плоскостями равно Х₂. Следовательно, компонента вектора 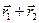по оси х равна Х₁ + Х₂ . Аналогично этому можно показать, что компоненты вектора 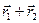по осям y и z равны, соответственно, 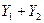и .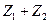

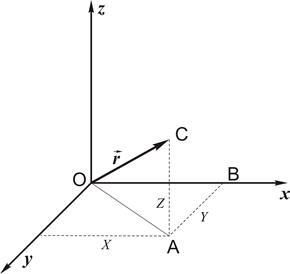
Рис.3.2. Длина радиуса-вектора

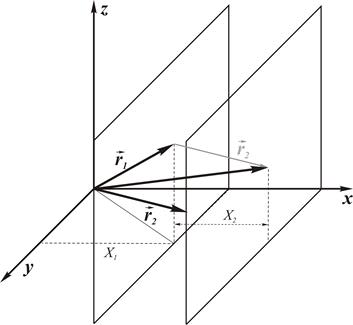
Рис. 3.3. Сумма векторов

Разностью векторов 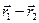называется вектор, сумма которого с вектором 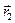равна 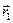. Очевидно, что при этом

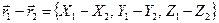Произведением вектора 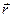с компонентами X, Y и Z на скалярную величину a будем называть вектор a 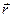, имеющий длину 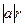и направленный вдоль вектора так, что направления векторов 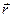и a 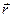совпадают при a>0 и противоположны при a<0. Проекции конечной точки вектора a 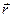на оси координат x, y и z будут равны, соответственно, а X, а Y и а Z. Это легко проверить, проведя три плоскости, каждая из которых проходит через вектор 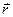и одну из осей координат. Таким образом при произведении вектора на скаляр каждая из компонент этого вектора умножается на скаляр.

Скалярным произведением двух векторов 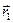и 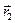называется скалярная величина, равная произведению длины вектора 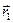на проекцию вектора 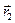на вектор 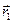или произведению длин этих векторов, помноженному на косинус угла между ними. Операцию скалярного произведения векторов 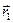и 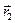будем обозначать 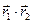. Проведем плоскость, проходящую через векторы 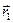и 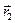(рис. 3.4).

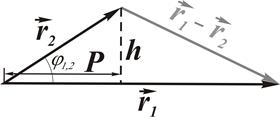
Рис. 3.4. Скалярное произведение векторов

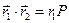, где Р – проекция 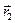на вектор 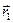. Из определения разности векторов следует, что вектор, проведенный из конечной точки 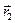в конечную точку 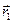, равен разности 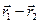. Квадрат длины вектора 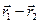равен

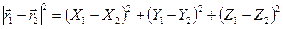. (3.2)

По теореме Пифагора из рис. 3.4 следует

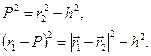
Вычтем второе равенство из первого. Получим

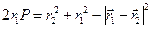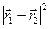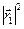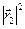Подставим в это уравнение выражение (3.2) для и выражения вида (3.1) для и . Получим

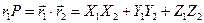По определению

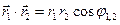, (3.3)

где j_1,2 – угол между векторам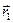и и .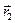

Отсюда следует, что

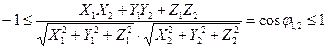Градиентный метод

Рассмотрим функцию F(x, y, z). Градиентом функции F в точке с координатами x, y, z называется вектор с компонентами

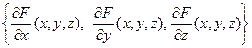Градиент функции F обозначается следующим образом: 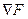или .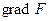

Рассмотрим вектор единичной длины 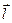с компонентами 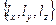. Проведем прямую, проходящую через точку с координатами 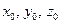параллельно вектору 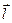. Так как длина вектора равна единице, .

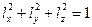Обозначим 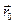радиус-вектор точки с координатами 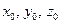. Тогда радиус-вектор любой точки на этой прямой можно представить в виде 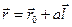(рис. 3.5), где а – любое число. Это значит, что координаты любой точки этой прямой имеют вид

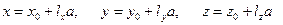. (3.4)

Рассмотрим, каким образом изменяется функция F вдоль этой прямой. Подставив выражения для координат точек прямой, получим

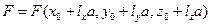
Выражение (3.4) является определяющим для всех точек прямой при 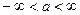. Рассмотрим значение а = А и определим, насколько точка переместится вдоль прямой при увеличении параметра a на D а. Значению а = А соответствует точка прямой с координатами

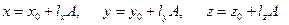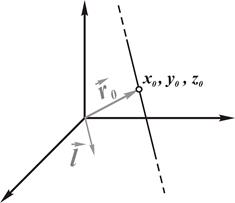
Рис. 3.5. Прямая, проходящая через заданную точку параллельно заданному вектору

Значению a = А + D а соответствует точка с координатами

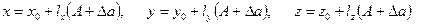Рассмотрим разницу значений координат x, y и z, полученных для а = А и a = А + D а. Получим, что координата х увеличилась на l_xDа, у увеличилась на l _уDа, а z – на l_zDа. По теореме Пифагора расстояние между двумя точками на прямой, соответствующими значениям а = А и a = А + D а , равно

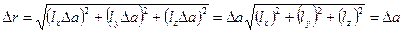Разность значений функции F в этих двух точках равна

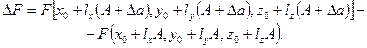
По определению производной сложной функции

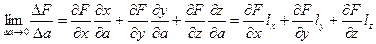(3.5)

Получено выражение производной функции F в направлении рассмотренной прямой. Эту величину обозначим

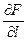Например, если l_x = 1, l _у = 0 и l_z = 0, в соответствии с (3.4) получим прямую, параллельную оси х. В этом случае

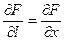Из выражения (3.5) следует, что производная функции F по направлению 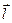– это скалярное произведение градиента F на вектор :

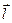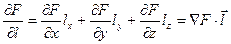Согласно (3.3), т.к. длина вектора 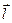равна единице,

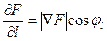где j _l – угол между вектором 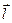и вектором градиента F.

При малых Dа, согласно определению производной,

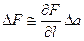Так как 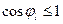, для фиксированного Dа величина DF максимальна при j _l = 0, т.е. приращение функции по какому-либо направлению максимально, если это направление совпадает с направлением градиента этой функции. И наоборот, наиболее быстро функция убывает при 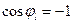, т.е. при j _l = – p , иными словами, вдоль направления, обратного направлению градиента.

Таким образом, направление наиболее быстрого уменьшения функции F – это направление вектора с компонентами

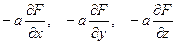где а – любое положительное число (поскольку согласно определению произведения вектора 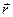на скаляр а вектор 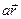направлен вдоль вектора .

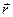Ранее в данном курсе рассматривались только трехмерные векторы, т.е. векторы в трехмерном пространстве, имеющие три компоненты. Аналогично тому, как это делалось для вектора в трехмерном пространстве введем понятие вектора в n-мерном пространстве (где n – любое положительное целое число), как объекта, однозначно соответствующего упорядоченному набору n компонент. Условие соответствия, как и в случае трехмерных векторов запишем в виде .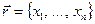

Для n-мерных векторов можно определить операции суммы и разности векторов, произведения вектора на скаляр и скалярного произведения двух векторов точно так же, как и в случае трехмерных векторов. Пусть есть два n-мерных вектора: 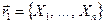и 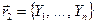. Суммой этих векторов будем называть вектор

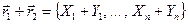Разностью векторов 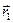и 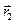будем называть вектор

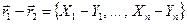
Произведением вектора 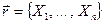на скаляр а будем называть вектор

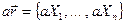Скалярное произведение n-мерных векторов 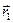и 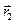определим по аналогии со скалярным произведением векторов в трехмерном пространстве

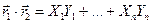Длиной n-мерного вектора 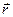с координатами 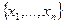будем называть величину

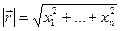Если F – функция n переменных, ее градиент является n-мерным вектором

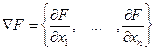Точно так же, как для функции трех переменных, в случае n переменных можно показать, что функция F(x₁, … , x_n) быстрее всего убывает в направлении антиградиента F. Это означает, что при малых положительных фиксированных Dа

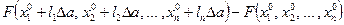
принимает наименьшее значение, если

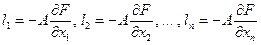где

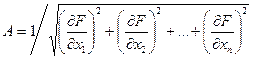В качестве примера рассмотрим функцию трех переменных

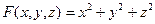Эта функция – квадрат расстояния точки до начала координат. Очевидно что минимальное значение F = 0 эта функция принимает при 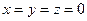. Точно так же очевидно, что быстрее всего функция F убывает вдоль радиуса-вектора этой точки, т.е. прямой, проходящей через точку и начало координат. Рассмотрим теперь вектор градиента F: 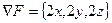. Это означает, что вектор градиента направлен вдоль радиуса-вектора точки. Вектор антиградиента имеет противоположное направление, т.е. он лежит на прямой, соединяющей точку с началом координат и направлен в сторону начала координат. Таким образом, на конкретном примере можно убедиться, что направление наибыстрейшего уменьшения функции – вектор антиградиента этой функции.

В приведенном примере рассматривалась очень простая функция. На практике часто приходится определять точку минимума значительно более сложных функций, причем не всегда даже можно определить аналитически компоненты градиента этой функции. В рассмотренном примере вектор антиградиента направлен из любой точки в точку минимума функции. В общем случае это не так. Например, смещение из исходной точки 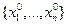вдоль антиградиента на расстояние Dа приведет в точку

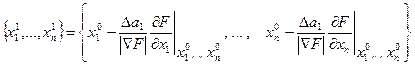где

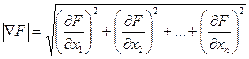Первая точка была исходным, т.е. нулевым, приближением, что было обозначено ее верхним индексом. Верхний индекс координат новой точки равен единице. Это означает, что новая точка является следующим, т.е. первым приближением. Как было показано выше, при фиксированном достаточно малом Dа₁ в этом случае разность 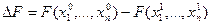будет наибольшей. Следует еще раз подчеркнуть, что это выполняется лишь при достаточно малых Dа, поскольку особые свойства градиента функции в некоторой точке как направления наибыстрейшего возрастания функции были доказаны лишь для достаточно малой окрестности этой точки. Если выбранная величина Dа₁ окажется слишком большой, величина 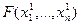может оказаться даже большей, чем 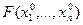(рис. 3.6а). Это связано с тем, что вектор градиента может меняться от точки к точке, и направление градиента в точке 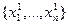может не совпадать с направлением градиентом в точке .

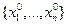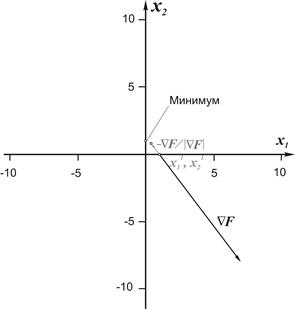
а б

Рис. 3.6. Пример минимизации функции двух переменных методом градиента

а) первый шаг; б) второй шаг

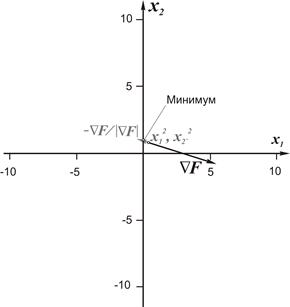
Чтобы проиллюстрировать это, рассмотрим простейший пример. Пусть n = 2 и 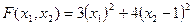. Из вида самой функции ясно, что она больше либо равна нулю, и что наименьшее ее значение есть нуль, которому функция равна в точке (0, 1). В качестве начального приближения рассмотрим точку с координатами: 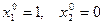. В этой точке F = 7. Определим выражения компонент градиента функции:

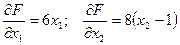Тогда подставляя значения х₁ и х₂ в точке 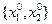в выражения компонент вектора градиента, получим 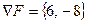. При этом

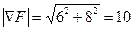Сместимся из 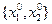вдоль антиградиента на расстояние 1. Получим

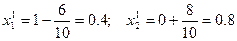Подставив значения х₁ и х₂ в точке 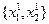в выражения компонент градиента, получим 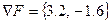. Представив двумерное пространство в виде плоскости, отложим на этой плоскости векторы градиента в точках нулевого и первого приближений (рис. 3.6 б). Можно отметить, что эти два вектора отличаются по направлению.

В точке 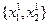F = 0.8, т.е. при перемещении в направлении, обратном направлению градиента, функция F действительно существенно уменьшилась. Было показано, что функция уменьшается быстрее всего вдоль направления, обратного ее градиенту. Может показаться, что определив в некоторой точке вектор градиента и перемещаясь в направлении, обратном этому вектору, мы достигнем минимума функции. Однако, как только что показал рассмотренный пример, вектор градиента в общем случае меняется от точки к точке. Вследствие этого, если переместиться вдоль направления, противоположного градиенту, на слишком большое расстояние, может оказаться даже, что значение 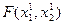будет больше 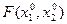. В самом деле, предположим, что Dа₁ = 5. Тогда 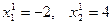. В этом случае 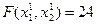. Следовательно, для уменьшения значения функции 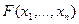путем перемещения вдоль направления, противоположного градиенту, необходимо руководствоваться условием

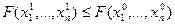. (3.6)

Процесс приближения к минимуму функции F можно продолжить аналогичным образом. Для этого, перейдя от нулевого приближения к первому, необходимо заново вычислять вектор градиента, чтобы вдоль антиградиента перейти от первого приближения ко второму.

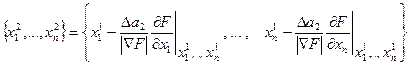Как и при определении первого приближения, величина Dа₂ должна быть достаточно малой, чтобы по крайней мере выполнялось условие, аналогичное (3.6).

Такую процедуру минимизации функции F можно продолжать и дальше, переходя от m-го приближения к (m+1)-му с помощью следующих соотношений

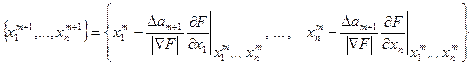(3.7)

при условии, что величина Dа _m₊₁ удовлетворяет условию

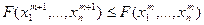, (3.8)

которое выполняется при достаточно малом Dа _m₊₁ .

В результате такой процедуры на каждом приближении определяются не точные, а приближенные n-мерные координаты минимума функции F, причем на каждом следующем приближении эти координаты определяются все точнее (поскольку выполняется условие (3.8)). Однако в общем случае нельзя ожидать, что на каком-то приближении координаты минимума будут определены совершенно точно. Вследствие этого возникает вопрос, на каком шаге следует завершить процедуру приближенного определения координат минимума, т.е. какое приближение следует считать достаточно точным. В некоторых случаях, как, например, в рассмотренных в данном разделе примерах, минимальное значение функции F известно совершенно точно. Тогда критерием точности приближенного определения координат минимума функции F может быть условие

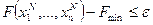где N – номер приближения, на котором следует завершить процедуру; F_min – известное минимальное значение функции F; e – заданная точность.

Как правило, F_min неизвестна. Однако в точке локального минимума функции градиент этой функции должен быть равен нулю. Отсюда следует, что

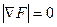. (3.9)

Следовательно, остановить процедуру приближенного вычисления минимума функции F можно исходя из того, насколько точно выполняется условие (3.9). Обозначим 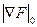абсолютную величину градиента функции F в начальном приближении. Тогда критерием точности выполнения условия (3.9) может быть неравенство

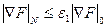, (3.10)

где 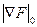– абсолютная величина градиента в N-ом приближении; e₁ – заданная точность.

Такой критерий является характеристикой того, насколько N-ое приближение 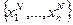находится ближе к точке минимума функции F, чем начальное приближение .

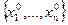Описанная процедура получила название градиентного метода поиска минимумов функций.

Следует отметить, что эффективность и быстрота определения минимума функции с помощью градиентного метода (т.е. количество приближений, необходимых для определения минимума) могут существенным образом зависеть от удачного выбора начального приближения. Это, в первую очередь, связано с тем, что функция в исследуемой области параметров может иметь несколько минимумов (рис. 3.7). В связи с такой возможностью следует пояснить различие между понятиями локального минимума и общего (или глобального) минимума. Локальным минимумом в n-мерных координатах называется радиус-вектор 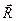точки с координатами 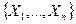такой, что существует малая ее окрестность, в которой все значения функции больше, чем значение функции в этой точке. Это означает, что точка 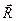является локальным минимумом, если существует положительное d такое, что для любой другой точки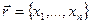 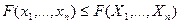, если 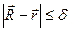. Как видно из рис. 3.8, функция может иметь несколько локальных минимумов. Тот локальный минимум, в котором функция принимает самое меньшее значение во всей рассматриваемой области значений (т.е. наименьшее из значений во всех локальных минимумах) называется общим (или глобальным) минимумом.

Если необходимо определить градиентным методом общий минимум, то начальное приближение необходимо выбрать в той области, где снижение функции возможно лишь к этому минимуму (а не к какому-либо другому локальному минимуму). Для пояснения этого рассмотрим функцию одной переменной

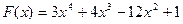изображенную на рис. 3.7. Сначала найдем минимумы этой функции аналитически с помощью методов, изложенных в курсе математического анализа. Для этого найдем производную F(x):

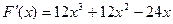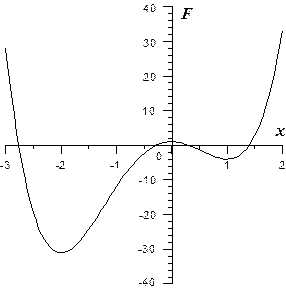
Рис. 3.7. График функции, имеющей два локальных минимума

Эта функция равна нулю при Х₁ = –2, Х₂ = 0 и Х₃=1. Поскольку в этих точках вторая производная F(x) не равна нулю, они являются точками локальных экстремумов (минимумов или максимумов) функции F(x) . Поскольку F(x) – полином четвертой степени с положительным коэффициентом при старшем члене, Х₁ и Х₃ являются точками локальных минимумов, а Х₂ – точка локального максимума. F(X₁) = – 31, F(X₃) = – 4. Таким образом функция F(x) имеет два локальных минимума в точках Х₁ и Х₃, причем .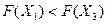

А теперь для определения общего минимума F(x) воспользуемся градиентным методом. В случае одной переменной вектор градиента имеет единственную компоненту – 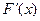. Обозначим начальное приближение х⁰. Тогда первое приближение определяется по формуле

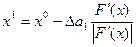где Dа₁ – некоторое положительное число.

Если производная 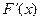отрицательна, то при малых Dа₁ следующее приближение находится справа от предыдущего, а если положительна, то слева.

Предположим, что 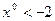. Тогда при достаточно малых Dа с помощью градиентного метода мы постепенно приближаемся слева к точке минимума х = – 2. Если 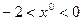, то на всем этом интервале 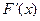положительна, и при достаточно малых (чтобы не перескочить через минимум) величинах Dа₁ мы с помощью градиентного метода постепенно приближаемся справа к точке минимума х = – 2. Однако легко проверить, что при 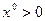мы с помощью градиентного метода точно также справа или слева будем приближаться к точке другого локального минимума: х = 1.

Таким образом, если в рассмотренном примере необходимо определить градиентным методом не просто какой-нибудь локальный минимум, а общий минимум, следует выбирать начальное приближение из условия .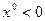

Для понимания сущности градиентного метода при минимизации функций одной или двух переменных очень удобно пользоваться механической аналогией. Представим, что график функции F(x) на рис. 3.7 – верхняя граница какого-либо тела. В точке с координатой х⁰ опустим на эту границу маленький шарик. Под действием силы тяжести этот шарик покатится вдоль границы вниз к какому-нибудь из минимумов. Именно это движение шарика вдоль границы под действием силы тяжести и имитирует градиентный метод.

Следовательно, удачный выбор начального приближения для градиентного метода имеет большое значение в тех случаях, когда минимизируемая функция имеет несколько локальных минимумов, и для определения наименьшего из них (общего минимума) необходимо задать начальное приближение так, чтобы целью минимизации был именно этот локальный минимум.

Контрольные вопросы к главе 3:

1. Найти сумму 2 векторов: 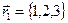и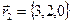

2. Найти скалярное произведение двух векторов: 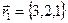и 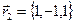и убедиться, что эти векторы взаимно перпендикулярны.

3. Необходимо определить градиентным методом минимум функции

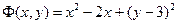
Задано начальное приближение: 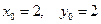. Определить градиент Ф в этой точке и найти следующее приближение, смещаясь вдоль антиградиента на расстояние 0.5. Убедиться, что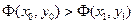

Дата добавления: 2019-02-22; просмотров: 274; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 Следующая ⇒

Мы поможем в написании ваших работ!