Методы решения нелинейных уравнений

⇐ ПредыдущаяСтр 5 из 6Следующая ⇒

Часто при обработке экспериментальных данных возникает необходимость решать нелинейные уравнения. Так, например, проницаемость горных пород (параметр, характеризующий их способность пропускать газы и жидкости) нельзя измерить непосредственно. Одна из методик экспериментального определения проницаемости (метод затухания импульса) заключается в следующем. Образец исследуемой породы цилиндрической формы с изолированными боковыми поверхностями соединяют с резервуаром, заполненным газом. Затем давление газа в резервуаре скачком повышают на величину 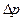. За счет фильтрации газа через породу давление в резервуаре постепенно снижается. Чем больше проницаемость, тем быстрее снижается давление. 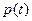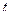В опытах измеряются величины (где – давление, – время). Проницаемость определяется по их значением из решения нелинейного уравнения

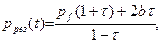(4.5)

где

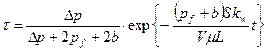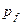– исходное давление в резервуаре, 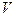– объем резервуара, 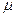– динамическая вязкость газа, 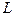– длина образца, 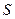– его поперечное сечение, 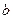– константа Клинкенберга, 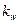– проницаемость.

Обозначим 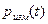измеренное значение давления в резервуаре в момент 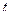. Тогда в опыте величина проницаемости определяется из решения нелинейного уравнения

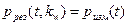. Совершенно очевидно, что получить аналитическое решение (4.5) нереально. И единственная возможность решить задачу – воспользоваться методами вычислительной математики.

Метод дихотомии

Рассмотрим простейший метод решения нелинейного уравнения вида (4.1) с одним неизвестным ( 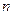=1), т.е.

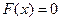Предположим, что уравнение (4.1) имеет решение х = Х, т.е. 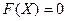Будем считать, что при этом 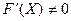. Пусть для определенности 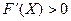(все последующие рассуждения практически аналогичным образом применимы и к случаю ). Если производная функции в точке х = Х положительна, то функция в этой точке монотонно возрастает. Это значит, что существует такая окрестность 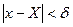точки х = Х (d-окрестность), что 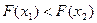если 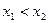( 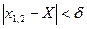). Выберем произвольное значение 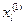из левой части d-окрестности точки х = Х . Тогда 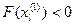. Выберем произвольное положительное число Dх< d и к величине будем прибавлять по Dх до тех пор, пока не получим 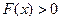(рис. 4.1). Полученное значение х обозначим 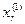. Таким образом мы определили отрезок 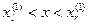, на котором функция возрастает, на левой границе отрицательна, а на правой – положительна. Необходимо теперь приближенно определить точку на отрезке, в которой эта функция равна нулю. Определим середину этого отрезка

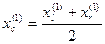
и вычислим .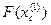

Если 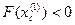, то

т.е. определим новый отрезок, правая граница которого совпадает с правой границей предыдущего отрезка, а левая граница – середина предыдущего отрезка. Точно так же на новом отрезке функция возрастает, на левой границе отрицательна, а на правой – положительна.

Если же 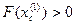, то

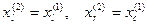т.е. определим новый отрезок, левая граница которого совпадает с левой границей предыдущего отрезка, а правая граница – середина предыдущего отрезка. И в этом случае на новом отрезке функция возрастает, на левой границе отрицательна, а на правой – положительна.

Следовательно, решение уравнения (4.1) находится на новом отрезке, причем если мы в качестве приближения к этому решению возьмем середину нового отрезка, это приближение будет отличаться от точного решения не больше, чем на величину

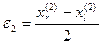Продолжим это процедуру. Определив на n-ом приближении отрезок 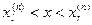, находим центр этого отрезка

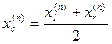
и вычисляем .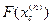

Если 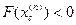, то

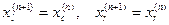а если 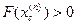, то

При этом длина отрезка на (n+1)-ом приближении равна

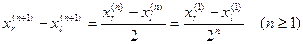Если в качестве приближенного решения (4.1) мы примем середину отрезка 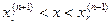, т.е. величину

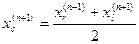то это приближение будет отличаться от точного решения не более, чем на половину длины отрезка:

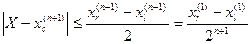Таким образом, увеличивая n, с помощью описанной процедуры можно определять решение (4.1) со сколь угодно высокой точностью. Этот метод получил название метода дихотомии.

Достоинством метода является его необыкновенная простота. Если в самом начале определить отрезок, на котором функция F(x) монотонно возрастает, а ее значения на границах этого отрезка имеют разные знаки, метод всегда позволяет получить решение нелинейного уравнения со сколь угодно высокой точностью (правда, метод следует несколько откорректировать, если на исходном отрезке содержится не один, а несколько корней уравнения). К безусловным недостаткам метода дихотомии следует отнести сложности определения исходного отрезка, однако в тех случаях, когда функция F(x) является монотонно возрастающей на всей числовой оси, эта задача существенно упрощается. И, разумеется, существенным ограничением в применении метода является то, что он может использоваться лишь для решения нелинейного уравнения с одним неизвестным.

Метод Ньютона

Рассмотрим несколько более сложный метод приближенного решения нелинейных уравнений вида (4.1). Выберем некоторое начальное приближение х⁽⁰⁾ и представим в этой точке функцию F(x) в виде линейной части многочлена Тейлора, т.е.

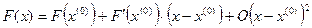Предположим, что точка с координатой х находится достаточно близко к начальному приближению х⁽⁰⁾ , так что членом О(х - х⁽⁰⁾)² как величиной второго порядка малости по (х - х⁽⁰⁾) в этом выражении можно пренебречь, т.е.

. (4.2)

Это соответствует приближенному представлению кривой F(x) в точке х⁽⁰⁾ в виде прямой, касательной к кривой F(x) в этой точке (рис. 4.2).

Предположив, что F(x) приближенно равна 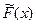, и приравняв 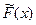к нулю, получим следующее приближение к решению уравнения (4.1):

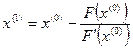Поскольку в общем случае кривая не совпадает с касательной к ней, х⁽¹⁾, конечно, не является решением (4.1), но, как видно из рис. 4.3, первое приближение х⁽¹⁾ находится ближе к точному решению, чем нулевое приближение х⁽⁰⁾ . Естественно найти аналогичным образом следующее приближение, которое еще ближе к точному решению, и т.д.

Обозначим n-ое приближение х⁽ⁿ⁾ . Тогда (n+1)-ое приближение определяется по формуле

. (4.3)

Таким образом, метод позволяет определять приближенное решение уравнения (4.1), которое с ростом n, казалось бы, все ближе и ближе к точному решению. Этот способ решения нелинейных уравнений получил название метод Ньютона.

Важным условием эффективности применения метода является то, что с ростом числа приближений можно сколь угодно близко подойти к точному решению Х. Это свойство называется сходимостью метода. Метод является сходящимся, если для любого, сколь угодно малого значения точности e существует такое приближение N, что при всех n > N выполняется неравенство 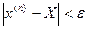. Например, метод дихотомии всегда является сходящимся. А вот практика использования метода Ньютона показала, что он в некоторых случаях сходящимся не является. Это, например, возможно, если решение уравнения является одновременно и точкой перегиба функции F(x) (рис. 4.4). Из рис. 4.4 видно, что при этом каждое следующее приближение «перескакивает» через точное решение, не приближаясь к нему все ближе, а, наоборот, все дальше и дальше отходя от него. В этом случае можно использовать модифицированный метод Ньютона, введя контроль сходимости. Для описания модифицированного метода обозначим, как и раньше, n-е приближение х⁽ⁿ⁾. Для определения (n +1)-го приближения получим сначала вспомогательную величину

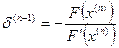затем вычислим

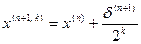где k - целое число, которое на данном приближении увеличивается на 1 от 0 до тех пор, пока не выполнится условие

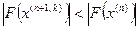Полученное значение х⁽ⁿ^+1,^k⁾ будем считать (n +1)-ым приближением, т.е. х⁽ⁿ⁺¹⁾ = х⁽ⁿ^+1,^k⁾.

Точность решения уравнения (4.1) методом Ньютона можно считать приближенно равной величине d⁽ⁿ⁺¹⁾.

Количество, приближений, необходимых для решения уравнения (4.1) с заданной точностью, зависит от удачного выбора начального приближения. Некоторая неопределенность такого выбора, основанная до некоторой степени на интуиции и индивидуальном опыте вычислителя, является недостатком метода. Но этот выбор представляет, как правило, гораздо меньше затруднений при решении практических задач, чем определение исходного отрезка в методе дихотомии. Отчасти вследствие этого метод Ньютона получил большее распространение. Однако гораздо большее преимущество метода Ньютона по сравнению с методом дихотомии состоит в том, что путем некоторого обобщения метод Ньютона можно использовать не только для решения отдельных уравнений, но и систем нелинейных уравнений относительно нескольких неизвестных.

Рассмотрим систему n нелинейных уравнений

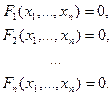(4.4)

относительно n неизвестных: х₁, …, х _n.

Совокупность значений {х₁, …, х _n} можно интерпретировать как точку в n-мерном пространстве с координатами х₁, …, х _n .

Выберем некоторое начальное приближение и обозначим его . Точно так же, как и в случае одного уравнения относительно одного неизвестного, представим все функции 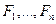системы (4.4) в виде линейных частей их многочленов Тейлора в начальном приближении (в точке n-мерного пространства с координатами ):

…

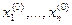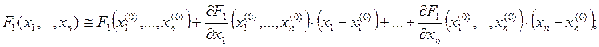
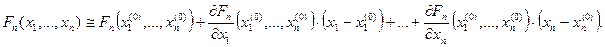Предположим, что решение системы уравнений (4.4) существует и единственно. Обозначим это решение 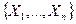. В этой точке все функции 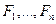должны быть равны нулю. Но мы приравняем к нулю не сами функции, а их линейные части, пользуясь тем, что линейные части приближенно равны самим функциям. Получим

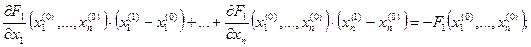
… (4.5)

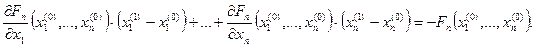
Система (4.5) – это система n линейных уравнений относительно неизвестных 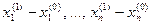. Эту систему уравнений можно решить, например, методом Гаусса. Поскольку начальное приближение 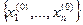известно, из решения системы линейных уравнений (4.5) получим следующее приближение решения исходной системы (4.4). Эту процедуру можно повторять и дальше, все точнее определяя приближенное решение системы нелинейных уравнений (4.4).

Очевидно, что, как и в случае решения одного уравнения, при решении системы уравнений метод Ньютона не всегда является сходящимся. Однако модификация метода для контроля сходимости осуществляется совершенно аналогично тому, как это делалось в случае решения одного уравнения.

Контрольные вопросы к главе 4:

1. Решить методом Гаусса систему линейных уравнений

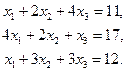
2. Потребности поселка в электроэнергии растут экспоненциально по времени и удовлетворяются за счет генераторов на дизельном топливе. Ежегодные поставки топлива составляют 5000 тонн в год. Первоначальные запасы составляли 10000 тонн. Потребность в топливе возрастает как 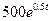тонн в год ( 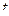– время в годах). Запасы топлива в поселке будут истощены при 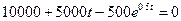. Решить уравнение методом дихотомии при начальном приближении 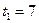лет с точностью 0.1 года.

3. Решить ту же задачу методом Ньютона

Дата добавления: 2019-02-22; просмотров: 170; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 Следующая ⇒

Мы поможем в написании ваших работ!