Глава 4. РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Системой алгебраических уравнений называется совокупность равенств вида
(4.1)
где 
– алгебраические выражения, не содержащие операторов дифференцирования и интегрирования, т.е.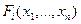 
– функции от 
переменных: 
( 
).
Например, пусть есть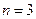 
и
В этом примере 
, и 
, 
, 
.
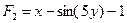Если ввести векторные обозначения
, 
,
т.е. F – n-мерный вектор с компонентами: , и х – также n-мерный вектор с компонентами: 
, то уравнение (4.1) можно записать в более компактной векторной форме
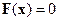. (4.2)
Обычно рассматриваются случаи, когда число уравнений в системе (4.2) равно числу неизвестных, т.е. размерности векторов F и х совпадают.
Решение систем линейных уравнений методом Гаусса.
В наиболее простом случае функции – линейные, т.е.
(4.3)
где 
– не зависящий от коэффициент, в двойном нижнем индексе которого первая часть – i – соответствует номеру функции (или номеру уравнения в системе уравнений (4.2)), а вторая часть – j – номеру неизвестного xj, в произведении с которым этот коэффициент входит в выражение линейной функции 
.
Таким образом, в линейном случае система уравнений (4.2) примет вид
или
(4.4)
Совокупность коэффициентов 
образует матрицу системы линейных уравнений (4.4):
,
а правые части – вектор
|
|
|
Решение системы (4.4) не изменится, если левую и правую части какого-либо из уравнений системы, например, первого умножить на постоянную величину 
. В этом случае матрица системы и вектор правых частей примут вид
, 
Точно так же решение не изменится, если правые и левые части какого-либо уравнения (например, первого) умножить на с и прибавить к соответствующим частям другого уравнения (например, второго). В этом случае матрица новой системы и вектор правых частей примут вид
, 
Таким образом, системы уравнений с матрицами 
и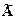 
и правыми частями 
и 
имеют одинаковые решения. На этом свойстве систем линейных уравнений основано их решение методом Гаусса. Пусть есть система уравнений вида (4.4). В ее матрице А в первом столбце есть хотя бы один коэффициент 
, не равный нулю. Если это не так, то система уравнений вообще не зависит от 
, т.е. число уравнений равно n, а число неизвестных меньше n. Следовательно, есть основание предположить, что в постановке задачи может содержаться ошибка. Будем считать, что в нашем случае это не так и хотя бы один коэффициент 
не равен нулю. Поменяем местами i-е уравнение с первым (очевидно, что от этого решение системы не изменится). Затем умножим обе части первого уравнения на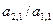 
и вычтем из второго уравнения, затем умножим на 
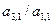и вычтем из третьего уравнения, и т.д. до n-го уравнения включительно. В результате получим новую систему уравнений, в которой матрица и вектор правых частей имеют вид
|
|
|
, 
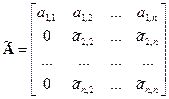Знак ~ означает, что эти величины – не те, что входили в исходную систему, а были получены в результате описанной выше процедуры. Теперь во втором столбце матрицы 
найдем хотя бы один коэффициент 
( 
!). Поменяем местами i-е уравнение со вторым. Затем умножим обе части 2-го уравнения на 
и вычтем из соответствующих частей третьего уравнения. Затем – на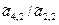 
и вычтем из соответствующих частей четвертого уравнения. И т.д., вплоть до n-го уравнения. Получим систему уравнений с матрицей вида
.
Можно отметить, что в первом случае получилась система уравнений с матрицей, в которой под первой строкой в первом столбце все коэффициенты равны нулю. Во втором случае получилась система, в которой помимо этого еще и во втором столбце ниже второй строки все коэффициенты равны нулю. Выберем 
( 
!) и повторим ту же процедуру для третьего столбца матрицы (не забывая, разумеется пересчитывать соответствующим образом компоненты вектора правых частей). И так далее – вплоть до n-го столбца. В результате в конце получим систему уравнений с матрицей и вектором правых частей вида
|
|
|
, 
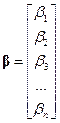
Все компоненты матрицы, стоящие под диагональными, равны нулю.
Из последнего уравнения сразу же получаем 
. Подставляем полученное значение 
во все остальные уравнения. Отсюда из предпоследнего уравнения – 
. Подставляем и это значение во все остальные уравнения, и из уравнения с номером n–2 получим 
. И так далее, пока не дойдем до первого уравнения.
Существенным преимуществом метода Гаусса является то, что его применение не требует совершенно никакой математической подготовки, и если размерность системы уравнений не слишком велика или систему уравнений не надо решать многократно, метод Гаусса вполне можно рекомендовать для применения из-за его простоты и надежности. Однако при необходимости решать системы уравнений, размерность которых достигает нескольких сотен, а то и тысяч, объем вычислений при их решении методом Гаусса становится чрезмерно большим. В этих случаях следует использовать более эффективные, но и требующие некоторых знаний по линейной алгебре методы, описанные в [1, 2, 3].
|
|
|
Дата добавления: 2019-02-22; просмотров: 136; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!