Глава 1. ИНТЕРПОЛЯЦИЯ ФУНКЦИЙ

Стр 1 из 6Следующая ⇒

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Российский химико-технологический университет имени Д. И. Менделеева»

В. И. Мальковский

Практическое руководство по вычислительной математике для построения инженерно-экологических моделей

Москва 2018

УДК 519.6:66.011:502

ББК 22.19:35.11; 30в6

Мальковский В. И.

Практическое руководство по вычислительной математике для построения инженерно-экологических моделей / В. И. Мальковский М.: РХТУ им. Д. И. Менделеева, 2018. – с. ISBN

Руководство содержит основные сведения по методам вычислений для решения наиболее часто встречающихся задач, возникающих при обработке экспериментальных данных или при проведении инженерных расчетов. Учебное пособие в минимальной степени касается математического обоснования приведенных в ней методов вычислений, основное внимание уделено их практическому применению при решении реальных задач.

Предназначена для аспирантов и студентов технических университетов, специализирующихся в области экспериментальных физико-химических исследований, химической технологии, экологии и природопользования.

УДК 519.6:66.011:502

ББК 22.19:35.11; 30в6

Учебное издание

Мальковский Виктор Иоаннович

Практическое руководство по вычислительной математике для

построения инженерно-экологических моделей

Редактор

Подписано в печать .18 г. Формат 60х84 1/16.

Бумага SvetoCopy. Отпечатано на ризографе.

Усл. печ. л. 2,27. Уч. изд. л. 2,44

Тираж 500 экз. Заказ
ОГЛАВЛЕНИЕ

	Предисловие	4
1.	Интерполяция функций	6
	1.1. Функция одной переменной	6
	1.2. Функция нескольких переменных	10
2.	Аппроксимация функций	12
3.	Методы оптимизации	18
	3.1. Операции над векторами	18
	3.2. Градиентный метод	22
4.	Решение алгебраических уравнений	33
	4.1. Решение систем линейных уравнений методом Гаусса	34
	4.2. Методы решения нелинейных уравнений	37
	4.2.1. Метод дихотомии	38
	4.2.2. Метод Ньютона	41
5.	Интегрирование обыкновенных дифференциальных уравнений	45
	5.1. Решение задачи Коши	46
	5.2. Решение краевых задач	49
	Рекомендуемая литература	52

ПРЕДИСЛОВИЕ

При проведении естественнонаучных исследований какого-либо объекта (процесса, системы, явления) одна из наиболее часто возникающих задач - определение функциональной зависимости неизвестной характеристики этого объекта от известных его параметров. Эту зависимость можно определить методами математического моделирования или экспериментальным исследованием. Для математического моделирования необходимость в знании вычислительных методов очевидна. Однако умение использовать эти методы может оказаться очень полезным и для экспериментаторов. Как правило, в опытах производится несколько измерений какой-либо величины при изменении одного из параметров эксперимента. Иногда по измеренным значениям требуется определить значения этой величины в промежуточных точках (задача интерполяции), иногда характер зависимости измеряемой величины от изменявшегося в ходе эксперимента параметра известен, однако эта зависимость включает неизвестные константы, которые надо определить по данным измерений (задача аппроксимации). В некоторых случаях неизвестная величина определяется в эксперименте косвенным путем, т.е. определяется не сама эта величина, а числовые параметры уравнения, из решения которого она определяется. При этом возможность получить аналитическое (т.е. в виде формулы) решение такого уравнения существует довольно редко. Часто необходимо определить параметры экспериментальной установки, при которых чувствительность измеряемой величины к вариациям изменяемого параметра позволит установить зависимость между ними с требуемой точностью. Решение всех этих задач требует знакомства со специальными математическими методами, совокупность знаний о которых принято назвать вычислительной математикой. Детальное знакомство с ней входит в программу подготовки математиков любого российского университета. Однако для практического использования методов вычислительной математики их углубленное изучение требуется не так уж часто. Во многих случаях для решения каких-то естественнонаучных задач вполне достаточно знания конкретных практических приемов, а строгое изложение доказательств их эффективности совершенно не требуется.

Чтобы оценить достоинства и недостатки такого сугубо утилитарного подхода к изучению методов вычислительной математики, уместно провести аналогию с советской и американской системами обучения водителей автотранспорта. В СССР на курсах вождения существенная часть времени отводилась изучению материальной части автомобиля и значительно меньшая – практическому вождению. В США знание водителями материальной части, по-видимому, никого не интересовало вообще, а обучение было сфокусировано почти целиком на правилах дорожного движения и практических навыках вождения.

Как оказалось, это позволяет вполне эффективно решить задачу обеспечения автотранспорта водителями. Правда, только до появления неисправностей и нештатных ситуаций.

Предлагаемое учебное пособие содержит описание практического применения основных математических методов, необходимых для решения типовых задач, возникающих при проведении естественнонаучных исследований. Как и в приведенной аналогии, этого вполне достаточно при решении многих типовых задач, но только до тех пор, пока исследователь не столкнется со специфической задачей или случаем, когда обычный метод оказывается непригодным. В таких не столь уж часто встречающихся случаях читатель может обратиться за помощью к специалисту по вычислительной математике или попробовать решить возникшую нештатную проблему самостоятельно с помощью указанных в списке литературы книг, где приведенные в данном учебном пособии методы изложены гораздо более детально и строго.

Глава 1. ИНТЕРПОЛЯЦИЯ ФУНКЦИЙ

Функция одной переменной

Исследования в области естественных наук часто сводятся к определению какой-либо функциональной зависимости, например, как изменяется во времени концентрации растворенного вещества в растворе в исследуемом процессе.

Эта функция может быть получена из результатов измерений или рассчитана методами математического моделирования. Предположим, что требуется определить функцию 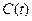в некотором интервале времени 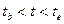(где t_b и t_e – начальное и конечное значения времени). Интервал (t_b , t_e) содержит бесконечное множество значений t. Предположим, что мы провели измерения или моделирующие расчеты и для дальнейшего использования полученных результатов записали их в память компьютера. Однако даже при очень большой памяти компьютера в ней может храниться только конечное количество числовых данных. Следовательно, надо найти способ, позволяющий хранить функцию 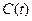в памяти компьютера в виде конечного набора значений 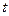и соответствующих значений 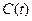. Задачей интерполяции является обратная операция – определение значения 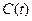в любой точке интервала 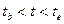по этому конечному набору пар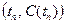

Представим функцию C(t) в виде ее значений в N точках 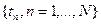, где 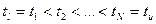, как это показано на рис.1.1. Эти точки назовем узловыми. Такое представление функции C(t) называется дискретным.

Будем считать, что между соседними узловыми точками резкие изменения величины С отсутствуют, так что график зависимости С(t) в промежутке между двумя узловыми точками представляет собой относительно гладкую кривую, близкую к отрезку прямой, проходящей через эти две точки. Тогда, начертив прямую, проходящей через соседние узловые точки, по графику прямой можно определить величину С при любом значении t между этими узловыми точками (рис. 1.2а). Таким образом вместо истинной зависимости С(t) получена приближенная зависимость с(t). Графиком с(t) является ломаная линия, которая в узловых точках пересекается с кривой С(t) (рис. 1.2а). Чем меньше расстояния между узловыми точками, тем ближе друг к другу графики с(t) и С(t).

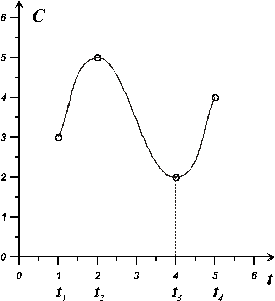
Рис. 1.1. Дискретное представление кривой ее значениями в 4 узловых точках. Расстояния между соседними точками могут быть неодинаковыми.

Такое определение непрерывной функции на отрезке от t_n до t_n₊₁ по ее известным значениям в граничных точках этого интервала (т.е. в t_n и t_n₊₁) называется линейной интерполяцией. Совокупность интерполяционных зависимостей на всех отрезках от n = 1 до n = N – 1 называется кусочно-линейной интерполяцией функции С(t) на множестве узловых точек .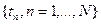

Значения интерполяционной линейной функции c(t) можно определить не только графически, но и по формулам линейных функций, определяющих величины c(t) между узловыми точками. Для этого получим выражения этих линейных функций. Рассмотрим пару соседних узловых точек: t_n и t_n₊₁ . В общем виде линейная функция одной переменной имеет вид

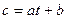т.е. эта функция полностью определяется двумя коэффициентами: а и b. Найдем эти коэффициенты по известным значениям С(t) в обеих узловых точках (в которых значения С и с совпадают).

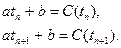
Отсюда

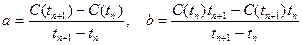Таким образом, при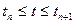

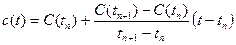. (1.1)

Такая кусочно-линейная интерполяция при 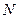=4 показана на рис. 1.2а.

а б

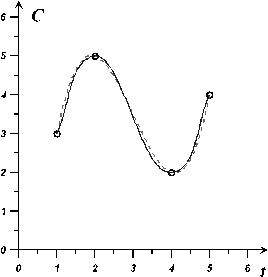
Рис. 1.2. Интерполяция функции по 4 точкам

Сплошная линия соответствует графику истинной функции, пунктиром показаны разные интерполяционные зависимости

а) кусочно-линейная интерполяция; б) интерполяция многочленом 3-й степени

Интерполяция не обязательно должна быть линейной. Если, например, рассмотреть не пары, а тройки соседних узловых точек 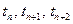, где 1 £ n £ N-2, то на отрезке 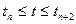зависимость C(t) можно приближенно определить в форме многочлена второй степени с₂(t) , значения которого в узловых точках 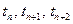равны значениям С(t). Такую интерполяцию называют квадратичной.

Если по двум узловым точкам осуществляется линейная интерполяция, по трем точкам – квадратичная, то можно предположить, что по всем N точкам можно подобрать полином степени N–1, значения которого во всех N точках совпадают со значениями функции C(t). Рассмотрим полином вида

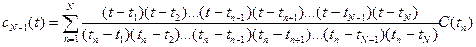. (1.2)

Этот полином является суммой N членов. Каждый член с номером 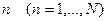представляет собой дробь, умноженную на коэффициент C(t_n). В числителе этой дроби стоит произведение всех 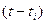, где i = 1, …, N за исключением i = n, а в знаменателе – произведение всех 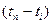, где i = 1, …, N за исключением i = n. Каждый член является многочленом степени N–1. Следовательно и сумма этих многочленов также является многочленом степени N–1. Каждая дробь в члене с номером n равна нулю во всех узловых точках за исключением 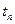, а в узле 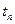равна единице. Таким образом, в узле 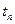равны нулю все члены суммы за исключением члена с номером n, равного C(t_n). Таким образом, вся сумма в узле 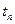равна C(t_n) . Следовательно, мы получили интерполяционный многочлен степени N–1, который во всех N узлах равен функции C(t). Представленный в виде (1.2) многочлен называется интерполяционным многочленом в форме Лагранжа. Пример такой интерполяции рассмотренной ранее функции по 4 точкам (т.е. 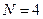) многочленом 3-й степени (поскольку 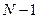=3) приведен на рис. 1.2б.

Выбирая достаточно большое количество узловых точек с достаточно малым расстоянием между соседними узлами, можно добиться того, что в промежутках между узловыми точками интерполяционный полином и интерполируемая функция принимают близкие значения, как на рис. 1.2б. Таким образом можно приближенно определить значения С(t) на всем промежутке между первым и последним узлами, т.е. на всем отрезке 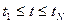. Можно попытаться с помощью интерполяционного полинома определить значения С(t) и за пределами этого отрезка. Такой способ определения С(t) (в отличие от расчета С(t) с помощью полинома 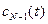во внутренних точках отрезка 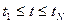) называется экстраполяцией. На первый взгляд возможность расчета значений неизвестной функции вне исследованного интервала t путем экстраполяции представляется весьма перспективной. Однако такой способ приближенного вычисления С(t) вне отрезка 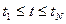с помощью функции 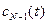может обеспечить удовлетворительную точность только в непосредственной близости от границ отрезка. По мере удаления от границ расхождение величин 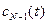и С(t) в общем случае становится все более и более значительным.

Вследствие простоты кусочно-линейной интерполяции этот способ часто используется на практике для приближенного вычисления функций по ее известным значениям в узловых точках.

Дата добавления: 2019-02-22; просмотров: 531; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 Следующая ⇒

Мы поможем в написании ваших работ!