Аналогия между поступательным и вращательным движениями
Между движением твердого тела вокруг неподвижной оси и движением отдельной материальной точки (или поступательным движением тела) существует тесная и далеко идущая аналогия. Каждой линейной величине из кинематики точки соответствует подобная величина из кинематики вращения твердого тела. Координате s соответствует угол φ, линейной скорости
v – угловая скорость w, линейному (касательному) ускорению а – угловое ускорение ε.
| Поступательное движение | Вращательное движение | ||||
| Кинематические характеристики движения | |||||
| Путь | S | м | Угол поворота | j | рад |
| Время | t | с | Период | Т | с |
| Скорость | v | м/с | Угловая скорость | w | рад/с |
| Ускорение | a | м/с2 | Угловое ускорение | e | рад/с2 |
| Поступательное движение | Вращательное движение | ||||
| Динамическиехарактеристики движения | |||||
| Масса | m | кг | Момент инерции | J | кг × м2 |
| Сила | F | Н | Момент силы | M | Н×м |
| Импульс | p | кг ×м/с | Момент импульса | L=J×w | кг ×м2/с |
| Второй закон Ньютона | F=ma; F=dp/dt | Уравнение динамики вращательного движения | M=J×e; M=dL/dt | ||
| Работа | dA=F× dS | Дж | Работа | dA=M×dj | Дж |
| Кинетическая энергия | EK=(mv2)/2 | Дж | Кинетическая энергия | EKВР=(Jw2)/2 | Дж |
| Мощность | N=FV | Вт | Мощность | N=М×w | Вт |
Поступательное движение можно рассматривать, как вращательное, с радиусом вращения, стремящимся к бесконечности, и угловой скоростью, стремящейся к нулю.
Момент инерции материальной точки и тела. Примеры вычисления момента инерции (цилиндр, шар).
Моментом инерции материальной точки относительно оси называется величина, равная произведению массы точки на квадрат расстояния до рассматриваемой оси: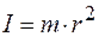 
.
Единица момента инерции - килограмм-метр в квадрате (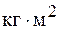 
). Моментом инерции твердого тела называют сумму моментов инерции материальных точек массой 
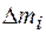, на которые можно разделить это тело, т. е. 
.
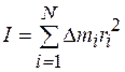Переходя к бесконечно малым массам dm, получаем 
На основании этой формулы можно рассчитать момент инерции любого тела.
В качестве примера получим формулу момента инерции однородного сплошного цилиндра относительно его оси (рис. 1).
Разобьем цилиндр на кольцевые слои толщиной dr. Все точки одного слоя будут находиться на одинаковом расстоянии r от оси. Объем такого слоя
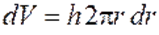, где h – высота цилиндра.
Поскольку цилиндр однороден, то масса dm выделенного слоя
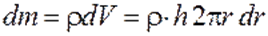, где r - плотность тела.
Получаем
.
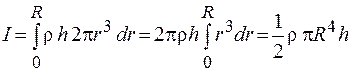Так как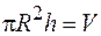 
- объем цилиндра, а 
- его масса, формулу приводим к виду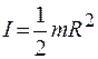 
. Эта формула применима для цилиндра любой высоты, в том числе и для диска.
Аналогично можно рассчитать моменты инерции и других однородных тел:
- для полого тонкостенного цилиндра относительно оси симметрии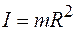 
, где R - радиус цилиндра;
- для прямого стержня относительно оси, перпендикулярной стержню и проходящей через его середину,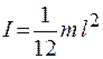 
, где l - длина стержня;
- для прямого стержня относительно оси, перпендикулярной стержню и проходящей через его конец,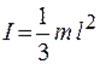 
, где l - длина стержня;
- для шара относительно оси симметрии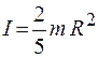 
, где R - радиус шара.
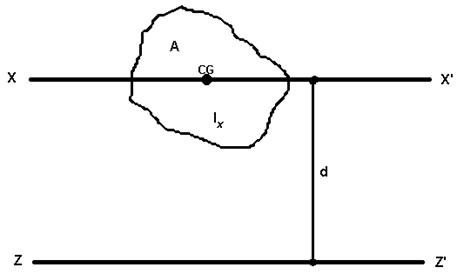
При нахождении момента инерции тел относительно оси, не проходящей через центр масс тела, вычисления значительно усложняются. Однако в подобных случаях можно воспользоваться теоремой Штейнера, которая формулируется следующим образом: момент инерции I относительно произвольной оси равен сумме момента инерции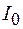 
относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния а между осями: 
.
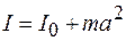Момент инерции твердого тела является мерой его инертности при вращательном движении.
Теорема Штейнера.
Теорема Штейнера применяется для установления связи между моментом инерции тел относительно двух параллельных осей .
Теорема Штейнера — момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями.
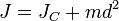
где
— известный момент инерции относительно оси, проходящей через центр масс тела,
— искомый момент инерции относительно параллельной оси,
— масса тела,
— расстояние между указанными осями.
Вывод теоремы
Момент инерции, по определению:
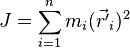
Радиус-вектор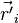 
можно расписать как разность двух векторов:
,
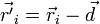где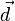 
— радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:
Вынося за сумму 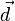, получим:
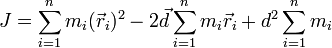
Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю:
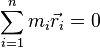
Тогда:
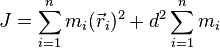
Откуда и следует искомая формула:
,
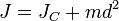где — известный момент инерции относительно оси, проходящей через центр масс тела.
Пример применения
Момент инерции стержня относительно оси, проходящей через его центр и перпендикулярной стержню, (назовём её осью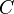 
) равен
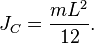
Тогда согласно теореме Штейнера его момент относительно произвольной параллельной оси будет равен
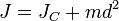
где — расстояние между искомой осью и осью 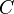. В частности, момент инерции стержня относительно оси, проходящей через его конец и перпендикулярной стержню, можно найти положив в последней формуле 
:
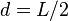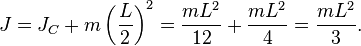
Пересчёт тензора инерции
Теорема Гюйнеса — Штейнера допускает обобщение на тензор момента инерции, что позволяет получать тензор относительно произвольной точки из тензора 
относительно центра масс. Пусть 
— смещение от центра масс, тогда
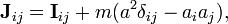
где
— вектор смещения от центра масс, а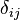 
— символ Кронекера.
16. Кинетическая энергия вращающегося тела.
Кинетическая энергия - величина аддитивная. Поэтому кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек, на которые это тело можно мысленно разбить:
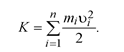
Если тело вращается вокруг неподвижной оси z с угловой скоростью ω, то линейная скорость i-й точки vi = ωRi, R, - расстояние до оси. Следовательно:
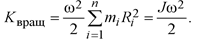
Сопоставив формулы, можно увидеть, что момент инерции тела J является мерой инертности при вращательном движении, так же как масса m - мера инерции при поступательном движении.
В общем случае движение тввердого тела можно представить в виде суммы двух движений – поступательного со скоростью ύc и вращательного с угловой скоростью ὡ вокруг мгновенной оси, проходящей через центр инерции этого тела
Кполн. =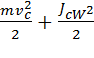 
Здесь 
- момент инерции относительно мгновенной оси вращения, проходящей через центр инерции.
17. Гироскоп. Гироскопический эффект. Прецессия гироскопа
Гироскоп – прибор, имеющий свободную ось вращения и способный реагировать на изменение углов ориентации тела, на котором он установлен. При вращении гироскоп сохраняет свое положение неизменным. Гироскопы представляют собой вращающиеся с высокой частотой твердые тела. Ось вращения гироскопа может изменять свое направление в пространстве. Свойствами гироскопа обладают вращающиеся артиллерийские снаряды, винты самолетов, роторы турбин. Простейший пример гироскопа – волчок или хорошо всем известная детская игрушка юла. Тело, вращающееся вокруг определенной оси, которая сохраняет положение в пространстве, если на гироскоп не действуют какие-то внешние силы и моменты этих сил. При этом гироскоп обладает устойчивостью и способен противостоять воздействию внешней силы, что во многом определяется его скоростью вращения. Например, если мы быстро раскрутим юлу, а потом толкнем ее, она не упадет, а продолжит вращение. А когда скорость волчка упадет до определенного значения, начнется прецессия – явление, когда ось вращения описывает конус, а момент импульса волчка меняет направление в пространстве.
Гироскопическим эффектом называется явление сохранения неизменности своего направления в пространстве быстровращающимся осесимметричным твердым телом.
Гироскопический эффект свойственен небесным телам, артиллерийским снарядам, роторам турбин, устанавливаемых на судах, винтам самолетов и т.п.
Прецессия гироскопа
Прецессия — явление, при котором момент импульса тела меняет своё направление в пространстве.
Если к оси шарнирно закрепленного в точке О гироскопа (рис. 92) прикрепить пружину и тянуть за нее вверх с силой F, то ось гироскопа будет перемещаться не в направлении силы, а перпендикулярно к ней, вбок. Это движение называется прецессией гироскопа под действием внешней силы.
Рис.92
Опытным путем можно установить, что угловая скорость прецессии зависит не только от величины силы 
(рис.92), но и от того, к какой точке оси гироскопа эта сила приложена: с увеличением и ее плеча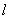 
относительно точки закрепления О скорость прецессии увеличивается. При этом оказывается, что чем сильнее раскручен гироскоп, тем меньше угловая скорость прецессии при данных и .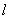
Гармонические колебания (механические) и их характеристики. Дифференциальное уравнение гармонических колебаний. Связь вращения и колебаний. Уравнение колебаний в комплексной форме.
Механическое гармоническое колебание - это прямолинейное неравномерное движение, при котором координаты колеблющегося тела (материальной точки) изменяются по закону косинуса или синуса в зависимости от времени.
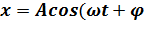0 ),
где x – смещение колеблющейся величины от положения равновесия;
А – амплитуда колебаний;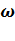 
= 2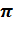 
/Е = 2 
– круговая (циклическая) частота;
v = 1| T – частота; T – период колебаний;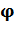 
0- начальная фаза ; 
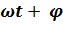0- фаза колебаний в момент t.
Круговая частота колебаний
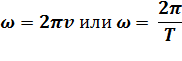
где v и T - частота и период колебаний.
Дифференциальное уравнение гармонических колебаний материальной точки:
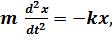или 
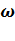+ 2 x = 0,
где m - масса точки; k - коэффициент квазиупругой силы ( k = m 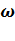2 ).
Дата добавления: 2019-02-22; просмотров: 804; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!