Как получить уравнение движения?

Допустим, в какой-то момент времени мы знаем все параметры, определяющие состояние системы – например, скорости и координаты, — а также их производные по времени. Тогда мы можем рассчитать эти параметры и для момента времени, отстоящего от начального на малый промежуток времени. Если мы выберем малый, но конечный промежуток времени б t, мы можем приближенно оценить состояние системы в любой момент времени. Для получения точного уравнения движения нужно определить функцию, описывающую процесс: если временной шаг б t выбран достаточно малым, то приближенно вычисленные характеристики системы будут лежать к этой функции очень близко.

Для каждой области физики существуют свои уравнения движения

В классической механике эту функцию, в первую очередь, выполняют законы Ньютона. Их дополняют закон тяготения и кинематические законы, связывающие перемещение, скорость и ускорение. Так, второй закон Ньютона – это уравнение движения материальной точки массой m, связывающий силу F, приложенную к точке, и ускорение a, которое точка вследствие этого приобрела:

 

Уравнение движения материальной точки:
F = dp/dt
т. е. скорость изменения импулься тела равна действующей силе. Эта формула -- непосредственное следствие определения импульса p = m*v и второго закона Ньютона F = m*a. Действительно, дифференцируя обе части определения импульса p = m*v, имеем: dp/dt = m*dv/dt = m*a = F.

Уравнение динамики поступательного движения тела: ma=

где m – масса тела, a(вектор)– его ускорение,

суммаF(i-тое) – сумма всех действующих на тело сил.

Основное уравнение динамики вращательного движения твердого тела: I e = M,где I– момент инерции твердого тела, относительно оси вращения, e – его угловое ускорение, М – суммарный момент сил, действующий на тело относительно данной оси.

 

Границы применимости классического способа описания движения частиц:Законы движения Ньютона действуют только в ИСО (инерциальных системах отсчета), относятся к материальным точкам.

5. Преобразова́ния Галиле́я

Преобразова́ния Галиле́я — в классической механике (механике Ньютона) и нерелятивистской квантовой механике преобразования координат и скорости при переходе от одной инерциальной системы отсчета (ИСО) к другой . Термин был предложен Филиппом Франком в 1909 году. Преобразования Галилея опираются на принцип относительности Галилея, который подразумевает одинаковость времени во всех системах отсчета («абсолютное время»).

Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для скоростей, малых по сравнению со скоростью света в вакууме и в ограниченном объёме пространства. Для скоростей вплоть до порядка скоростей движения планет в Солнечной системе (и даже бо́льших), преобразования Галилея приближенно верны с очень большой точностью.

Если ИСО S' движется относительно ИСО S с постоянной скоростью u{\displaystyle u\ } вдоль оси x {\displaystyle x\ }, а начала координат совпадают в начальный момент времени в обеих системах, то преобразования Галилея имеют вид:

x =x’ +ut;

y = y’;

z = z’;

t = t ’;

или, используя векторные обазначения:

t = t ’;

(последняя формула остается верной для любого направления осей координат).

Из этих преобразований следуют соотношения между скоростями движения точки и её ускорениями в обеих системах отсчета:

Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для малых скоростей {\displaystyle u\ll c}u « c (много меньше скорости света).

Достаточно продифференцировать {\displaystyle {\vec {r}}} в формуле преобразований Галилея, приведенной выше, и сразу же получится приведенная в том же параграфе рядом формула преобразования скорости.

Рассмотрим преобразование произвольного сдвига начала отсчета на вектор _0,

где радиус-вектор какого-то тела A в системе отсчета K обозначим за {\displaystyle {\vec {r}}} {\displaystyle {\vec {r}}}, а в системе отсчета K' — за 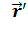{\displaystyle {\vec {r'}}},

₀ = ₀ ( t ) , = ( t ),

тогда в любой момент времени

= ₀ +

и в частности, учитывая

₀ = ₀ (t + ₀ (t),

имеем:

₀ ( t ) +

₀ (t +  +   ₀ + = ⁰ + ,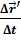

 

 

Силы в механике.

В механике обычно имеют дело с тремя основными видами сил: силой тяжести, силой упругости и силой трения.

 

Закон всемирного тяготения. Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния r между ними:

где G = 6,67∙10^–11 м³/кг∙с² – гравитационная постоянная.

Закон всемирного тяготения справедлив для точечных, а также сферически симметричных тел. Приближенно он выполняется для любых тел, если расстояние между ними значительно больше их размеров.

 

Сила тяжести. Одним из проявлений закона всемирного тяготения является сила тяжести. Сила тяжести направлена к центру Земли и на поверхности Земли равна:

F = mg,

где ускорение свободного падения Здесь масса Земли равна а ее радиус

Вблизи поверхности Земли ускорение свободного падения равно g = 9,8 м/с².

 

 

Сила, с которой тело действует на горизонтальную опору или подвес, называется весом тела По третьему закону Ньютона с той же по модулю силой опора или подвес действует на тело; эта сила называется реакцией опоры При неподвижной опоре или подвесе эта сила равна силе тяжести Следует помнить, что эти силы приложены к разным телам (рис. 3).

Рис. 3. Вес тела и реакция опоры

Если опора или подвес двигается с некоторым ускорением, то сила давления со стороны тела (то есть вес тела) изменяется.

В частности, если опора движется с ускорением направленным против силы тяжести, то вес тела обращается в нуль. Такое состояние называют невесомостью. Состояние невесомости испытывает космонавт в космическом корабле.

 

Сила упругости.

Рис. 4. Сила упругости

Изменение формы или размеров тела называется деформацией. Деформации бывают упругими и пластичными. При упругих деформациях тело восстанавливает свою форму и размеры после прекращения действия силы, при пластичных – нет. При упругих деформациях справедлив закон Гука: величина деформации пропорциональна вызывающей ее силе:

Fвнешн = –Fупр = kx.

Коэффициент k называется жесткостью.

Сила трения.

Силы, действующие между поверхностями соприкасающихся твердых тел, называются силами сухого трения. Они всегда направлены по касательной к соприкасающимся поверхностям.

Сила трения покоя – величина непостоянная, она растет по модулю вместе с внешней силой от нуля до некоторого максимального значения F_{тр max}. Сила трения покоя равна по модулю и противоположна по направлению проекции внешней силы, направленной параллельно поверхности соприкосновения его с другим телом.

Если внешняя сила больше F_{тр max}, то возникает движение. Силу трения в этом случае называют силой трения скольжения. Экспериментально доказано, что сила трения скольжения пропорциональна реакции опоры:

Fтр max = μN.

Коэффициент трения μ зависит от материалов, из которых изготовлены соприкасающиеся тела, и не зависит от размеров соприкасающихся поверхностей.

Сила трения скольжения всегда направлена против относительного движения тела.

При движении в жидкости или газе возникает сила вязкого трения. При вязком трении нет трения покоя. Сила вязкого трения значительно меньше силы сухого трения и также направлена в сторону, противоположную относительной скорости тела. Зависимость от модуля скорости может быть линейной F = –βυ или квадратичной F = –αυ².

---

Дата добавления: 2019-02-22; просмотров: 700; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!