Квазиупругая сила. Период колебаний пружинного, математического и физического маятников.

 

Если сила не является по своей природе упругой, но подчиняется закону F = -kх, то она называется квазиупругой силой.

Получим уравнение пружинного маятника. Учтем в записи второго закона Ньютона, что

тогда

                 

- дифференциальное уравнение точки, совершающей колебательное движение (дифференциальное уравнение пружинного маятника).

Решение дифференциального уравнения:

- уравнение колеблющейся точки (уравнение колеблющейся пружины).

- собственная частота колебаний.

 

Периоды колебаний математического и физического маятников

Математический маятник - материальная точка, подвешенная на невесомой нерастяжимой нити, и совершавшая колебания в вертикальной плоскости под действием силы тяжести. Материальная точка - тело, масса которого сосредоточена в центре масс и размерами которого в условиях данной задачи, можно пренебречь.

Математический маятник при колебаниях совершает движение по дуге окружности радиуса . Его движение подчиняется законам вращательного движения.

Основное уравнение вращательного цветения запишется в виде

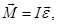(1)

М – момент сил, I – момент инерции, ε – угловое ускорение.

                                                  

Равнодействующая сил и равна .

Из треугольника АВС

      т.е.        

таким образом, колебания математического маятника происходят под действием квазиупругой силы - силы тяжести.

Тогда (1) запишется в виде (2)

Знак минус учитывает, что векторы и имеют противоположные направления (угол поворота можно рассматривать, как псевдовектор углового смещения , направление вектора определяется по правилу правого винта, из-за знака минус направлен в противоположную сторону).

Сократив в (2) на m и получим

При малых углах колебаний α = 5 ÷6° , , получим

Ввода обозначения

получим дифференциальное уравнение колебаний математического маятника

                   Его решение:          

- уравнение математического маятника.

из которого видно, что угол α изменяется по закону косинуса. α₀ - амплитуда, ω₀ - циклическая частота, φ₀ - начальная фаза.

- период колебаний математического маятника

Физический маятник - твердое тело, колеблющееся под действием силы тяжести вокруг неподвижной горизонтальной оси, не проходящей через центр тяжести тела, называемой осью качания маятника.

Основное уравнение – вращательного движения для физического маятника запишется в виде

При малых углах колебаний и уравнение движения имеет вид

Тогда положив

получим - дифференциальное уравнение физического маятника.

- период колебаний физического маятника

Приравняв Т_физ = Т_мат:

следовательно, математический маятник с длиной

имеет такой же период колебаний, как и данный физический маятник. - приведенная длина физического маятника - это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.

 

---

Дата добавления: 2019-02-22; просмотров: 622; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!