Инструкция по выполнению задания

⇐ ПредыдущаяСтр 9 из 9

1. В заданном графе G = (X, V) (рисунок 1) удалить указанные ребра (дуги) и новом графе G' найти все минимальные доминирующие множества (МДМ).
Ребро (дуга), которую необходимо удалить (Х4,Х5), (Х1,Х2)

Рисунок 1

Решение

Описываем каждую вершину с помощью дизъюнкции самой вершины и вершин, из которых она достижима. Например для

и составим конъюнкцию таких выражений для всех вершин.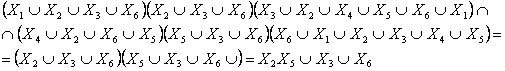

Таким образом МДМ1 = {Х2, Х5}, МДМ2 = {Х3}, МДМ3 = {Х6}.

2. В заданном графе G = (X, V) (рисунок 2) удалить указанные ребра (дуги) и новом графе G' найти все максимальные независимые множества (МНМ).
Ребро (дуга), которую необходимо удалить (Х4,Х5), (Х1,Х2)

Рисунок 2

Решение

Описываем каждое ребро (дугу) дизъюнкцией отрицаний и производим конъюнкцию всех дизъюнкций. Например ребро (Х2, Х1) описываем как и т.д.
Получим

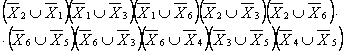
Производим упрощение.

Откуда из первой группы следует:
МНМ1 = {Х3}, МНМ2 = {Х6}, МНМ3 = {Х1, Х5}, МНМ4 = { Х1, Х4}.

Задания:

1. Перечислите все максимальные независимые множества графа G, показанного на рисунке, а также найти число независимости.

2. Составить список всех максимальных независимых множеств графа приведенного на рисунке. (Обратить внимание на симметрию)

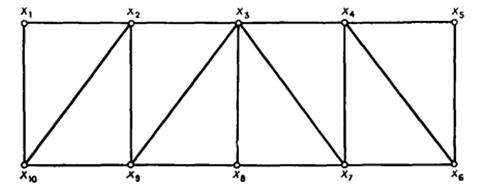
3. Найти доминирующие множества по рисунку.

4. Найти максимально независимые множества по рисунку.

Порядок выполнения работы:

1. Изучить инструкцию по выполнению задания

2. Выполнить задание.

3. Оформить отчет.

Содержание отчета:

1. Тема.

2. Цель.

3. Задачи.

4. Материальное обеспечение.

5. Практическое задание.

Вопросы для самоконтроля:

1. Какое множество вершин графа называется независимым?

2. Дайте определение доминирующего множества?

3. Дайте определение понятию ядро графа?

Практическая работа № 12

Тема: Решение задач по теории графов. Нахождение кратчайшего пути

Цель: научиться находить кратчайшие пути в графе при помощи алгоритма Дейкстры; получение навыком при решении задач нахождения пути в графе; закрепить навыки моделирования графов в графической среде Grafoanalizator1.3.3 rus, Простой граф, Grin.

Задачи:

1. Закрепить знания основных понятий теории графов.

2. Приобрести практические умения использования специального программного обеспечения для моделирования.

3. Использовать математический аппарат теории графов.

4. Применение алгоритмов поиска кратчайшего пути.

5. Планирование структуры сети с помощью графа с оптимальным расположением узлов.

Материальное обеспечение:

Программы для графического представления графов: Grafoanalizator1.3.3 rus, Простой граф, Grin, практическая работа.

Теоретическая часть:

Нахождение кратчайшего пути на сегодняшний день является жизненно необходимой задачей и используется практически везде, начиная от нахождения оптимального маршрута между двумя объектами на местности (например, кратчайший путь от дома до университета), в системах автопилота, для нахождения оптимального маршрута при перевозках, коммутации информационного пакета в сетях и т.п.

Кратчайший путь рассматривается при помощи некоторого математического объекта, называемого графом. Поиск кратчайшего пути ведется между двумя заданными вершинами в графе. Результатом является путь, то есть последовательность вершин и ребер, инцидентных двум соседним вершинам, и его длина.

Описываемый в данном разделе алгоритм позволяет находить в графе кратчайший путь между двумя выделенными вершинами и при положительных длинах дуг. Этот алгоритм предложенный в 1959 г. Дейкстрой, считается одним из наиболее эффективных алгоритмов решения задачи.

Главная идея, лежащая в основе алгоритма Дейкстры, предельно проста. Предположим, что нам известны вершин, ближайших к вершине (близость любой вершины x к вершине определяется длиной кратчайшего пути, ведущего из в 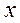). Пусть также известны сами кратчайшие пути, соединяющие вершину с выделенными m вершинами). Покажем теперь, как может быть определена -я ближайшая к вершина.

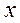Окрасим вершину и ближайших к ней вершин. Построим для каждой неокрашенной вершины пути, непосредственно соединяющие с помощью дуг каждую окрашенную вершину с . Выберем из этих путей кратчайший, и будем считать его условно кратчайшим путем из вершины в вершину .

Какая же из неокрашенных вершин является -й ближайшей к вершиной? Та, для которой условно кратчайший путь имеет наименьшую длину. Это обусловливается тем, что кратчайший путь из вершины в -ю ближайшую вершину при положительном значении длин всех дуг должен содержать в качестве промежуточных лишь окрашенные вершины, т. е. вершины, входящие в число вершин, ближайших к вершине .

Итак, если известны ближайших к вершин, то -я ближайшая к вершина может быть найдена так, как это описано выше. Начиная с , описанная процедура может повторяться до тех пор, пока не будет получен кратчайший путь, ведущий из вершины к вершине .

Алгоритм работает только для графов без рёбер отрицательного веса.

Любая задача,требующая нахождения оптимальных маршрутов может быть выполнена с помощью алгоритма Дейкстры. Это касается и сетей, и транспортных потоков, и обработка графов. Очень часто используется не сам алгоритм в чистом виде, а его модификация.

Примеры:

1. При эвакуации населения из очагов бедствия оптимальные маршруты до пунктов сбора транспорта для каждой группы людей(дом,улица,школа и т.д) в штабе МЧС рассчитывает программа на основе алгоритма Дейкстры.

2. Компьютерная игра. Указываете точку назначения для персонажа и он движется туда по кратчайшему маршруту. Это тоже алгоритм Дейкстры.

3. Дана сеть автомобильных дорог, соединяющих города Гомельской области. Некоторые дороги односторонние. Найти кратчайшие пути от города Гомеля до каждого города области (если двигаться можно только по дорогам).

4. Имеется некоторое количество авиарейсов между городами мира, для каждого известна стоимость. Стоимость перелёта из A в B может быть не равна стоимости перелёта из B в A. Найти маршрут минимальной стоимости (возможно, с пересадками) от Милана до Минска.

Алгоритм широко применяется в программировании и технологиях, например, его использует протокол OSPF для устранения кольцевых маршрутов.

OSPF разбивает процесс построения таблицы маршрутизации на 2 этапа.

Второй этап состоит в нахождении оптимальных маршрутов с помощью полученного графа. Задача нахождения оптимального пути на графе является достаточно сложной и ёмкой. В протоколе OSPF для её решения используется итеративный алгоритм Дейкстры. Каждый маршрутизатор считает себя центром сети и ищет оптимальный маршрут до каждой известной ему сети. В каждом найденном таким образом маршруте запоминается только один шаг - до следующего маршрутизатора, в соответствии с принципом одношаговой маршрутизации. Данные об этом шаге и попадают в таблицу маршрутизации. Если несколько маршрутов имеют одинаковую метрику до сети назначения, то в таблице маршрутизации запоминаются первые шаги всех этих маршрутов".

Алгоритм

1. Каждой вершине 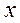в ходе алгоритма присваивается число , равное длине кратчайшего пути из вершины в вершину 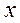и включающем только окрашенные вершины. Положить и для всех остальных вершин графа. Окрашиваем вершину и полагаем , где – последняя окрашенная вершина.

2. Для каждой неокрашенной вершины 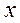пересчитывается величина по следующей формуле:

3. Если для всех неокрашенных вершин, то алгоритм заканчивается т. к. отсутствуют пути из вершины в неокрашенные вершины. Иначе окрашивается та вершина, для которой величина является минимальной. Окрашивается и дуга, ведущая в эту вершину в соответствии с выражением и полагаем .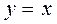

4. Если 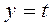, кратчайший путь из в найден. Иначе переходим к шагу 2.

Каждый раз окрашивается вершина и дуга, заходящая в эту вершину. Окрашенные дуги не могут образовывать цикл, а образуют в исходном графе дерево с корнем (началом) в вершине . Это дерево называют ориентированным деревом кратчайших путей. Путь из в принадлежит этому дереву. При поиске одного кратчайшего пути процедура наращивания завершается при достижении конечной вершины этого пути. Нам же необходимо получить все кратчайшие пути начинающиеся в вершине №1. Для этого процедуру наращивания ориентированного дерева продолжается до тех пор, пока все вершины не будут включены. Таким образом, мы получаем ориентированное дерево кратчайших путей, которое является покрывающим деревом графа.

Иногда в графе имеются несколько кратчайших путей. Кратчайший путь будет единственным, если в алгоритме ни разу не возникает неоднозначность при окрашивании дуги.

Отметим, что главным условием успешного применения алгоритма Дейкстры к задаче на графе является неотрицательность длин дуг этого графа

Для графа с отрицательными весами применяется более общий алгоритм — Алгоритм Дейкстры с потенциалами.

Пример выполнения задания.

Требуется найти кратчайшие расстояния от 1-й вершины до всех остальных для графа, представленного на рисунке:

№

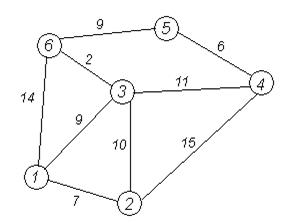
Алгоритм

Конкретные действия

Инициализация.

Cтартовая вершина, от которой строится дерево кратчайших путей - вершина № 1. Задаем стартовые условия: d(1)=0, d(x)=∞. Окрашиваем вершину № 1, y=1. Находим ближайшую вершину к окрашенной нами, используя формулу:

. Составим матрицу длин кратчайших дуг для данного графа.

№/№	1	2	3	4	5	6
1		7	9			14
2	7		10	15
3	9	10		11		2
4		15	11		6
5				6		9
6	14		2		9

или

Первый шаг. Рассмотрим шаг алгоритма Дейкстры.

d(2)=min{d(2) ; d(1)+a(1,2)}=min{∞; 0+7}=7 d(3)=min{d(3) ; d(1)+a(1,3)}=min{∞; 0+9}=9 d(4)=min{d(4) ; d(1)+a(1,4)}=min{∞; 0+∞}=∞ d(5)=min{d(5) ; d(1)+a(1,5)}=min{∞; 0+∞}=∞ d(6)=min{d(6) ; d(1)+a(1,6)}=min{∞; 0+14}=14 Минимальную длину имеет путь от вершины № 1 до вершины № 2 d(2)=7. Включаем вершину № 2 в текущее ориентированное дерево, а так же дугу ведущую в эту вершину. Согласно выражению это дуга (1,2).

Второй шаг.

d(3)=min{d(3) ; d(2)+a(2,3)}=min{9; 7+10}=9 d(4)=min{d(4) ; d(2)+a(2,4)}=min{∞; 7+15}=22 d(5)=min{d(5) ; d(2)+a(2,5)}=min{∞; 7+∞}=∞ d(6)=min{d(6) ; d(2)+a(2,6)}=min{14; 7+∞}=14 Минимальную длину имеет путь от вершины № 1 до вершины № 3 d(3)=9. Включаем вершину № 3 в текущее ориентированное дерево, а так же дугу ведущую в эту вершину. Согласно выражению это дуга (1,3)

Третий шаг.

d(4)=min{d(4) ; d(3)+a(3,4)}=min{22; 9+11}=20 d(5)=min{d(5) ; d(3)+a(3,5)}=min{∞; 9+∞}=∞ d(6)=min{d(6) ; d(3)+a(3,6)}=min{14; 9+2}=11 Минимальную длину имеет путь от вершины № 1 до вершины № 6 d(6)=11. Включаем вершину № 6 в текущее ориентированное дерево, а так же дугу ведущую в эту вершину. Согласно выражению это дуга (1,6)=(1,3)+(3,6)

Четвертый шаг.

d(4)=min{d(4) ; d(6)+a(6,4)}=min{20; 11+∞}=20 d(5)=min{d(5) ; d(6)+a(6,5)}=min{∞; 11+9}=20 Минимальную длину имеет путь от вершины № 1 до вершины № 4 и № 5 d(4)=d(6)=20. Включаем вершину № 4 и № 5 в текущее ориентированное дерево, а так же дугу ведущую в эту вершину. Согласно выражению это дуга (1,4)=(1,3)+(3,4) и (1,5)=(1,3)+(3,6)+(6,5).

Заключение.

Мы получили ориентированное дерево кратчайших путей начинающихся в вершине №1 для исходного графа. d(1)=1 Длина маршрута L=0 d(2)=1-2 Длина маршрута L=7 d(3)=1-3 Длина маршрута L=9 d(4)=1-3-4 Длина маршрута L=20 d(5)=1-3-6-5 Длина маршрута L=20 d(6)=1-3-6 Длина маршрута L=11

Пример выполнения задание № 2

Требуется найти кратчайшие расстояния от 1-й вершины до всех остальных для графа, представленного на рисунке:

Решение:

№

Алгоритм

Конкретные действия

Инициализация.

. Составим матрицу длин кратчайших дуг для данного графа.

№/№	1	2	3	4	5	6
1		10	18	8
2	10		16	9	21
3		16				15
4	7	9				12
5						23
6			15		23

или

Первый шаг. Рассмотрим шаг алгоритма Дейкстры.

d(2)=min{d(2) ; d(1)+a(1,2)}=min{∞; 0+10}=10 d(3)=min{d(3) ; d(1)+a(1,3)}=min{∞; 0+18}=18 d(4)=min{d(4) ; d(1)+a(1,4)}=min{∞; 0+8}=8 d(5)=min{d(5) ; d(1)+a(1,5)}=min{∞; 0+∞}=∞ d(6)=min{d(6) ; d(1)+a(1,6)}=min{∞; 0+∞}=∞ Минимальную длину имеет путь от вершины № 1 до вершины № 4 d(4)=8. Включаем вершину № 4 в текущее ориентированноe дерево, а так же дугу ведущую в эту вершину. Согласно выражению это дуга (1,4)

Второй шаг.

d(2)=min{d(2) ; d(4)+a(4,2)}=min{10; 8+9}=10 d(3)=min{d(3) ; d(4)+a(4,3)}=min{18; 8+∞}=18 d(5)=min{d(5) ; d(4)+a(4,5)}=min{∞; 8+∞}=∞ d(6)=min{d(6) ; d(4)+a(4,6)}=min{∞; 8+12}=20 Минимальную длину имеет путь от вершины № 1 до вершины № 2 d(2)=10. Включаем вершину № 2 в текущее ориентированноe дерево, а так же дугу ведущую в эту вершину. Согласно выражению это дуга (1,2)

Третий шаг.

d(3)=min{d(3) ; d(2)+a(2,3)}=min{18; 10+16}=18 d(5)=min{d(5) ; d(2)+a(2,5)}=min{∞; 10+21}=31 d(6)=min{d(6) ; d(2)+a(2,6)}=min{20; 10+∞}=20 Минимальную длину имеет путь от вершины № 1 до вершины № 3 d(3)=18. Включаем вершину № 3 в текущее ориентированноe дерево, а так же дугу ведущую в эту вершину. Согласно выражению это дуга (1,3)

Четвертый шаг.

d(5)=min{d(5) ; d(3)+a(3,5)}=min{31; 18+∞}=31 d(6)=min{d(6) ; d(3)+a(3,6)}=min{20; 18+15}=20 Минимальную длину имеет путь от вершины № 1 до вершины № 6 d(6)=20. Включаем вершину № 6 в текущее ориентированноe дерево, а так же дугу ведущую в эту вершину. Согласно выражению это дуга (4,6)

Пятый шаг.

d(5)=min{d(5) ; d(6)+a(6,5)}=min{31; 20+23}=31 Минимальную длину имеет путь от вершины № 1 до вершины № 5 d(5)=31. Включаем вершину № 5 в текущее ориентированноe дерево, а так же дугу ведущую в эту вершину. Согласно выражению это дуга (2,5)

Заключение.

Мы получили ориентированное дерево кратчайших путей начинающихся в вершине №1 для исходного графа. d(1)=1 Длина маршрута L=0 d(2)=1-2 Длина маршрута L=10 d(3)=1-3 Длина маршрута L=18 d(4)=1-4 Длина маршрута L=8 d(5)=1-2-5 Длина маршрута L=31 d(6)=1-4-6 Длина маршрута L=20 Ориентированное дерево с корнем в вершине №1:

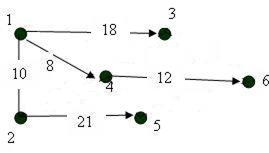
Задание.

1. Найти кратчайшие расстояния от 1-й вершины до всех остальных для графа, представленного на рисунке. Используя программное обеспечение, проверьте другие алгоритмы вычисления кратчайшего пути.