Пример № 1 выполнения задания 2
На заданной сети найти максимальный поток из X4 в X1 и минимальный разрез.
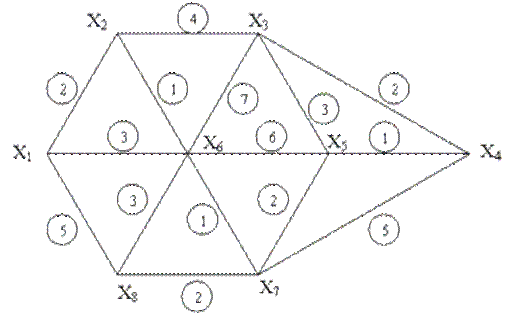
Решение
Необходимо заполнить таблицу:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| t X1 | 2, +Х2 | 1, +Х6 | 2, +Х8 | 1, +Х6 | 1, +Х6 | 1,+Х8 | |
| X2 | 2, +Х3 | 1, +Х3 | 1, +Х6 | ||||
| X3 | 2, +Х4 | 1, +Х5 | 2, +Х5 | 1, +Х5 | |||
| s X4 | ∞,+Х4 | ∞,+Х4 | ∞,+Х4 | ∞,+Х4 | ∞,+Х4 | ∞,+Х4 | ∞,+Х4 |
| X5 | 1, +Х4 | 1, +Х4 | 2, +Х7 | 2, +Х7 | 2, +Х7 | 1, +Х7 | |
| X6 | 2, Х3 | 1, +Х5 | 2, +Х7 | 1, +Х7 | 2, +Х5 | 1, Х5 | |
| X7 | 5, +Х4 | 5, +Х4 | 5, +Х4 | 3, +Х4 | 2, +Х4 | 1, +Х4 | |
| X8 | 2, +Х7 | 1, +Х6 | |||||
| V | 2 | 1 | 2 | 1 | 1 | 1 |

После первого шага увеличиваем потоки в дугах, которые сначала были везде = 0.
Далее продолжаем наращивать поток по цепям:
Х4, Х3, Х2, Х1, V1 = 2
Х4, Х5, Х6, Х1, V2 = 1
Х4, Х7, Х8, Х1, V3 = 2
Х4, Х7, Х6, Х1, V4 = 1
Х4, Х7, Х5, V5 = 1
Х4, Х7, Х5, Х6, Х8, V6 = 1
 , т.е. максимальный поток = 8.
, т.е. максимальный поток = 8.
На последнем, 7-ом шаге, на котором мы не достигли (не можем пометить) вершину t = Х1 находим все помеченные вершины:
Xs = {X4}
и непомеченные вершины
Xt = {X1, X2, X3, X5, X6, X7, X8}.
Минимальный разрез – ребра, один конец которых лежит в Xs, а другой в Xt.
В нашем случае это:
(Х4, Х3), V(Х4, Х3) = 2;
(Х4, Х5), V(Х4, Х5) = 1;
(Х4, Х7), V(Х4, Х7) = 5

Т.е. величина минимального разреза совпадает с максимальным потоком.
Пример № 2 выполнения задания № 2.
Постановка задачи поиска максимального потока: найти максимальный поток из  в
в 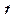 для транспортной сети (рисунок) с помощью алгоритма Форда – Фалкерсона:
для транспортной сети (рисунок) с помощью алгоритма Форда – Фалкерсона:
|
|
|

Решение:
| № | Алгоритм | Конкретные действия |
| 1. | 1-я итерация | 1.  .
2.1 (Второй шаг, первая итерация – подобное обозначение идет далее для всех шагов алгоритма). Производим помечивание вершин и дуг, результат показан на рисунке. Вершина 6 получила метку .
2.1 (Второй шаг, первая итерация – подобное обозначение идет далее для всех шагов алгоритма). Производим помечивание вершин и дуг, результат показан на рисунке. Вершина 6 получила метку  . .

|
| 2. | 2-я итерация | 3.1.  .
4.1. .
4.1.  ; ;
 ; ;
 .
2.2. Заново осуществляется помечивание. Вершина 6 снова получает метку .
2.2. Заново осуществляется помечивание. Вершина 6 снова получает метку 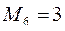 (смотри рисунок). (смотри рисунок).

|
| 3. | 3-я итерация | 3.2.  .
4.2. .
4.2. 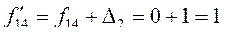 ; ;
 ; ;
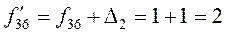 .
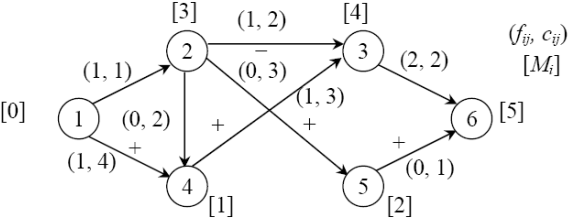
2.3. Осуществляется помечивание. При этом из вершины 3 прямых допустимых дуг не выходит, однако дуга 2–3 является допустимой в обратном направлении, и вершина 2 получает метку .
2.3. Осуществляется помечивание. При этом из вершины 3 прямых допустимых дуг не выходит, однако дуга 2–3 является допустимой в обратном направлении, и вершина 2 получает метку  . Вершина 6 получает метку . Вершина 6 получает метку  (смотри рисунок). (смотри рисунок).
|
| 4. | 4-я итерация | 3.3.  .
4.3. .
4.3. 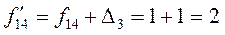 ; ;
 ; ;
 ; ;
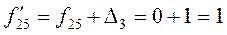 ; ;
 .
2.4. Осуществляется помечивание. При этом из вершины 3 допустимые дуги не выходят. Вершина 6 не получает метку (смотри рисунок). Переходим к шагу 5. .
2.4. Осуществляется помечивание. При этом из вершины 3 допустимые дуги не выходят. Вершина 6 не получает метку (смотри рисунок). Переходим к шагу 5.

|
| 5. | 5.  .
Минимальный разрез образуют насыщенные дуги 3–6 и 5–6. Пропускная способность минимального разреза .
Минимальный разрез образуют насыщенные дуги 3–6 и 5–6. Пропускная способность минимального разреза 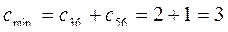 . Условия теоремы Форда – Фалкерсона выполняются . Условия теоремы Форда – Фалкерсона выполняются   задача решена правильно.
Алгоритм Форда – Фалкерсона используется при решении многих практических задач. Одна из них – задача об источниках и потребителях. задача решена правильно.
Алгоритм Форда – Фалкерсона используется при решении многих практических задач. Одна из них – задача об источниках и потребителях.
|
Задание:
|
|
|
1.С помощью матрицы смежности найти компоненты сильной связности ориентированного графа D. При решении использовать программу Grafoanalizator1.3.3 rus, Простой граф

| 
| 
|
| Вариант1 | Вариант 2 | Вариант 3 |
2. Дана сеть:

Определить максимальный поток в сети при начальных значениях дуговых потоков:  ,
, 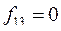 ,
, 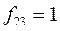 ,
,  ,
,  ,
,  ,
,  .
.
Варианты значений пропускных способностей дуг для задания:
 Порядок выполнения работы:
Порядок выполнения работы:
1. Изучить примеры выполнения заданий 1 и 2 .
2. Выполнить задание.
3. Оформить отчет.
Содержание отчета:
1. Тема.
2. Цель.
3. Задачи.
4. Материальное обеспечение.
5. Практическое задание.
Вопросы для самоконтроля:
1. Перечислите основные компоненты связности графов.
2. В чем смысл матрицы достижимости?
3. Запишите теорему Форда-Фалкерсона 1 (о максимальном потоке и минимальном разрезе).
Практическая работа № 10
Тема: Решение задач по теории графов. Нахождение путей в графе
Цель: реализовать алгоритмы обработки графовых структур: поиск различных путей; получение навыком при решении задач нахождения пути в графе; закрепить навыки моделирования графов в графической среде Grafoanalizator1.3.3 rus, Простой граф, Grin.
|
|
|
Задачи:
1. Закрепить знания основных понятий теории графов.
2. Приобрести практические умения использования специального программного обеспечения для моделирования.
3. Использовать математический аппарат теории графов.
4. Применение алгоритмов поиска кратчайшего пути.
5. Планирование структуры сети с помощью графа с оптимальным расположением узлов.
Материальное обеспечение:
Программы для графического представления графов: Grafoanalizator1.3.3 rus? Простой граф, Grin.
практическая работа. Интернет ссылка: http://inf.reshuege.ru/test?theme=203
Теоретическая часть:
В основе построения большинства алгоритмов на графах лежит систематический перебор вершин графа, при котором каждая вершина просматривается в точности один раз, а количество просмотров ребер графа ограничено заданной константой (лучше – не более одного раза).
Один из основных методов проектирования графовых алгоритмов – это поиск (или обход графа) в глубину (depth first search, DFS), при котором начиная с произвольной вершины v0, ищется ближайшая смежная вершина v, для которой в свою очередь осуществляется поиск в глубину (т.е. снова ищется ближайшая, смежная с ней вершина) до тех пор, пока не встретится ранее просмотренная вершина, или не закончится список смежности вершины v (то есть вершина полностью обработана). Если нет новых вершин, смежных с v, то вершина v считается использованной, идет возврат в вершину, из которой попали в вершину v, и процесс продолжается до тех пор, пока не получим v = v0. Иными словами, поиск в глубину из вершины v основан на поиске в глубину из всех новых вершин, смежных с вершиной v.
|
|
|
Путь, полученный методом поиска в глубину, в общем случае не является кратчайшим путем из вершины v в вершину u. Это общий недостаток поиска в глубину. На рисунке показан путь, полученный обходом графа в глубину.


Указанного недостатка лишен другой метод обхода графа – поиск в ширину (breadth first search, BFS). Обработка вершины v осуществляется путем просмотра сразу всех новых соседей этой вершины. При этом полученный путь является кратчайшим путем из одной вершины в другую.
показан путь, найденных методом поиска в ширину
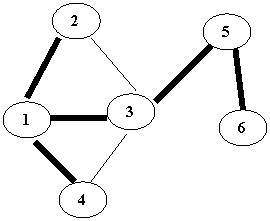

При использовании алгоритмов DFS и BFS графы обходят разными способами, получая при этом некоторые подграфы, которые имеют специфические названия: каркасы, остовы или стягивающие деревья. Все вершины исходного графа входят в полученное стягивающее дерево, а все ветви дерева – это множество ребер из все множеств ребер графа.
Произвольный путь в графе, проходящий через каждое ребро графа точно один раз, называется эйлеровым путем. При этом, если по некоторым вершинам путь проходит неоднократно, то он является непростым. Если путь замкнут, то имеем эйлеров цикл. Для существования эйлерова пути в связном графе необходимо и достаточно, чтобы граф содержал не более двух вершин нечетной степени.
Путь в графе, проходящий в точности один раз через каждую вершину графа (а не каждое ребро) и соответствующий цикл называются гамильтоновыми и существуют не для каждого графа, как и эйлеров путь. В отличие от эйлеровых путей неизвестно ни одного простого необходимого и достаточного условия для существования гамильтоновых путей. Неизвестен даже алгоритм полиномиальной сложности, проверяющий существование гамильтонова пути в произвольном графе. Проблема существования гамильтонова пути принадлежит к классу так называемых NP-полных задач.
В теории алгоритмов классом NP (от англ. non-deterministic polynomial) называют множество задач распознавания (англ.), решение которых при наличии некоторых дополнительных сведений (так называемого сертификата решения) можно «быстро» (за время, не превосходящее полинома от размера данных) проверить на машине Тьюринга.
NP-полная задача — задача из класса NP, к которой можно свести любую другую задачу из класса NP за полиномиальное время. Таким образом, NP-полные задачи образуют в некотором смысле подмножество «самых сложных» задач в классе NP; и если для какой-то из них будет найден «быстрый» алгоритм решения, то и любая другая задача из класса NP может быть решена так же «быстро».
При решении некоторых практических задач возникает необходимость поиска максимального пути ( пути с наибольшей суммой длин дуг). Такая задача сводится к задаче нахождения минимального пути заменой знаков при длинах дуг ( в матрице весов C) на противоположные . При этом необходимым является требование отсутствия в ориентированном графе контуров положительной длины .
Поиск путей
знать:
o если в город R можно приехать только из городов X, Y, и Z, то число различных путей из города A в город R равно сумме числа различных путей проезда из A в X, из A в Y и из A в Z, то есть NR = NX + NY + NZ, где NQ обозначает число путей из вершины A в некоторую вершину Q
o число путей конечно, если в графе нет циклов – замкнутых путей
Пример задания:
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?


Решение (1 вариант, подстановки):
1) начнем считать количество путей с конца маршрута – с города К
2) будем обозначать через NX количество различных путей из города А в город X
3) общее число путей обозначим через N
4) по схеме видно, что NБ = NГ = 1
5) очевидно, что если в город X можно приехать только из Y, Z, то NX = NY + NZ, то есть нужно сложить число путей, ведущих из A во все города, откуда можно приехать в город X
6) поскольку в K можно приехать из Е, Д, Ж или И, поэтому
N = NК = NД + NЕ + NЖ + NИ
7) в город И можно приехать только из Д, поэтому NИ = NД
8) в город Ж можно приехать только из Е и В, поэтому
NЖ = NЕ + NВ
9) подставляем результаты пп. 6 и 7 в формулу п. 5:
N = NВ + 2NЕ + 2NД
10) в город Д можно приехать только из Б и В, поэтому
NД = NБ + NВ
так что
N = 2NБ + 3NВ + 2NЕ
11) в город Е можно приехать только из Г, поэтому NЕ = NГ так что
N = 2NБ + 3NВ + 2NГ
12) по схеме видно, что NБ = NГ = 1, кроме того, NВ = 1 + NБ + NГ = 3
13) окончательно N = 2NБ + 3NВ + 2NГ = 2·1 + 3·3 + 2·1 = 13
14) Ответ: 13.
Решение (2 вариант, удобная форма записи):
1) начнем считать количество путей с конца маршрута – с города К
2) записываем для каждой вершины, из каких вершин можно в нее попасть

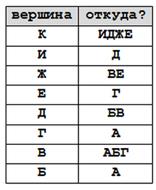
К ← ИДЖЕ
И ← Д
Ж ← ВЕ
Е ← Г
Д ← БВ
Г ← А
В ← АБГ
Б ← А
3) теперь для удобства «обратного хода» вершины можно отсортировать так[1], чтобы сначала шли все вершины, в которые можно доехать только из начальной точки А:

Б ← А
Г ← А
затем на каждом шаге добавляем те вершины, в которые можно доехать из уже добавленных в список (и из исходной точки):
В ← АБГ
Е ← Г
далее добавляем все вершины, куда можно доехать из А, Б, Г, В и Е:
Д ← БВ
Ж ← ВЕ
на следующем шаге добавляем вершину И
И ←Д
и, наконец, конечную. вершину
К ←ИДЖЕ
именно в таком порядке мы и будем вычислять количество путей для каждой вершины
[1] Такая процедура называется топологической сортировкой графа.
4) теперь идем по полученному списку вершин, полагая, что количество вариантов попасть в вершину равно суммарному количеству вариантов попасть в ее непосредственных предшественников.
NБ = 1, NГ = 1
NВ = 1+1+1 = 3, NЕ = 1
NД = 1+3 = 4, NЖ = 3 + 1 = 4
NИ = 4,
N = NК = 4 + 4 + 4 + 1 = 13
5) заметим, что вершины можно и не сортировать специально, а просто выбирать возможный порядок вычисления: проверять, какие значения известны и какие можно рассчитать с их помощью на следующем шаге
6) Ответ: 13.
Возможные ловушки и проблемы:
o очень важна аккуратность и последовательность; сначала идем от конечной точки к начальной, выписывая все вершины, из которых можно приехать в данную; затем идем обратно, определяя числовые значения
o построение полного дерева маршрутов – занятие трудоемкое и достаточно бесперспективное, даже грамотные учителя информатики здесь в большинстве случаев что-то забывают и ошибаются
Решение (3 вариант, перебор вершин по алфавиту):
1) Запишем вершины в алфавитном порядке и для каждой из них определим, из каких вершин можно в нее попасть


Б ← А
В ← АБГ
Г← А
Д ←БВ
Е ← Г
Ж ← ВЕ
И ← Д
К ← ИДЖЕ
2) теперь определяем количество путей; сначала ставим 1 для тех вершин, в которые можно проехать только из начальной (А):

3) затем на каждом шаге добавляем те вершины, в которые можно доехать из уже добавленных в список (и из исходной точки):

4) следующий шаг

5) и последние 2 шага
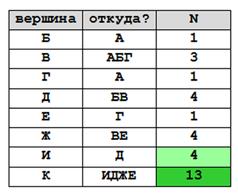
6) Ответ: 13.
Решение (4 вариант, перебор всех путей с начала, А. Яфарова):
1) запишем все вершины, в которые есть прямой путь из вершины A: Б, В и Г; получается три начальных отрезка:
АБ, АВ, АГ
2) рассмотрим маршрут АБ: из Б можно ехать в В и Д, поэтому получаем два маршрута:
АБВ, АБД
3) рассматриваем конечные точки этих маршрутов: из В можно ехать в Д и Ж, а из Д – в И и К:
АБВД, АБВЖ, АБДИ, АБДК
4) снова смотрим на конечные точки: из Д едем в И и К, из Ж и И – только в К:
АБВДИ, АБВДК, АБВЖК, АБДИК, АБДК
5) из И едем только в К, таким образом, все возможные маршруты, содержащие участок АБ, доведены до конечной точки К, всего 5 таких маршрутов:
АБВДИК, АБВДК, АБВЖК, АБДИК, АБДК
6) затем аналогично рассматриваем маршруты, которые начинаются с АВ:
АВД, АВЖ
АВДИ, АВДК, АВЖК
АВДИК, АВДК, АВЖК
всего 3 маршрута
7) наконец, остается рассмотреть маршруты, которые начинаются с АГ:
АГВ, АГЕ
АГВД, АГВЖ, АГЕЖ, АГЕК
АГВДИ, АГВДК, АГВЖК, АГЕЖК, АГЕК
АГВДИК, АГВДК, АГВЖК, АГЕЖК, АГЕК
всего 5 маршрутов
8) складываем количество маршрутов для всех начальных участков: 5 + 3 + 5 = 13
9) Ответ: 13.
Возможные проблемы:
o при большом количестве маршрутов легко запутаться и что-то пропустить
o Решение (5 вариант, графический):
o 1) Главную идею решения: (число дорог в город N есть сумма дорог, приводящих в города, из которых есть прямой проезд в город N), отразим на самой схеме, показывая на ней ЧИСЛО ДОРОГ, приводящих в каждый город.
o 2) Последовательность очевидна: начинаем с Б и Г (городов, куда есть по 1-й дороге из А)
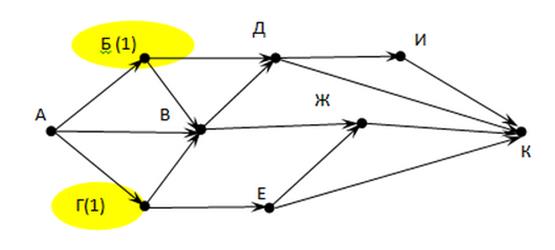
3) Посчитаем дороги в В: 1 (из A)+ 1(дороги города Б)+ 1(дороги города В)= 3
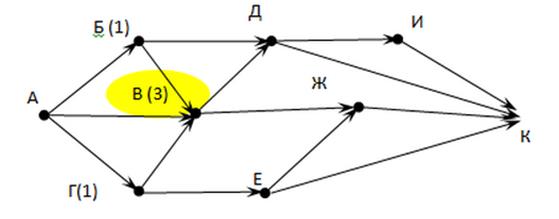
4) Аналогично посчитаем дороги в Д, И, Е, Ж:

5) Определяем число дорог в город К, как сумму дорог в города, с которыми он связан: Д, И, Ж, Е.
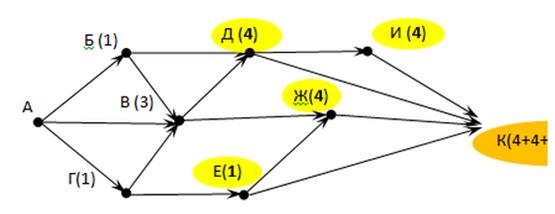
6) Ответ: 13.
Задания:
Выполнить задание и проверить с помощью программы Grin, Простой граф.
1. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?(ответ 12)

2. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж? (ответ 24)

3. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж? (Ответ 33) 
4. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? (Ответ: 23)

5.На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? (ответ: 17)

6.На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? (Ответ: 13)

7.На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж? (Ответ: 20)

8.На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? (Ответ: 12)
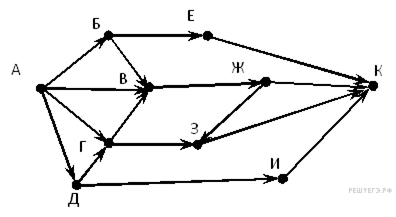
9.На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж? (Ответ:24)

10.На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? (Ответ: 17)
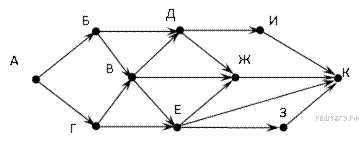
11. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж? (Ответ: 46)

12.На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город З? (Ответ 14)

13. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? (ответ: 16)

14. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? (Ответ: 14)

15. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город З? (Ответ: 8)

16.На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж? (Ответ:14)
17.На рисунке – схема дорог, связывающих города A, B, C, D, E, F, G H. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города A в город H? (Ответ: 14)

18.На рисунке – схема дорог, связывающих города A, B, C, D, E, F, G, H, K, L, M. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города A в город M? (Ответ:12)

19. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? (Ответ:23)

20. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город M?(Ответ:16)

21. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? (ответ:13)

22. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город И? (ответ:16)

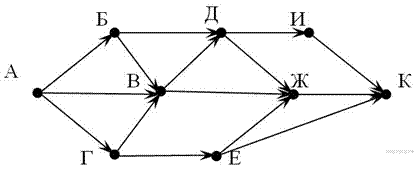
23. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? (ответ:13)

24. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город И? (ответ:16)

25. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город И? (Ответ: 11)

26. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город З? (Ответ: 9)

27. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Е? (Ответ:7 )

28. На рисунке – схема дорог, связывающих города A, B, C, D, E, F, G, H, K, L, M. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города A в город E? (ответ:4)

29. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город З? (ответ:3 )

30. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? (Ответ: 17)

Порядок выполнения работы:
1. Изучить примеры выполнения заданий.
2. Выполнить задание.
3. Оформить отчет.
Содержание отчета:
1. Тема.
2. Цель.
3. Задачи.
4. Материальное обеспечение.
5. Практическое задание.
Вопросы для самоконтроля:
1. В поиск в графе иначе называется?
2. Что означает DFS и BFS?
3. Дайте определение NP-полная задача?
Практическая работа № 11
Тема : Решение задач по теории графов. Нахождение минимально доминирующих множеств (МДМ). Нахождение максимально независимых множеств (МНМ)
Цель: реализовать алгоритмы нахождения МДМ и МНМ; закрепить навыки моделирования графов в графической среде Grafoanalizator1.3.3 rus, Простой граф
Задачи:
1. Закрепить знания основных понятий теории графов.
2. Приобрести практические умения использования специального программного обеспечения для моделирования.
3. Использовать математический аппарат теории графов.
4. Планирование структуры сети с помощью графа с оптимальным расположением узлов.
Материальное обеспечение:
Программы для графического представления графов: Grafoanalizator1.3.3 rus, Простой граф, практическая работа.
Теоретическая часть:
Подмножество вершин S графа G = ( V , U ) называется доминирующим (внешне устойчивым), если каждая вершина из V — S смежна с некоторой вершиной из S . Другими словами, каждая вершина графа находится на расстоянии не более единицы от доминирующего множества. Доминирующее множество называется минимальным, нет другого доминирующего множества, содержащегося в нем. Минимальных доминирующих множеств в графе может быть несколько, и они не обязательно содержат одинаковое количество вершин. Минимальное доминирующее множество, имеющее наименьшую мощность называется наименьшим.
|
Подмножество вершин графа, являющееся одновременно независимым и доминирующим, называется ядром графа.
Понятие доминирующего множества переносится и на случай ориентированных графов. Подмножество S вершин орграфа называется доминирующим, если для любой вершины  существует такая вершина
существует такая вершина  , что
, что  где А - множество дуг орграфа Подмножество вершин S, являющееся одновременно и независимым, и доминирующим называется ядром орграфа.
где А - множество дуг орграфа Подмножество вершин S, являющееся одновременно и независимым, и доминирующим называется ядром орграфа.
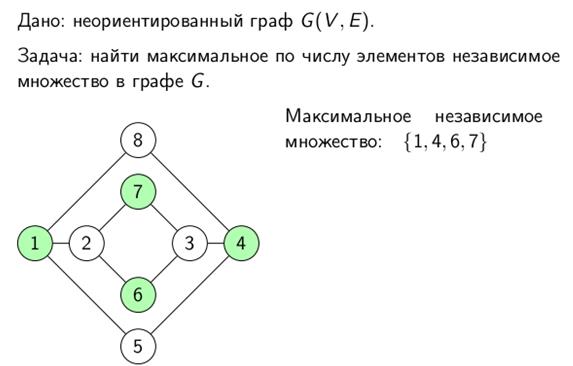
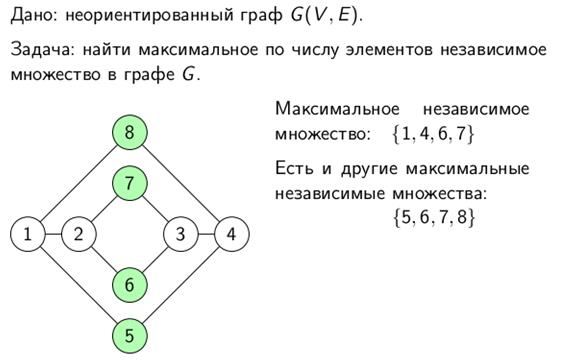
Множество вершин графа называется независимым, если никакие две вершины этого множества не соединены ребром. Другими словами, индуцированный этим множеством подграф состоит из изолированных вершин. Иногда также говорят, что каждое ребро графа инцидентно не более чем одной вершине из независимого множества. Задача разрешения выглядит так: существует ли в заданном графе G независимое множество размера k? Соответствующая ей оптимизационная задача, она же задача о независимом множестве, формулируется следующим образом: в заданном графе G требуется найти независимое множество максимального размера.
Иногда эту задачу называют поиском независимого множества максимального размера или максимального (по размеру) независимого множества. Не стоит путать это понятие с максимальным (по включению) независимым множеством, которое определяется как такое независимое множество вершин, что при добавлении к нему еще одной (любой) вершины исходного графа оно перестает быть независимым. Понятно, что таких множеств, вообще говоря, может быть несколько и разных размеров. Максимальное по включению независимое множество отнюдь не всегда является максимальным по размеру. В то же время, каждое независимое множество максимального размера по определению является также и максимальным по включению. Для нахождения (какого-то) максимального по включению независимого множества можно воспользоваться жадным алгоритмом, работающим за полиномиальное время, тогда как задача о независимом множестве максимального размера принадлежит к классу NP-полных задач.
Например, для графа G, изображенного на рисунке, a(G)=4, множества вершин {1,2,3,7}, {1,2,3,8}, {2,3,5,7}, {2,3,5,8} являются наибольшими независимыми, а {4,7} – максимальное независимое множество, не являющееся наибольшим.


 2
2





 1 3 7
1 3 7
 |  |  |



 5 4 6
5 4 6
8


Дата добавления: 2019-02-22; просмотров: 2383; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

