Максимальный поток и минимальный разрез
Теорема Форда-Фалкерсона 1 (о максимальном потоке и минимальном разрезе).
В любой сети существует максимальный поток. Величина максимального потока равна пропускной способности минимального разреза.
Теорема Форда-Фалкерсона 2.
Поток, вычисленный с помощью алгоритма Форда-Фалкерсона имеет максимальную величину, а разрез 
, где 
-множество вершин, помеченных при последнем помечивании, имеет минимальную пропускную способность.
Нахождение максимального потока и построение минимального разреза в сети с использованием алгоритма Форда-Фалкерсона
В данной задаче основным параметром на дугах сети является 
– пропускная способность. Пропускная способность показывает, сколько единиц потока может быть передано по дугам сети. Таким образом, потоком в сетиD = [N, M] называется неотрицательная вещественная функция, удовлетворяющая условиям:
1. ограниченности: поток по любой дуге сети не превосходит пропускной способности этой дуги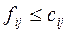 
;
2. сохранения: суммарный поток, заходящий в любую вершину сети (кроме истока и стока), равен суммарному потоку, выходящему из этой вершины.
Дуга сети называется насыщенной, если поток по этой дуге равен пропускной способности этой дуги, т. е. 
.
Разрезом сетиназывается множество дуг, удаление которых из сети приводит к тому, что исток и сток оказываются несвязанными.
Пропускной способностью разрезаназывается число, равное сумме пропускных способностей дуг этого разреза. Разрез называется минимальным, если имеет наименьшую пропускную способность.
|
|
|
Отыскание минимального разреза – одна из основных задач анализа транспортных сетей. В силу конечности графа минимальный разрез может быть найден перебором всех разрезов, но этот путь, конечно, неприемлем для достаточно больших графов.
Минимальный разрез можно отыскать при помощи теоремы Форда – Фалкерсона: в любой транспортной сети величина любого максимального потокаравна пропускной способности любого минимального разреза.
Для нахождения максимального потока в сети разработан алгоритм Форда – Фалкерсона. Перед началом выполнения алгоритма все вершины сети нумеруются произвольным образом, кроме источника и стока (источник получает минимальный номер 1, сток – максимальный 
, где – число узлов).
Алгоритм состоит из следующих основных шагов:
1. Определить начальный поток в сети, сложив потоки по дугам, выходящим из источника.
2. Вершинам сети присвоить целочисленные метки, а дугам – знаки «+» и «–» по следующим правилам:
а) вершине-истоку присвоить метку 
;
б) находим непомеченнуювершину 
, смежную помеченнойвершине 
. Если поток по соединяющей вершины 
дуге меньше пропускной способности этой дуги, то происходит помечивание, иначе переходим к рассмотрению следующей вершины. Если вершина является образомпомеченной вершины , то происходит прямое помечивание (дуга в прямом направлении допустима): вершина получает метку, равную номеру вершины , соединяющая вершины дуга получает метку «+», переходим к рассмотрению следующей вершины. Если вершина не имеет ни одного помеченного прообраза, поток по дуге в прямом направлении больше 0, то происходит обратное помечивание (дуга допустима в обратном направлении): вершина получает метку, равную номеру вершины (являющейся в данном случае ее образом), соединяющая вершины 
дуга получает метку «–», происходит переход к рассмотрению следующей вершины. Процесс помечивания продолжается до тех пор, пока все удовлетворяющие этим условиям вершины не получат метку.
|
|
|
3. Если в результате процедуры помечивания вершина-сток метки не получила, то текущий поток – максимальный, переход к шагу 5. В противном случае перейти к пункту 4.
4. Рассмотреть последовательность вершин L, метка каждой из которых равна номеру следующей за ней вершины, и множество дуг МL, соединяющих соседние вершины из L.
|
|
|
Построение нового потока по схеме:
а) Если дуга принадлежит множеству МL (смотри выше) и имеет знак «+», то новый поток по этой дуге = старый поток по этой дуге + Δ (схему нахождения смотри далее).
б) Если дуга принадлежит множеству МL и имеет знак «–», то новый поток по этой дуге = старый поток по этой дуге – Δ.
в) Если дуга не принадлежит множеству МL, то поток по дуге оставляем без изменения.
Схема нахождения Δ:
I. 
, где для нахождения 
рассматриваются все дуги, принадлежащие множеству МL и имеющие знак «+», и для каждой такой дуги вычисляется разность между пропускной способностью дуги и потоком по этой дуге ( 
). Затем из этих значений разностей выбирается минимальное значение и присваивается .
II. Для нахождения 
рассматриваются все дуги, принадлежащие множеству МL и имеющие знак «–». Затем из этих дуг выбирается дуга с минимальным потоком ( 
), и значение потока по этой дуге присваивается .
Перейти к шагу 2.
5. Определяем максимальный поток, складывая начальный поток и все полученные изменения потока.
В оптимальном решении, т. е. когда найден максимальный поток, минимальный разрез образуется насыщенными дугами.
Дата добавления: 2019-02-22; просмотров: 6452; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!