Алгоритма проверки существования эйлерова пути

⇐ ПредыдущаяСтр 3 из 9Следующая ⇒

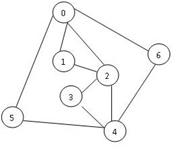
Представим динамику выполнения алгоритма проверки существования эйлерова пути (цикла) из вершины 0 для представленного на рисунке 1 графа.
Цикл существует.
Рисунок 1

Например, один из возможных путей прохождения всех ребер графа из вершины 0 может быть следующим:
0 – 1 – 2 – 0 – 6 – 4 – 2 – 3 – 4 – 5 – 0
В приведенном списке вершин, следующих за 0, каждая вершина является одновременно концом предыдущего ребра и началом следующего.
В соответствии с алгоритмом:
0 – степень 4;
1 – 2;
2 – 4;
3 – 2;
4 – 4;
5 – 2;
6 – 2;
Степени всех вершин четные, следовательно, эйлеров цикл в данном графе существует.

Рисунок 2

Граф, изображенный на рисунке 2 отличается от рисунка 1 только добавлением ребра (3 – 5).
При этом степени вершин 3 и 5 стали нечетными.
Согласно алгоритму проверки существования эйлерова цикла, основывающемуся на проверке четности степени каждой вершины, в данном графе цикла быть не может.
Однако, если учесть следствие, по которому в точности две вершины имеют нечетную степень, то и в графе, изображенном на рисунке 1 должен существовать эйлеров путь.
Пример такого пути: 3 – 2 – 4- 3 – 5 – 4 – 6 – 0 – 2 – 1 – 0 – 5.
При этом две вершины, имеющие нечетную степень, находятся на концах такого пути.

Алгоритма поиска гамильтонова пути

Представим динамику выполнения рекурсивного алгоритма поиска гамильтонова пути (цикла) из вершины 0 для графа, представленного на рисунке 3.

Рисунке 3.
Цикла не существует.
0-1
1-2
2-3
3-4
4-5
4-6
2-4
4-3
4-5
4-6
0-2
2-1
2-3
3-4
4-5
4-6
2-4
4-3
4-5
4-6
0-5
5-4
4-2
2-1
2-3
4-3
3-2
2-1
4-6
0-6
6-4
4-2
2-1
4-3
3-2
2-1
4-5
Представим динамику выполнения рекурсивного алгоритма поиска гамильтонова пути для представленного на рисунке 4 графа.

Цикл существует, например: 0 – 6 – 4 – 2 – 1 – 3 – 5 – 0.
Рисунке 4.
Продемонстрируем поиск цикла от вершины 1.
1-0
0-5
5-3
3-2
2-4
4-6
3-4
4-2
4-6
5-4
4-2
2-3
4-6
0-6
6-4
4-2
2-3
3-5
4-3
3-2
3-5
4-5
5-3
3-2
2-1

Искомый путь 1 – 0 – 6 – 4 – 5- 3 – 2 – 1 .

Инструкция к практической работе

1. Существует ли эйлеров цикл в графе G. Если существует, найдите его.

Решение:

А) Так как каждая вершина имеет чётную степень, то по критерию в этом графе существует эйлеров цикл: 1,4,6,9,10,8,5,3,2,4,7,10,11,8,6,5,2,1

Б) В этом графе также каждая вершина имеет чётную степень, значит, существует и эйлеров цикл: 1,2,3,4,5,3,1,4,5,2,1

В) Здесь каждая вершина имеет степень 5, то есть нечётную, следовательно, в этом графе (по критерию) нет эйлерова цикла.

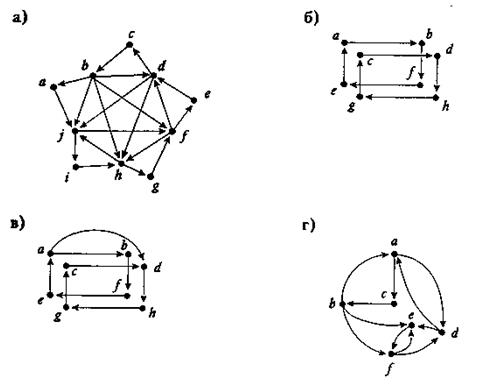
2. Какие из следующих ориентированных графов имеют эйлеровы циклы?

Решение:

а) Граф связный, найдём степени входа и выхода вершин (по теореме 5 степени входа и выхода каждой вершины должны совпадать):

indeg(a)=2, outdeg(a)=1, то есть нашлась вершина, у которой не совпадают степени входа и выхода, значит, граф не имеет эйлерова цикла.

б) Граф связный, найдём степени вершин:

indeg(a)=2 outdeg(a)=2

indeg(b)=2 outdeg(b)=2

indeg(c)=2 outdeg(c)=2

indeg(d)=2 outdeg(d)=2

indeg(e)=2 outdeg(e)=2

Следовательно, по теореме 5, граф имеет эйлеров цикл.

в) Граф связный, найдём степени вершин:

indeg(a)=2 outdeg(a)=2

indeg(b)=1 outdeg(b)=1

indeg(c)=3 outdeg(c)=1

Условия теоремы 5 не выполняются, значит, граф не имеет эйлерова цикла.

г) Граф связный, найдём степени вершин:

indeg(a)=2 outdeg(a)=1

Следовательно, т.к. условия теоремы 5 не выполняются то, граф не имеет эйлерова цикла.

2. Задача.Найдите эйлеров цикл в эйлеровом графе

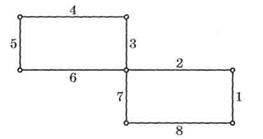
Решение. После выбора вершины а и прохождении рёбер 1 и 2 имеются три возможности выбора: рёбра 3, 6 или 7. Выбираем ребро 3 или 6. Например, ребро 3. Далее обходим оставшиеся рёбра и получаем эйлеров цикл 1, 2, 3, 4, 5, 6, 7, 8.

3.Задача. Найдите цикл, содержащий все вершины додекаэдра, причём в точности по одному разу каждую.

Решение.

Этот цикл: 1, 2, 3, 4, 5, 6, 19, 18, 14, 15, 16, 17, 7, 8, 9, 10, 11, 12, 13, 20.

Этот цикл называется гамильтоновым циклом.

Задание:

1. Проработать алгоритм выполнения поиска эйлерова и гамильтонова пути (изобразите графы, содержащие эти пути)

2. Среди приведённых ниже графов найдите те, которые имеют эйлеров и гамильтонов цикл. Результат проверить при помощи программы Grafoanalizator1.3.3.

2. Какие из следующих ориентированных графов имеют эйлеровы и гамильтоновы циклы? Результат проверить при помощи программы Grafoanalizator1.3.3.

Порядок выполнения работы:

1. Изучить инструкцию к практической работе.

2. Выполнить задание.

3. Оформить отчет.

Содержание отчета:

1. Тема.

2. Цель.

3. Задачи.

4. Материальное обеспечение.

5. Практическое задание.

Вопросы для самоконтроля:

1.Дайте определение эйлерова графа.

2.Сформулируйте алгоритм построения эйлерова цикла.

3.Какой граф называют гамильтоновым?

4.Существует ли эйлеров граф, обладающий висячей вершиной?

5.Чем отличается эйлеров путь от гамильтонова?

Практическая работа № 4

Тема:Решение задач по теории графов. Конечные графы. Бесконечные графы.

Цель: изучить теоретические основы конечных и бесконечных графов.

Задачи:

1.Закрепить знания основных понятий теории конечных и бесконечных графов.

2. Использовать математический аппарат теории графов

Материальное обеспечение:

практическое задание.

Теоретическая часть:

Конечный граф

Граф называется конечным, если число вершин и ребер в нем конечно, в противном случае – бесконечным.

Рассмотрим неориентированный граф G. Число ребер ρ ( v ), инцидентных вершине v, назовем локальной степенью графа в вершине v.

Если все числа ρ ( v ) для " v Î V, то граф называется локально-конечным.

Обозначим ρ ( v , u ) = ρ ( u , v ) – это число ребер, соединяющих вершины v и u, т.е. это кратность ребра ( v , u ). Тогда

Обозначим m ( G ) – число ребер в графе G. Т.к. каждое ребро будет учитываться в двух локальных степенях v и u, то запишем:

(1)

Теорема. Число вершин нечетной локальной степени в графе четно.

Доказательство. Воспользуемся формулой (1), т.е. сумма всех локальных степеней четна. Тогда, удалив из суммы все четные слагаемые, получим четное число, представляющее собой сумму нечетных степеней. Теорема доказана.

Граф называется однородным в степени k, если локальные степени всех вершин равны k. Примерами однородных графов являются правильные треугольники, многоугольники, многогранники.

Для однородных графов можно записать:

где n – число вершин графа G.

Для куба:

Пусть G – ориентированный граф. Тогда введем следующие обозначения:

¾ od ( v ) – число дуг, выходящих из вершины;

¾ id ( v ) – число дуг, заходящих в вершину.

Это локальные степени графа.

Петли, если они есть, считаются по одному разу и в od ( v ), и в id ( v ).

Аналогично считаются две кратности. Обозначим как ρ _o ( v , u ), ρ _i ( v , u ) число дуг, выходящих из v в u и из u в v соответственно.

Ориентированный граф называется однородным, если для " v Î V выполняется следующее: od ( v ) = id ( v ) = k.

Бесконечный граф

Примеры бесконечных однородных графов.

Бесконечные однородные графы находят широкое применение в задачах трассировки печатных соединений, т.к. их использование позволяет разбивать коммутационное поле печатных плат на элементарные ячейки одинаковой формы.

Бесконечным графом называется пара , , где 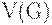— бесконечное множество элементов, называемое вершинами, а — бесконечное семейство неупорядоченных пар элементов из 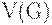, называемых ребрами.

Если оба множества 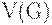и — счетны, то называется счетным графом. Заметим, что наши определения исключают те случаи, когда 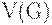— бесконечно, а — конечно. Такие объекты являются всего лишь конечными графами с бесконечным множеством изолированных вершин. Когда — бесконечно, а 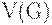— конечно, такие объекты являются конечными графами с бесконечным числом петель или кратных ребер.

Некоторые определения таких понятий, как "смежный", "инцидентный", "изоморфный", "подграф", "объединение", "связный", "компонента" переносятся на бесконечные графы.

Степенью вершины 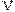бесконечного графа называется мощность множества ребер, инцидентных 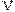Степень вершины может быть конечной или бесконечной. Бесконечный граф, все вершины которого имеют конечные степени, называется локально конечным. Хорошо известным примером такого графа является бесконечная квадратная решетка, часть которой изображена на рисунке. Локально счетный бесконечный граф — это граф, все вершины которого имеют счетную степень. Под счетным множеством здесь и в дальнейшем понимается бесконечное множество, допускающее взаимно однозначное отображение на множество натуральных чисел.

Теорема Каждый связный локально счетный бесконечный граф является счетным.

Доказательство

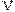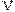Пусть — произвольная вершина такого бесконечного графа, и пусть — множество вершин, смежных , — множество всех вершин, смежных вершинам из , и т.д. По условию теоремы — счетно и, следовательно, множества тоже счетны. Здесь используется тот факт, что объединение не более чем счетного множества счетных множеств счетно. Следовательно, — последовательность множеств, объединение которых счетно. Кроме того, эта последовательность содержит каждую вершину бесконечного графа в силу его связности. Отсюда и следует нужный результат.

Следствие Каждый связный локально конечный бесконечный граф является счетным.

Помимо этого, на бесконечный граф можно перенести понятие маршрута, причем тремя различными способами:

1. Конечный маршрут в определяется так. Маршрутом в данном графе называется конечная последовательность ребер вида , . Маршрут можно обозначить и так: .

2. Бесконечным в одну сторону маршрутом в с начальной вершиной называется бесконечная последовательность ребер вида , .

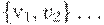3. Бесконечным в обе стороны маршрутом в графе называется бесконечная последовательность ребер вида ,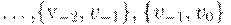

Бесконечные в одну сторону и в обе стороны цепи и простые цепи определяются очевидным образом, так же как и понятия длины цепи и расстояния между вершинами. Бесконечные простые цепи не так уж трудно обнаружить.

Теорема 6.1. (Кениг, 1936) Пусть — связный локально конечный бесконечный граф, тогда для любой вершины 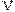существует бесконечная в одну сторону простая цепь с начальной вершиной .

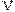Доказательство

Если — произвольная вершина графа , отличная от 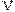, то существует нетривиальная простая цепь от 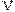до , отсюда следует, что в имеется бесконечно много простых цепей с начальной вершиной 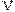. Поскольку степень 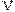конечна, то бесконечное множество таких простых цепей должно начинаться с одного и того же ребра. Если таким ребром является , то, повторяя эту процедуру для вершины , получим новую вершину и соответствующее ей ребро . Продолжая таким образом, получим бесконечную в одну сторону простую цепь .

Важное значение леммы Кенига состоит в том, что она позволяет получить результаты о бесконечных графах из соответствующих результатов для конечных графов. Типичным примером является следующая теорема.

Теорема 6.2. Пусть — счетный граф, каждый конечный подграф которого планарен, тогда и планарен.

Доказательство Так как — счетный граф, его вершины можно занумеровать в последовательность . Исходя из нее, построим строго возрастающую последовательность подграфов графа , выбирая в качестве подграф с вершинами и ребрами графа , соединяющими только эти вершины между собой. Далее, примем на веру тот факт, что графы могут быть уложены на плоскости конечным числом, скажем , топологически различных способов, и построим еще один бесконечный граф . Его вершины , пусть соответствуют различным укладкам графов , а его ребра соединяют те из вершин и , для которых и плоская укладка, соответствующей . Мы видим, что граф связен и локально конечен, поэтому, как следует из леммы Кенига, он содержит бесконечную в одну сторону простую цепь. А так как граф является счетным, то эта бесконечная простая цепь и дает требуемую плоскую укладку графа .

Стоит подчеркнуть, что если принять дальнейшие аксиомы теории множеств, в частности, аксиому выбора для несчетных множеств, то многие результаты можно перенести и на такие бесконечные графы, которые необязательно являются счетными.

Задание

1. Изобразить конечные и бесконечные графы.

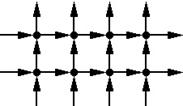
2. Определите, какие графы изображены

A	B
C	D
E	F

Проверьте правильность ответа: A, b – платоновы тела; c – неориентированный конечный однородный граф степени 2; d – неориентированный конечный однородный граф степени 1; е – неориентированный конечный однородный граф степени 4; f – ориентированный бесконечный однородный граф степени 2

Порядок выполнения работы:

1. Выполнить задание.

2. Оформить отчет.

Содержание отчета:

1. Тема.

2. Цель.

3. Задачи.

4. Материальное обеспечение.

5. Практическое задание.

Вопросы для самоконтроля:

1. Дайте определение конечного графа.

2. Дайте определение бесконечного графа.

3. Какой граф называется однородным?

4. Где применяются бесконечные графы?

Практическая работа № 5

Тема: Решение задач по теории графов

Цель: научиться применять математический аппарат теории графов в решении задач.

Задачи:

1.Закрепить знания основных понятий теории конечных и бесконечных графов.

2. Использовать математический аппарат теории графов

Материальное обеспечение: раздаточный материал.

Теоретическая часть:

Под графом мы будем понимать множество точек (вершин), некоторые из которых соединены отрезками (ребрами).

Степень вершины графа — это количество выходящих из нее (или, что то же самое, входящих в нее) ребер (еще говорят: количество ребер, инцидентных данной вершине). Вершина графа называется четной, если ее степень четна, и нечетной в противном случае.

Некоторая часть вершин данного графа называется компонентой связности, если из любой ее вершины можно «дойти» до любой другой, двигаясь по ребрам.

В некоторых случаях на ребрах графа выбирается «направление движения» (например, когда на автомобильной дороге вводится одностороннее движение). При этом получается ориентированный граф. (Если направление движения по ребрам не определено, то граф называется неориентированным). В ориентированном графе различают положительную и отрицательную степень каждой вершины (то есть количество ребер, соответственно, входящих и выходящих из нее). Две вершины могут быть соединены и несколькими ребрами, направления движения по которым противоположны («дорога с двусторонним движением»). Изменяется понятие компоненты связности: теперь каждый «маршрут» от одной вершины до другой должен учитывать направление движения по ребрам.

Графовые задачи обладают рядом достоинств, позволяющих их использовать для развития воображения и улучшения логического мышления, применимы в решении многих геометрических задач.

На уроке геометрии было предложено построить граф классификации геометрических объектов. Это оказалось легко сделать с помощью понятия граф.

Задача о мостах

Бывший Кенигсберг (ныне Калининград) расположен на реке Прегель. В пределах города река омывает два острова. С берегов на острова были перекинуты мосты. Старые мосты не сохранились, но осталась карта города, где они изображены.

Издавна среди жителей Кёнигсберга была распространена такая загадка: как пройти по всем мостам, не проходя ни по одному из них дважды? Многие кёнигсбержцы пытались решить эту задачу как теоретически, так и практически, во время прогулок. Но никому это не удавалось, однако не удавалось и доказать, что это даже теоретически невозможно.

Этот вопрос привлек внимание ученых разных стран. В 1736 году задача о семи мостах заинтересовала выдающегося математика, члена Петербургской академии наук Леонарда Эйлера, о чём он написал в письме итальянскому математику и инженеру Мариони от 13 марта 1736 года. В этом письме Эйлер пишет о том, что он смог найти правило, пользуясь которым легко определить, можно ли пройти по всем мостам, не проходя дважды ни по одному из них (в случае семи мостов Кёнигсберга это невозможно).

Причем, он не только решил эту конкретную задачу, но придумал общий метод решения подобных задач. Эйлер поступил следующим образом: он «сжал» сушу в точки, а мосты « вытянул» в линии, как показано на рисунке 1 а, б.

Рисунок 1

На упрощённой схеме части города (графе) мостам соответствуют линии (рёбра графа), а частям города — точки соединения линий (вершины графа). В ходе рассуждений Эйлер пришёл к следующим выводам:

Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа всегда чётно. Невозможно начертить граф, который имел бы нечётное число нечётных вершин.

Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.

Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.

Давайте четко сформулируем поставленную задачу. При каком условии можно обойти все ребра графа, пройдя каждое ровно один раз? Решение оказалось очень простым. Сосчитаем, сколько ребер выходит из каждой вершины. Одни из этих чисел будут четными, а другие - нечетными. Будем и сами вершины называть четными, если из них выходит четное число ребер, и нечетными в противном случае. Как мы уже знаем: количество ребер, выходящих из данной вершины, называется степенью вершины. Вершина графа, имеющая нечетную степень, называется нечетной, а четную степень – четной.

Граф кёнигсбергских мостов имел четыре нечётные вершины, следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды.

Решая задачу про кенигсбергские мосты, Эйлер установил, в частности, свойства графа:

v Если все вершины графа четные, то можно одним росчерком (т.е. не отрывая карандаша от бумаги и не проводя дважды по одной и той же линии) начертить граф. При этом движение можно начать с любой вершины и окончить в той же вершине.

v Граф с двумя нечетными вершинами тоже можно начертить одним росчерком. Движение надо начинать от любой нечетной вершины, а закончить на другой нечетной вершине.

v Граф с более чем двумя нечетными вершинами невозможно начертить одним росчерком.

В задаче о кенигсбергских мостах все четыре вершины соответствующего графа нечетные, то есть нельзя пройти по всем мостам один раз и закончить путь там, где он был начат.

Задачи:

1. Между девятью планетами Cолнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля — Меркурий, Плутон — Венера, Земля — Плутон, Плутон — Меркурий, Меркурий — Венера, Уран — Нептун, Нептун — Сатурн, Сатурн — Юпитер, Юпитер — Марс и Марс — Уран. По каждому маршруту ракеты летают в обе стороны. Можно ли долететь на рейсовых ракетах от Земли до Марса?

2. В государстве 100 городов. Из каждого города выходит 4 дороги. Сколько всего дорог в государстве?

3. Экспозиция картинной галереи представляет собой систему коридоров, на обеих стенах которых развешаны картины:

Можно ли предложить такой маршрут осмотра экспозиции, при котором

посетитель проходит вдоль каждой стены ровно один раз?

4. В городе 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединён ровно с пятью другими?

5. В теннисном турнире каждый игрок команды «синих» встречается с каждым игроком команды «красных». Число игроков в командах одинаково и не больше восьми. «Синие» выиграли в четыре раза больше встреч, чем «красные». Сколько человек в каждой из команд?

6. Можно ли прогуляться по парку и его окрестностям так, чтобы при этом перелезть через каждый забор ровно один раз?

7. Можно ли нарисовать граф, изображённый на рисунках а,б

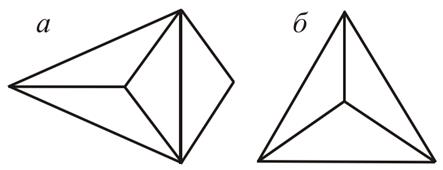
не отрывая карандаша от бумаги и проводя каждое ребро ровно один раз?

8. Дан кусок проволоки длиной 120 см.

Можно ли, не ломая проволоки, изготовить каркас куба с ребром 10 см? Какое наименьшее число раз придётся ломать проволоку, чтобы всё же изготовить требуемый каркас?

9. Можно ли так нарисовать 5 горизонтальных и 4 вертикальных отрезка, чтобы каждый горизонтальный отрезок пересекался ровно с тремя вертикальными, а каждый вертикальный ровно с тремя горизонтальными?

10. При встрече каждый из моих одноклассников пожал руку другому (каждый пожал каждому). Сколько рукопожатий было сделано, если друзей было: 1)трое; 2)четверо; 3)пятеро? (решите и изобразите граф решения)

Порядок выполнения работы:

1. Решить задачи.

2. Оформить отчет.

Содержание отчета:

1. Тема.

2. Цель.

3. Задачи.

4. Материальное обеспечение.

5. Практическое задание.

Вопросы для самоконтроля:

1. Как в задачах применяется ориентированный граф?

2. Какой граф можно начертить, не отрывая карандаша от бумаги, при этом можно начинать с любой вершины графа и завершить его в той же вершине?

3. Какое современное устройство решает задачу о кинесберских мостах?

4. Когда вершина графа называется четной, а когда нечетной?

Практическая работа № 6

Тема: Решение задач по теории графов. Алгоритм Краскаля»

Цель: изучить и отработать навыки в применении алгоритма Краскала; закрепить навыки моделирования графов в графической среде Kraskal.

Задачи:

1. Закрепить знания основных понятий теории графов.

2. Приобрести практические умения использования специального программного обеспечения для моделирования.

3. Использовать математический аппарат теории графов

Материальное обеспечение:

Программы для вычисления алгоритма краскала: Kraskal

Теоретическая часть:

Остов графа (стягивающее дерево, spanning tree, ST) – дерево, полученное из графа, выбрасыванием части ребер.

Минимальный остов графа (стягивающее дерево минимального веса, Minimal Spanning Tree, MST) – остов, с минимальной суммой весов входящих в него ребер.

Алгоритм Краскала вычисляет для заданного взвешенного неориентированного графа остовное дерево с наименьшей суммой весов ребер— остовное дерево наименьшего веса. В новой задаче множество вершин при поиске остовного дерева наименьшего веса не меняется.

Дата добавления: 2019-02-22; просмотров: 4385; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 7 8 9 Следующая ⇒

Мы поможем в написании ваших работ!