Компоненты связного и несвязного графа
В теории графов, понятие связности графа является ключевым при решении многих прикладных задач.
Определение связного и несвязного графа.
Граф G(V,E) называется связным, если для любой пары различных вершин этого графа существует цепь, соединяющая эти вершины. Если для графа G(V,E) можно указать пару различных вершин, которые не соединяются цепью, то граф называется несвязным.
Пример связного и несвязного графов.
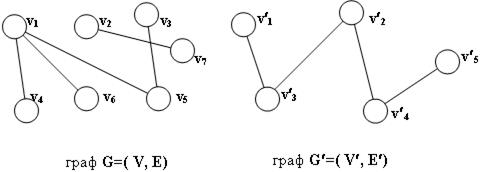
Компонента связности графа — некоторое множество вершин графа такое, что для любых двух вершин из этого множества существует путь из одной в другую, и не существует пути из вершины этого множества в вершину не из этого множества.
Для ориентированных графов определено понятие сильной компоненты связности
Пример компонент связности графа.
Рассмотрим пример двусвязного графа G(V, E). Всего имеется два множества связных между собой вершин V1 = {v1, v2, v5, v6} и V2 = {v3, v4, v7, v8}.
Свойства компонент связности.
1. Каждая вершина графа входит лишь в одну компоненту связности.
2. Любой конечный граф имеет конечное число компонент связности.
3. Граф, состоящий из единственной компоненты связности, является связным.
4. Каждая компонента связности графа является его подграфом.
Теорема. Если в конечном графе G ровно две вершины u и v имеют нечетную степень, то они связаны.
Задание 1. Компоненты сильной связности ориентированного графа.
С помощью матрицы смежности найти компоненты сильной связности ориентированного графа D .
|
|
|
Cоставляем матрицу смежности A(D) размерности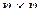 
(n− количество вершин) для данного ориентированного графа: она состоит из нулей и единиц, номера строк – индексы вершин , из которых исходят дуги, номера столбцов – индексы вершин, в которые дуги входят (если есть дуга, исходящая из вершины vi и входящая в vj, то элемент матрицы смежности, стоящий на пересечении i-той строки и j-того столбца равен 1, иначе – 0.).
Для того, чтобы выделить компоненты сильной связности, необходимо сначала найти матрицу достижимости T(D)
Матрица достижимости ориентированного графа D − квадратная матрица T(D)=[tij] порядка n, элементы которой равны
ориентированного графа по (1) формуле (T(D)=sign[E+A+A2+A3+… An-1]), затем находим матрицу сильной связности S(D) ориентированного графа (она должна быть симметрической) по (2) формуле (S(D)=T(D)&TT(D) (TT-транспонированная матрица, &- поэлементное умножение)).
Алгоритм выделения компонент сильной связности
1. Присваиваем p=1 (p − количество компонент связности), 
.
2. Включаем в множество вершин Vp компоненты сильной связности Dp вершины, соответствующие единицам первой строки матрицы Sp . В качестве матрицы A(Dp) возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из Vp.
|
|
|
3. Вычеркиваем из Sp строки и столбцы, соответствующие вершинам из Vp. Если не остается ни одной строки (и столбца), то p- количество компонент сильной связности. В противном случае обозначим оставшуюся после вычеркивания срок и столбцов матрицу как Sp +1, присваиваем p = p+1 и переходим к п. 2.
Пример выполнения задания 1
Выделим компоненты связности ориентированного графа, изображенного на рисунке 1. В данной задаче количество вершин n =5.
Рисунке 1.
Значит, для данного ориентированного графа матрица смежности будет иметь размерность 5×5 и будет выглядеть следующим образом
.
Найдем матрицу достижимости для данного ориентированного графа по формуле (1)
, 
,
,
Следовательно,
.
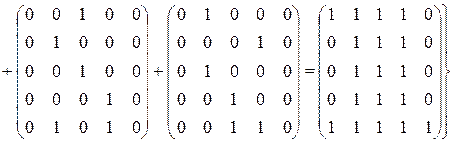Таким образом, матрица сильной связности, полученная по формуле (2), будет следующей:
.
Присваиваем p=1 и составляем множество вершин первой компоненты сильной связности D1: это те вершины, которым соответствуют единицы в первой строке матрицы S(D). Таким образом, первая компонента сильной связности состоит из одной вершины 
.
|
|
|
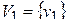Вычеркиваем из матрицы S1(D) строку и столбец, соответствующие вершине v1, чтобы получить матрицу S2(D):
.
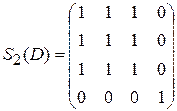Присваиваем p=2. Множество вершин второй компоненты связности составят те вершины, которым соответствуют единицы в первой строке матрицы S2(D), то есть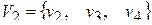 
. Составляем матрицу смежности для компоненты сильной связности 
исходного графа D − в ее качестве возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из V2:
.
Вычеркиваем из матрицы S2(D) строки и столбцы, соответствующие вершинам из V2 ,чтобы получить матрицу S3(D), которая состоит из одного элемента:
и присваиваем p=3. Таким образом, третья компонента сильной связности исходного графа, как и первая, состоит из одной вершины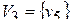 
.
Таким образом, выделены 3 компоненты сильной связности ориентированного графа D:
Дата добавления: 2019-02-22; просмотров: 1149; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!