Минимальный остов графа. Дан взвешенный граф.

 

Строим граф, присоединяя к пустому графу на множестве вершин заданного графа ребро наименьшего веса. К полученному графу последовательно присоединяем остальные ребра, выбирая на каждом шаге ребро наименьшего веса, не образующее цикл с имеющимися ребрами. В нашем случае начинаем с ребра весом 13 – наименьшего в графе. На рисунках дана последовательность действий. Ребро весом 19 не включается в остов, так как оно образует цикл с ребрами

весом 14 и 13.

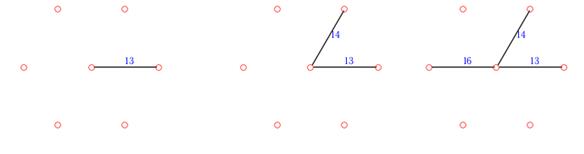
Выполнение алгоритма Краскала:

1. Начальная фаза. Минимальный покрывающий лес пуст.

2. Перебираем ребра в порядке возрастания веса: первое ребро с весом 2. Добавляем его к А.

3. Следующее безопасное ребро с весом 6. Добавляем его.

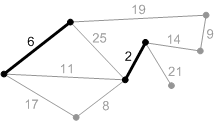
4-8. Добавляем остальные безопасные ребра.

 

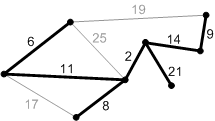
Пример выполнения алгоритма Краскаля. Заштрихованные ребра принадлежат растущему лесу.

 

Изучить инструкцию к практической работе.

Для запуска программы необходимо активировать exe – файл с названием «Краскал.exe» запустится программа. Рисунок главной формы изображен на ри­сунке.

На главной форме программы изображены: текстовое поле необходимое для ввода количество узлов графа, для которого нужно будет найти остов мини­мального веса, затем нужно нажать кнопку «ОК». Далее нужно занести веса в матрицу весов «Дано» вводить нужно только по горизонтали, а по вертикали программа заполнит поля автоматически. Далее нужно расставить узлы нашего графа, для этого одним щелчком по полю «Данный граф» создастся узел, он бу­дет помечен синей точкой аналогично выполнить для остальных вершин графа. Также узлы можно расставить случайным образом, для этого нужно пометить флажок «Разместить узлы случайно» и нажать кнопку «Рисовать» при каждом нажатии на кнопку вершины будут размещаться случайно.

 

 

После того, когда граф на рисован необходимо найти «Остов минималь­ного веса» с помощью алгоритма Краскала, для этого нажимать кнопку «Вычис­лить». Остов минимального веса будет изображен в поле «Полученный мини­мальный остов» и в поле «Результат» будет показан результат виде матрицы ве­сов.

Задание:

Проработать две первые задачи. Третью и четвертую решить самостоятельно,  используя программное обеспечение Kraskal .

 

Задача №1 . Дан взвешенный связный неориентированный граф, состоя­щий из пяти вершин. Необходимо найти остов минимального веса с помощью ал­горитма Краскала.

	Выбираем вершину начала построения остова минимального веса, напри­мер, первую вершину.
	Шаг 1. Найдено ребро минимального веса: 1-2=6. Полученный остов на рисунок.
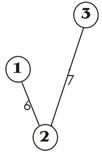
	Шаг 2. Найдено ребро минимального веса: 2-3=7. Полученный остов на рисунок.
	Шаг 3. Найдено ребро минимального веса: 3-4=9. Полученный остов на рисунок.
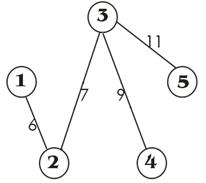
	Шаг 4. Найдено ребро минимального веса: 3-5=11. Рассмотрены все вершины и инцидентные ребра этим вершинам, остав­шиеся образуют цикл в полученном минимальном остове. А это не удовлетворяет условиям поставленной задачи. На четвертом шаге получили окончательный остов минимального веса, ко­торый представлен на рисунке.

При изменении вершины начала построения конфигурация остова мини­мального веса не измениться, а измениться лишь последовательность построения ребер остова.

Например, если в качестве начальной вершины выбрать четвертую вер­шину, то последовательность этапов построения остова минимального веса будет выглядеть следующим образом:

Шаг 1. 4-3=9;

Шаг 2. 3-2=7;

Шаг 3. 2-1=6;

Шаг 4. 3-5=11;

При этом конфигурация остова останется прежней. Решим данную задачу с помощью программной модели. Чтобы решить данную задачу необходимо по­строить матрицу весов, матрица представлена на рисунке.

Матрица весов

Полученный минимальный остов с помощью программной модели изо­бражен на рисунке.

Полученный минимальный остов

После проверки вычислений вручную и программной модели результат одинаковый, это означает, что программная модель работает и функционирует верно.

 

Задача №2. Дан взвешенный, связный, неориентированный граф, состоя­щий из девяти вершин. Необходимо найти остов минимального веса с помощью ал­горитма Краскала. Исходный граф на рисунке.

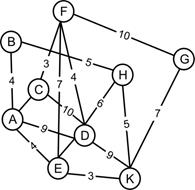
	Выбираем вершину начала построения остова минимального веса, напри­мер, первую вершину.
	Шаг 1. Найдено ребро минимального веса: AC=1. Полученный остов на рисунок.
	Шаг 2. Найдено ребро минимального веса: CF=3, AB=4, AC=4. Полученный остов на рисунок.
	Шаг 3. Найдено ребро минимального веса: FD=4, EK=3, AE=4. Полученный остов на рисунок.
	Шаг 4. Найдено ребро минимального веса: KH=5, KG=4. Рассмотрены все вершины и инцидентные ребра этим вершинам, остав­шиеся ребра образуют цикл в полученном минимальном остове. А это не удовлетворяет условиям поставленной задачи. На четвертом шаге получен окончательный остов минимального веса, ко­торый представлен на рисунке.

 

Решим данную задачу с помощью программной модели. Чтобы решить данную задачу необходимо по­строить матрицу весов.

Таблица 1. Матрица весов

	A	B	C	D	E	F	G	H	K
A	-	4	1	9	4	-	-	-	-
B	4	-	-	-	-	-	-	5	-
C	1	-	-	10	-	3	-	-	-
D	9	-	10	-	5	4	-	6	9
E	4	-	-	5	-	7	-	-	3
F	-	-	3	4	7	-	10	-	-
G	-	-	-	-	-	10	-	-	7
H	-	5	-	6	-	-	-	-	5
K	-	-	-	9	3	-	7	5	-

 

Полученный минимальный остов с помощью программной модели изо­бражен на рисунке.

Остов минимального веса

       После проверки вычислений вручную и программной модели полученные остовы минимального веса различаются, но они построены верно. Это связано с тем, что программа выбирает другую вершину начала. После решения двух контрольных задач стало ясно, что разработанная программная модель работает верно.

 

Задача №3. Найти остов минимального веса с помощью алгоритма Краскала., проверить программой Краскала.

Задача №4. Найти минимальное остовное дерево в неориентированном нагруженном графе. Результат проверить программным обеспечением.

а)	б)	в)

Порядок выполнения работы:

1. Изучить инструкцию к практической работе.

2. Выполнить задание.

3. Оформить отчет.

 

Содержание отчета:

1. Тема.

2. Цель.

3. Задачи.

4. Материальное обеспечение.

5. Практическое задание.

 

Вопросы для самоконтроля:

1. Дайте определение остов графа.

2. Дайте определение минимальный остов графа.

3. В чем смысл алгоритма Краскала?

 

 

Практическая работа № 7

Тема: Решение задач по теории графов.  Двойственность по Уитни

Цель: изучить теоретические основы планарности, двойственности графов и теорему Уитни; закрепить навыки моделирования графов.

Задачи:

1. Закрепить знания основных понятий теории графов.

2. Использовать математический аппарат теории графов

Материальное обеспечение:

Раздаточный материал. Линейка карандаш.

Теоретическая часть:

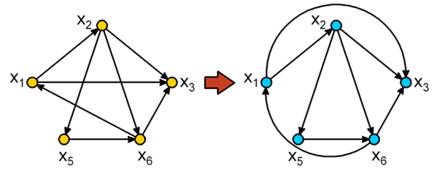
	Граф G =(V, E), который может быть изображен на плоскости или сфере без пересечений называется планарным
	На рисунке показаны непланарные графы. Эти два графа играют важную роль в теории планарных графов и известны как графы Куратовского.

Неориентированный граф G = (V, E) называют двудольным, если множество его вершин V может быть разбито на такие два подмножества V^а и V^b, что каждое ребро имеет один конец в V^а , а другой в V^b (рисунок 1,а).

Ориентированный граф G называется двудольным, если его неориентированный двойник – двудольный граф (рисунок 1,б,в).

Двудольный граф G=(V^а∪V^b, E) называют полным, если для любых двух вершин v_i∈V^а и v_j ∈V^b существует ребро (v_i,v_j) в G=(V,E) (рисунок 1,г).

Рисунок 1

Теорема ( X . Уитни, 1932 г.). Граф планарен тогда и только тогда когда он имеет абстрактно двой­ственный граф.

Говорят, что граф G укладывается на поверхности S, если его можно нарисовать на этой поверхности так, что его ребра будут пересекаться лишь в концевых точках - вершинах. Граф называется планарным, если его можно уложить на плоскости. Изображение планарного графа на плоскости называют планарной укладкой. Для каждого простого планарного графа существует планарная укладка, в которой все ребра графа будут прямыми линиями.

Если граф не укладывается на плоскости (поверхности нулевого порядка), то его можно уложить на какой - либо другой поверхности (более высокого порядка). Укладываемость графа на плоскости равносильна его укладываемости на сфере, поскольку сфера и плоскость относятся к поверхности нулевого порядка, что можно установить стереографической проекцией сферы на плоскость.

На рисунок 2, а и б показаны две планарные укладки одного и того же графа, а на рисунке  в и г приведены два основных непланарных графа – K₅ и K_3,3 (графы Куратовского).

Графы Куратовского считаются основными непланарнами графами потому, что играют решающую роль в исследовании планарности графов.

Теорема Граф планарен тогда и только тогда, когда каждый его блок планарен.

Рисунок 2. Примеры планарного и непланарных графов:
а - планарная укладка с непрямолинейными ребрами;
б - планарная укладка того же графа с прямолинейными ребрами;
в - непланарный граф K₅; г - непланарный граф K_3,3

 

До появления статьи Куратовского, в которой был дан критерий планарности графов, характеризация планарных графов была труднейшей нерешенной проблемой. Доказательство приводимой ниже теоремы Куратовского можно найти в книге.

Рисунок 3. Непланарность графа Петерсена: а - граф Петерсена;
б - граф Петерсена, стянутый к K₅;
в - один из подграфов графа Петерсена, гомеоморфный K_3,3

 

Граф Петерсена не имеет подграфов, гомеоморфных K₅, но легко стягивается к K₅. Сложнее увидеть, что граф Петерсена имеет подграф, гомеоморфный K_3,3.

Уитни связал планарность графов с существованием двойственных графов. Граф G* называется двойственным к графу G, если существует такое взаимнооднозначное соответствие их ребер, что множество ребер графа G* образует цикл тогда и только тогда, когда в графе G это же множество ребер образует разрезающее множество. Для плоского графа существует простой способ построения двойственного графа (см. пример на рисунок 4).

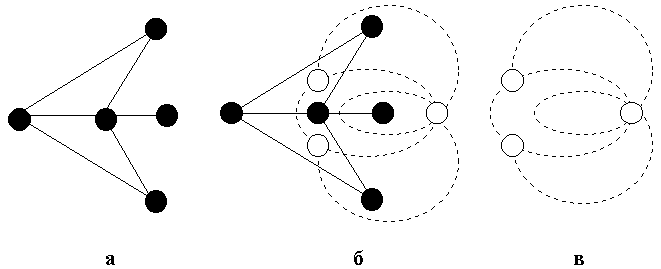
Рисунок 4. Пример: а – граф G; б – построение двойственного графа G*;
в – граф G*, двойственный графу G

Суть способа построения в следующем: а) в каждой области укладки графа G на плоскости размещается вершина графа G*; б) через каждое ребро eграфа G, общее для областей 0_i и 0_j, проводится линия, соединяющая вершины и и образующая ребро e*.

Теорема Граф имеет двойственный граф тогда и только тогда, когда он планарен.

Задание:

1. Постройте планарный граф с а) 6; б) 7; в) 8; г) 9; вершинами так, чтобы некоторые его ребра пересекались.

2. Постройте плоский граф, соответствующий графу из предыдущего задания.

3. Постройте геометрически двойственный граф к графу из задания 2.

4. Покажите, что К₅ не обладает абстрактно двойственными графами.

Порядок выполнения работы:

1. Изучить инструкцию к практической работе.

2. Выполнить задание.

3. Оформить отчет.

 

Содержание отчета:

1. Тема.

2. Цель.

3. Задачи.

4. Материальное обеспечение.

5. Практическое задание.

 

Вопросы для самоконтроля:

1. Дайте определение планарности графа.

2. Какой используется граф, в определении двудольного графа?

3. Какие два вида графа рассматриваются в теореме Х. Уитни?

4. Что означает укладка графа на поверхности?

 

Практическая работа № 8

Тема: Решение задач по теории графов.

Построение матриц смежностей и инциденций

 

Цель: изучение матричных способов представления графов; отработать на примерах основные понятия теории графов; научить строить графы по матрице смежности; по графу составлять матрицу смежности; закрепить навыки моделирования графов в графической среде Grafoanalizator1.3.3 rus.

Задачи:

1. Закрепить знания основных понятий теории графов.

2. Приобрести практические умения использования специального программного обеспечения для моделирования.

3. Использовать математический аппарат теории графов

Материальное обеспечение:

Программы для графического представления графов: Grafoanalizator1.3.3 rus, Просто граф, практическая работа.

Теоретическая часть:

Матрица смежности

Пусть дан граф G, его матрица смежности обозначается через A=[a_ij]и определяется следующим образом:

a_ij=1, если в G существует дуга (x_i,x_j),

a_ij=0, если в G нет дуги (x_i,x_j).

 

 

Таким образом, матрица смежности графа, изображенного на рисунке 1, имеет вид

 

 

 

 

 

Матрица смежности полностью определяет структуру графа. Например, сумма всех элементов строки x_i матрицы дает полустепень исхода вершины x_i, а сумма элементов столбца x_i - полустепень захода вершины x_i. Множество столбцов, имеющих 1 в строке x_i есть множество Г(x_i), а множество строк, которые имеют 1 в столбце x_i совпадает с множеством Г^-1(x_i).

Петли на графе представляют собой элементы, имеющие 1 на главной диагонали матрицы, например a₂₂, a₆₆ для графа, изображенного на рисунке 1.

В случае неориентированного графа матрица смежности является симметричной относительно главной диагонали (рисунок 2).

 

 

Матрица инцидентности

Пусть дан граф G с n вершинами и m дугами. Матрица инцидентности графа G обозначается через B=[b_ij] и является матрицей размерности n x m, определяемой следующим образом:

b_ij=1, если x_i является начальной вершиной дуги a_j;

b_ij=-1, если x_i является конечной вершиной дуги a_j;

b_ij=0, если x_i не является концевой вершиной дуги a_j.

Для графа, приведенного на рисунке 1, матрица инцидентности имеет вид:

 

Поскольку каждая дуга инцидентна двум различным вершинам (за исключением случая, когда дуга образует петлю), то каждый столбец содержит один элемент, равный 1, и один - равный -1. Петля в матрице инцидентности не имеет адекватного математического представления (в программной реализации допустимо задание одного элемента b_ij=1).

Если G является неориентированным графом (рисунок 2), то его матрица инцидентности определяется следующим образом:

b_ij=1, если x_i является концевой вершиной дуги a_j;

b_ij=0, если x_i не является концевой вершиной дуги a_j.

 

Матрица инцидентности, как способ задания графов, успешно применяется при описании мультиграфов (графов, в которых смежные вершины могут соединяться несколькими параллельными дугами).

---

Дата добавления: 2019-02-22; просмотров: 2229; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!