АБСТРАКТНО-ДЕДУКТИВНИЙ І КОНКРЕТНО – ІНДУКТИВНИЙ МЕТОДИ НАВЧАННЯ
У навчанні математики неабиякого поширення набули абстрактно-дедуктивний і конкретно - індуктивний методи навчання. Вперше докладно проаналізував ці методи в методиці навчання математики К. Ф. Лебединцев.
Суть абстрактно-дедуктивного методу навчання полягає в тому, що під час вивчення нового матеріалу вчитель відразу сам повідомляє означення понять, що вводяться, а потім наводить конкретні приклади об'єктів, що належать до понять. Формулюється й доводиться теорема, і лише після цього розглядаються конкретні приклади застосування нового теоретичного матеріалу.
Конкретно-індуктивний метод, навчання протилежний абстрактно-дедуктивному методу. Під час навчання цим методом пояснення нового матеріалу починається з розгляду прикладів. Використовуючи приклади, учні мають можливість виділити суттєві ознаки поняття, що вводиться. Це допомагає самостійно чи з допомогою вчителя сформулювати означення поняття. Рисунок до теореми дасть змогу учням виявити властивості зображеної фігури і самостійно чи з допомогою вчителя сформулювати теорему.
Математичні поняття.
Кожна наука оперує своїми поняттями. За допом. понять ми виражаємо заг., істотні ознаки предметів і явищ, процесів і відносин об'єктивної дійсності. У математичних поняттях відображаються в осн. кількісні відносини і просторові форми матеріального світу.
Кожне поняття характеризується об'ємом і змістом.
|
|
|
Об'єм поняття– це множина об'єктів, на які розповсюджується дане поняття. Зміст поняття – це сукупність основних ознак об'єктів, що охоплюються цим поняттям. Зміст поняття розкривається за допомогою визначення, об'єм – за допом. класифікації. За допом. визначення і класифік. окр. поняття організовуються в с-му взаємозв'яз. понять.
У ШКМ уміння вказати об'єм поняття виявляється за допом. завдань типу: наведіть приклади різних трикутників, а уміння вказати зміст - за допом. завдань типу: що називається трикутником? Між об'ємом і змістом має місце закон зворотного відношення: чим ширше зміст поняття, тим вужчий його об'єм і, навпаки. Наприклад, поняття «трикутник». Додамо до 2-х його ознак: 1)плоский многокутник; 2)наявність 3-х сторін. Ще третю: 3) 2 сторони рівні. Отримали нове поняття «рівнобедрений трикутник». Зміст ширший, а об'єм вужче: множина рівнобедр. трикутників є підмнож. м-ни трикутників взагалі.
Формування понять– складний психологічний процес, що зазвичай протікає по такій схемі: відчуття – сприйняття – уявлення – поняття.Поняття абстрагується від індивід. рис і є рез-том узагальнення сприйняття і представлення вел. к-ті однорідних предметів і явищ. Завершальним етапом формування поняття, як прав., є його визначення.
|
|
|
Перерахування необх. і достатніх ознак поняття, зведених в зв'язну пропозицію, є визначення поняття. У ШКМ визначення розглядають як математичну пропозицію, яка зводить дане поняття мат-ки до вже знайомих мат-них понять. Необх., щоб учні розуміли, що ніякі визначення не доводяться. Про визначення не має сенсу говорити, істинне воно або хибне. Визначення м.б. правильним (коректним) або неправильним (некоректним) залежно від того, задовольняє воно чи ні певним вимогам (відсутність порочного круга і відсутність омонімії).
У математиці і в навчанні математики застосовуються різні способи визначень.
І. «Через найближчий ряд і видову відмінність».Наприклад, означення поняття «квадратне рівняння» – рівняння (рід) + вигляду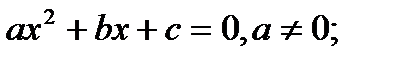 
«ромб» - паралелограм (рід) + сторони якого рівні (видова відмінність). Такі визначення дозволяють замінити при необхідності, наприклад, при доказі теорем, одне поняття іншим.
ІІ. Генетично(спосіб, вказуючий на походження поняття). Наприклад, визначення кола, круга, сфери, кулі, лінійного кута, двогранного кута, конуса, циліндра як тіл обертання – генетичні. Проте не всі математичні поняття визначаються таким чином. Процес зведення одного поняття до інших не може бути нескінченним. Тому є первинні поняття, які явно не визначаються через інші поняття, їх властивості виражаються в аксіомах, це неявні аксіоматичні визначення понять, наприклад, точка, пряма, площина, натуральне число
|
|
|
Математичні речення.
Кожна математична теорія являє собою безліч речень, що описують якусь структуру (якщо ця теорія викладається змістовно в певній конкретній інтерпретації) або якийсь аксіоматичний клас структур (якщо вона викладається абстрактно поза всякої інтерпретації).
Належність речень до деякої математичної теорії визначається двома ознаками: (а) речення записано (або сформульовано) на мові даної теорії, складається з математичних (що належать мови теорії) і логічних термінів або символів і не містить ніяких інших термінів або символів; (Б) речення істинне, тобто є або вихідним істинним реченням (аксіомою) даної теорії, або його істинність встановлюється доказом за допомогою вже відомих (вихідних або раніше доведених) істинних тверджень.
З кожним математичним реченням пов'язані зміст і логічна форма (або структура).
|
|
|
Подання, що можна обмежитися в навчанні математики лише розкриттям змісту кожного математичного речення, помилкове. Зміст нерозривно пов'язаний з формою, і не можна осмислити перше без розуміння другого.
Так як одна з центральних задач навчання математики полягає в навчанні встановлення істинності математичних речень (найчастіше за допомогою доказів), а істинне значення цих реченнь залежать від їх логічної структури, то природно вважати одним із завдань методики викладання математики розкриття логічної структури математичних речень.
Будь-яке математичне (і не тільки математичне) речення або елементарне, тобто розчленовується на частини, кожна з яких в свою чергу є реченням, або побудовано з елементарних, певним чином з'єднаних між собою логічними зв'язками.
Сукупність і порядок логічних зв'язків, за допомогою яких складне речення утворене з елементарних, становить логічну структуру цього складного речення.
Без розуміння точного сенсу логічних зв'язків не може бути досягнуто і правильне розуміння точного сенсу всієї логіко-математичної конструкції, тобто математичного речення, утвореного з їх допомогою, а отже, і вираженого в ньому математичного змісту.
Відношення рівносильности і слідування між реченнями знаходять широкі застосування в математиці і в навчанні математики. Перше з цих відншень зводиться до другого, а відношення слідування є основою будь-яких доказів.
Математичні доведення.
В математиці доведенням називається ланцюжок логічних умовиводів, який показує, що при якомусь наборі аксіом і правил виведення вірно деяке твердження. Тобто кажучи «математичне доведення», ми маємо на увазі доказ математичного речення.
У шкільному курсі математики учні ознайомлюються з такими основними методами доведень: синтетичним, аналітичним, аналітико-синтетичним (його інколи називають методом руху з двох кінців), методом доведення від супротивного, повної індукції, математичної індукції, методами геометричних перетворень (центральна симетрія, осьова симетрія, поворот, паралельне перенесення, гомотетія та подібність), алгебраїчним методом, окремими випадками якого є векторний і координатний. У сучасному шкільному курсі застосовано також методи математичного аналізу: метод границь, методи диференціального та інтегрального числення.
+Аналітичний метод. Міркування виконуються від того, що потрібно довести. При цьому з припущення правильності того, що слід довести (основа), виводяться наслідки, які приводять до очевидної правильної нерівності (наслідку).
+Синтетичний метод. У ньому міркування ведуться від умови або від уже відомого твердження до того, що доводіться. Суть цього методу полягає втому, що необхідне доведення виводиться за допомогою вже відомих (доведених) тверджень.
Логічною основою аналітичного методу, як і синтетичного, є аксіома: з правильного твердження завжди випливає правильний наслідок.
+Аналітико-синтетичний метод. Цей метод полягає в тому, що пошук доведення починають аналітичним методом, але міркування не доводять до кінця, а, спиняючись на певному кроці, починають міркувати у зворотному напрямі, тобто з розгортання умови. Отже, завершують доведення синтетичним методом.
+Метод доведення від супротивного. Цей метод уводять уже в 7 класі напочатку навчання курсу планіметрії. Його логічною основою є закон виключення третього: з двох супротивних тверджень одне завжди правильне, друге - неправильне, а третього бути не може. Завдяки цьому закону замість доведення певного твердження під час використання методу доведення від супротивного доводять, що супротивне йому твердження - неправильне, і на цій підставі роблять висновок, що правильне доводжуване твердження.
+Метод математичної індукції. Логічною основою цього методу є принцип математичної індукції, взятий в шкільному курсі за аксіому: якщо твердження А(п), яке залежить від натурального числа п, виконується для п = 1 або п = щ та із припущення, що воно виконується для натурального числа п = k, де k > и0, випливає, що воно виконується і для п = k + 1, то це твердження виконується для будь-якого натурального числа п(п > п0).
+Векторний метод. Векторний метод доведення геометричних тверджень полягає в тому, що їхні умови і вимоги перекладають на мову векторів. Отримані векторні рівності приводять до потрібного вигляду на основі властивостей операцій над векторами, а потім результат перекладають у зворотному напрямі - на мову геометрії.
Дата добавления: 2019-02-12; просмотров: 889; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!