Основные характеристики звезд
 11.1 Из соотношения масса -- cветимость
11.1 Из соотношения масса -- cветимость 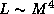 для
для 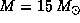 находим
находим 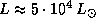 . Эффективная температура звезды главной последовательности спектрального класса B0 равна
. Эффективная температура звезды главной последовательности спектрального класса B0 равна 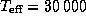 K. Радиус звезды найдем из соотношения между светимостью, радиусом и эффективной температурой
K. Радиус звезды найдем из соотношения между светимостью, радиусом и эффективной температурой

что дает
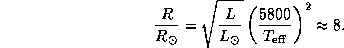
Поэтому
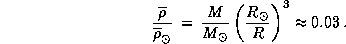
Средняя плотность Солнца 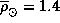 г/см3, так что
г/см3, так что 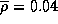 г/см3. Не правда ли, полученный результат противоречит тому, что подсказывает "здравый смысл" -- будто бы с ростом массы плотность должна расти. Так называемый "здравый смысл" имеет разумную область применимости -- свою у каждого, и подобные задачи помогут вам расширить ее.
г/см3. Не правда ли, полученный результат противоречит тому, что подсказывает "здравый смысл" -- будто бы с ростом массы плотность должна расти. Так называемый "здравый смысл" имеет разумную область применимости -- свою у каждого, и подобные задачи помогут вам расширить ее.
 11.2 Деля светимость Солнца на площадь его поверхности, получаем поток с 1 см2:
11.2 Деля светимость Солнца на площадь его поверхности, получаем поток с 1 см2:
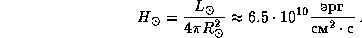
По определению, поток с единицы поверхности Солнца связан с его эффективной температурой следующим образом:

где 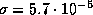 -- постоянная Стефана. Подставляя сюда найденное выше значение потока, получим для Солнца
-- постоянная Стефана. Подставляя сюда найденное выше значение потока, получим для Солнца

Поучительно перевести это число в нечто более ощутимое "для обывателя". Поток с поверхности Солнца соответствует тому, что с 1 см2 излучается 6.5 кВт (проверьте!).
 11.3 Мы имеем
11.3 Мы имеем

Найдем дифференциал логарифма L:
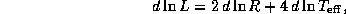
или
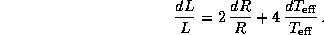
Для малых приращений радиуса и температуры последнее точное выражение можно заменить на приближенное
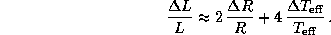
Подставляя сюда из условия задачи 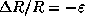 и
и 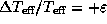 , приближенно имеем
, приближенно имеем 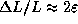 , так что при
, так что при 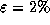 светимость звезды возрастет примерно на 4%.
светимость звезды возрастет примерно на 4%.
 11.4 При сравнении абсолютных звездных величин считается, что звезды находятся на одном и том же стандартном расстоянии (10 пк). В этом случае освещенности от разных звезд просто пропорциональны их светимостям. Тогда для нашей пары звезд имеем
11.4 При сравнении абсолютных звездных величин считается, что звезды находятся на одном и том же стандартном расстоянии (10 пк). В этом случае освещенности от разных звезд просто пропорциональны их светимостям. Тогда для нашей пары звезд имеем
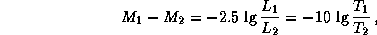
где мы воспользовались известным соотношением между светимостью, радиусом и эффективной температурой звезды (см. предыдущую задачу) и учли, что по условию 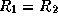 . Пусть первая звезда горячее (на 10%) второй, т.е.
. Пусть первая звезда горячее (на 10%) второй, т.е. 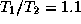 . Учитывая малое отличие отношения температур от единицы, приближенно находим
. Учитывая малое отличие отношения температур от единицы, приближенно находим
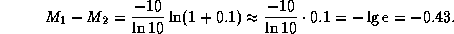
Тот факт, что 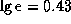 , следует помнить.
, следует помнить.
|
|
|
 11.5 Дифференцируя формулу, выражающую закон Стефана-Больцмана, легко получить, считая радиус постоянным (см., например, задачу
11.5 Дифференцируя формулу, выражающую закон Стефана-Больцмана, легко получить, считая радиус постоянным (см., например, задачу  )
)

Таким образом, чтобы светимости двух звезд одинакового радиуса отличались на 4%, их температуры должны разниться на 1%. Далее, по закону смещения Вина 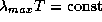 , и поэтому
, и поэтому 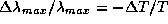 , так что при увеличении температуры на 1% длина волны максимума в распределении энергии уменьшается тоже на 1%. Сходным образом показывается, что интенсивность в максимуме при росте температуры на 1% увеличивается на 5%, а интенсивность в рэлей-джинсовской области -- на 1% (поймите, почему).
, так что при увеличении температуры на 1% длина волны максимума в распределении энергии уменьшается тоже на 1%. Сходным образом показывается, что интенсивность в максимуме при росте температуры на 1% увеличивается на 5%, а интенсивность в рэлей-джинсовской области -- на 1% (поймите, почему).
 11.6 Высота однородной атмосферы связана с температурой T, ускорением силы тяжести g и средней молярной массой
11.6 Высота однородной атмосферы связана с температурой T, ускорением силы тяжести g и средней молярной массой  следующим соотношением:
следующим соотношением:

где  г -- атомная единица массы. Для Солнца
г -- атомная единица массы. Для Солнца 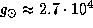 см/с2,
см/с2, 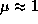 (атмосфера Солнца состоит в основном из водорода и он не ионизован), наконец,
(атмосфера Солнца состоит в основном из водорода и он не ионизован), наконец, 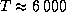 K, что в итоге дает
K, что в итоге дает 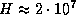 см, или около 200 км.
см, или около 200 км.
|
|
|
Ускорение силы тяжести на поверхности белого карлика можно выразить через его массу и радиус в солнечных единицах:
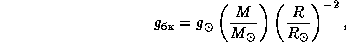
откуда находим для нашего белого карлика  см/с2. (Это колоссальное ускорение. Материальная точка, движущаяся с таким ускорением, за первую секунду проходит путь в 1500 км, что составляет около четверти радиуса белого карлика.) Учитывая также, что при
см/с2. (Это колоссальное ускорение. Материальная точка, движущаяся с таким ускорением, за первую секунду проходит путь в 1500 км, что составляет около четверти радиуса белого карлика.) Учитывая также, что при 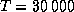 K водород ионизован, так что
K водород ионизован, так что 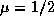 , для высоты однородной атмосферы белого карлика получаем
, для высоты однородной атмосферы белого карлика получаем
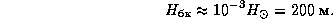
Уместно вспомнить, что для Земли, имеющей тот же приблизительно радиус, что и у белого карлика, высота однородной атмосферы составляет 8 км.
 11.7 Мы имеем
11.7 Мы имеем

где  -- постоянная Стефана. Если светимость и радиус выразить в солнечных единицах, то получим отсюда
-- постоянная Стефана. Если светимость и радиус выразить в солнечных единицах, то получим отсюда

где использовано значение эффективной температуры Солнца 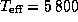 K. С помощью последней формулы находим, что светимость белого карлика в светимостях Солнца равна
K. С помощью последней формулы находим, что светимость белого карлика в светимостях Солнца равна
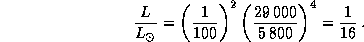
Множителю 16 отвечает разница почти точно в 3 звездные величины (это полезно помнить; вот более точное значение: 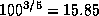 ). Поэтому абсолютная болометрическая звездная величина белого карлика будет на 3 звездные величины больше, чем у Солнца. Так чему же она равна?
). Поэтому абсолютная болометрическая звездная величина белого карлика будет на 3 звездные величины больше, чем у Солнца. Так чему же она равна?
|
|
|
 11.8 Из сравнения абсолютных звездных величин белого карлика и Солнца найдем отношение их светимостей:
11.8 Из сравнения абсолютных звездных величин белого карлика и Солнца найдем отношение их светимостей:
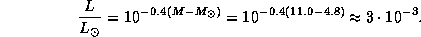
Далее, по формуле из решения предыдущей задачи оценим радиус белого карлика
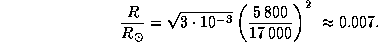
Это около 5000 км, т.е. меньше радиуса Земли (6400 км).
 11.9 Фотон с энергией
11.9 Фотон с энергией 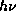 несет импульс
несет импульс 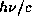 в направлении своего полета. После отражения от неподвижной или медленно удаляющейся от звезды фольги импульс фотона оказывается направлен в противоположную сторону, а его величина та же, что и до отражения. Поэтому при отражении каждого фотона фольге передается импульс
в направлении своего полета. После отражения от неподвижной или медленно удаляющейся от звезды фольги импульс фотона оказывается направлен в противоположную сторону, а его величина та же, что и до отражения. Поэтому при отражении каждого фотона фольге передается импульс 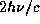 . Скорость передачи импульса есть сила светового давления на фольгу. В расчете на единицу площади она равна, таким образом,
. Скорость передачи импульса есть сила светового давления на фольгу. В расчете на единицу площади она равна, таким образом, 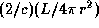 , где L -- светимость и r -- расстояние до звезды. Чтобы фольга с сидящим на ней комаром пренебрежимо малой массы улетела к другим звездам, световое давление должно превышать силу притяжения. В расчете на единицу площади поверхности фольги толщины H, изготовленной из материала с плотностью
, где L -- светимость и r -- расстояние до звезды. Чтобы фольга с сидящим на ней комаром пренебрежимо малой массы улетела к другим звездам, световое давление должно превышать силу притяжения. В расчете на единицу площади поверхности фольги толщины H, изготовленной из материала с плотностью  , сила притяжения составляет
, сила притяжения составляет 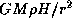 , где M -- масса звезды. Итак, чтобы фольга могла служить фотонным парусом, на котором можно улететь от звезды на бесконечность, должно выполняться условие
, где M -- масса звезды. Итак, чтобы фольга могла служить фотонным парусом, на котором можно улететь от звезды на бесконечность, должно выполняться условие

откуда

Здесь мы неявно предполагаем, что первоначально фольга покоится (а не движется вокруг звезды, скажем, по круговой орбите).
|
|
|
Обратите внимание, что r выпало. Причина, конечно, в том, что и сила притяжения, и поток зависят от r одинаково (как 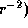 , так что если давление излучения превышает силу тяжести на каком-то расстоянии r, то оно превышает ее везде. Фольга металлическая, так что можно принять
, так что если давление излучения превышает силу тяжести на каком-то расстоянии r, то оно превышает ее везде. Фольга металлическая, так что можно принять 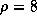 г/см3 (как у железа). Далее, для звезды класса O5V имеем
г/см3 (как у железа). Далее, для звезды класса O5V имеем 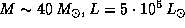 . Подставляя численные значения, находим, что H < 0.25 см. Как видим, в качестве "фольги" вполне сошел бы и покрашенный в белую краску лист кровельного железа!
. Подставляя численные значения, находим, что H < 0.25 см. Как видим, в качестве "фольги" вполне сошел бы и покрашенный в белую краску лист кровельного железа!
Возлежа вместо дивана на большом железном листе, от звезды класса O5 мог бы отправиться в межзвездное странствие не только комар, но и Обломов.
А теперь, пользуясь полученной формулой, немного пофантазируйте сами о межзвездных перелетах на фотонных парусах -- об их продолжительности, например. Что можно сказать о фотонных парусах для нашей Солнечной системы? Они даже были изготовлены, но из-за ограниченности финансирования космических программ до их реального использования дело пока не дошло.
Какова должна быть площадь невесомого фотонного паруса, на котором от Солнца к звездам могла бы улететь муха массой 1 г?
Физика звезд
 12.1 Энерговыделение происходит в объеме, и потому растет пропорционально кубу характерного размера объекта, теплоотвод же происходит с поверхности, а ее площадь возрастает как квадрат характерного размера. В итоге с увеличением размера тела (при сохранении темпа энерговыделения) его поверхностная температура должна расти. Дальше додумайте сами.
12.1 Энерговыделение происходит в объеме, и потому растет пропорционально кубу характерного размера объекта, теплоотвод же происходит с поверхности, а ее площадь возрастает как квадрат характерного размера. В итоге с увеличением размера тела (при сохранении темпа энерговыделения) его поверхностная температура должна расти. Дальше додумайте сами.
 12.2 Молярная масса газа -- это среднее значение массы одной частицы газа, выраженное в атомных единицах массы. Своим низким значением молярная масса солнечного вещества обязана, во-первых, тому, что основной его компонентой (70% по массе) является водород, и, во-вторых, практически полной его ионизации. При ионизации атома водорода, масса которого почти равна атомной единице массы, появляются две частицы -- протон и электрон. Масса электрона пренебрежимо мала по сравнению с массой протона. Поэтому молярная масса чисто водородного полностью ионизованного газа близка к 0.5. В недрах Солнца молярная масса немного больше этого значения (0.6). Причина -- присутствие более тяжелых элементов (молярная масса чисто гелиевого полностью ионизованного газа равна 4/3 [поймите, почему], для чистого кислорода она близка к 2 и т. д.).
12.2 Молярная масса газа -- это среднее значение массы одной частицы газа, выраженное в атомных единицах массы. Своим низким значением молярная масса солнечного вещества обязана, во-первых, тому, что основной его компонентой (70% по массе) является водород, и, во-вторых, практически полной его ионизации. При ионизации атома водорода, масса которого почти равна атомной единице массы, появляются две частицы -- протон и электрон. Масса электрона пренебрежимо мала по сравнению с массой протона. Поэтому молярная масса чисто водородного полностью ионизованного газа близка к 0.5. В недрах Солнца молярная масса немного больше этого значения (0.6). Причина -- присутствие более тяжелых элементов (молярная масса чисто гелиевого полностью ионизованного газа равна 4/3 [поймите, почему], для чистого кислорода она близка к 2 и т. д.).
Полное число частиц, составляющих Солнце, можно оценить следующим образом:
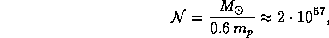
где  г -- атомная единица массы. Вклад в массу наружных неионизованных слоев, где значение
г -- атомная единица массы. Вклад в массу наружных неионизованных слоев, где значение  больше, пренебрежимо мал.
больше, пренебрежимо мал.
 12.3 При плотности в 150 г/см3 и средней молярной массе 0.6 (см. задачу
12.3 При плотности в 150 г/см3 и средней молярной массе 0.6 (см. задачу  ) концентрация частиц равна
) концентрация частиц равна
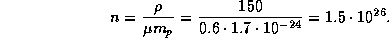
На самом деле средняя молярная масса в центре Солнца сейчас несколько больше, чем 0.6, так как водород там уже сильно выгорел, превратившись в гелий. Однако порядок величины n остается тем же, а только он нам и нужен.
Концентрация фотонов чернотельного излучения при температуре 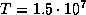 равна (см. задачу
равна (см. задачу  )
)

Это на три с лишним порядка меньше концентрации частиц. Значит, и роль давления излучения в недрах Солнца мала (см. решение задачи  ).
).
Любопытно, что, согласно расчетам моделей строения Солнца, в большей части его массы плотность  и температура T связаны соотношением
и температура T связаны соотношением 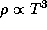 . Поэтому отношение
. Поэтому отношение 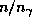 , найденное нами для центра Солнца, характерно для его недр в целом. Фотонов в недрах Солнца (и всех звезд, кроме самых массивных) гораздо меньше, чем протонов.
, найденное нами для центра Солнца, характерно для его недр в целом. Фотонов в недрах Солнца (и всех звезд, кроме самых массивных) гораздо меньше, чем протонов.
 12.4 Плотность воды 1 г/см3. При этом известно, что в жидкостях молекулы почти соприкасаются друг с другом. При плотностях, существенно больших плотности воды, имеющихся в недрах Солнца, атомы водорода ионизуются давлением. В результате доля объема, занятая частицами (соответственно атомами и голыми ядрами), уменьшается с
12.4 Плотность воды 1 г/см3. При этом известно, что в жидкостях молекулы почти соприкасаются друг с другом. При плотностях, существенно больших плотности воды, имеющихся в недрах Солнца, атомы водорода ионизуются давлением. В результате доля объема, занятая частицами (соответственно атомами и голыми ядрами), уменьшается с  до
до 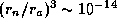 , где
, где 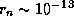 см -- размер ядра,
см -- размер ядра, 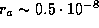 см -- размер атома. Таким образом, ядра начнут соприкасаться и "мешать" друг другу лишь при плотностях
см -- размер атома. Таким образом, ядра начнут соприкасаться и "мешать" друг другу лишь при плотностях 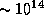 г/см3. Это -- ядерные плотности. Они характерны для нейтронных звезд. В принципе вплоть до этих плотностей ионизованное вещество может оставаться газом.
г/см3. Это -- ядерные плотности. Они характерны для нейтронных звезд. В принципе вплоть до этих плотностей ионизованное вещество может оставаться газом.
Наряду с плотностью, агрегатное состояние звездного вещества определяется температурой. Так, известно, что при понижении температуры белого карлика атомные ядра в его недрах должны выстраиваться в кристаллическую решетку. Чтобы ядра атомов двигались свободно, т.е. образовывали газ, требуется, чтобы их кинетическая энергия kT существенно превосходила энергию кулоновского взаимодействия, равную по порядку величины 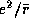 , где
, где 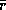 -- среднее расстояние между ядрами. Условие
-- среднее расстояние между ядрами. Условие 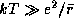 с использованием соотношений (для чисто водородной плазмы)
с использованием соотношений (для чисто водородной плазмы)
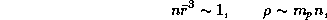
где n -- концентрация ядер, можно переписать в следующем виде:

или в числах

где 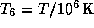 . Для центра Солнца имеем
. Для центра Солнца имеем 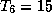 ,
, 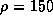 г/см3 (см. предыдущую задачу), так что
г/см3 (см. предыдущую задачу), так что 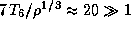 . Итак, даже при плотности в 150 г/см3 вещество в центре Солнца из-за высокой температуры остается газом.
. Итак, даже при плотности в 150 г/см3 вещество в центре Солнца из-за высокой температуры остается газом.
Дальнейшее придется принять на веру. Согласно расчетам моделей строения Солнца, соотношение 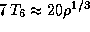 , справедливое для центра Солнца, приближенно выполняется и в большей части его недр. Поэтому повсюду в недрах Солнца, а не только в его центре, вещество является газом.
, справедливое для центра Солнца, приближенно выполняется и в большей части его недр. Поэтому повсюду в недрах Солнца, а не только в его центре, вещество является газом.
 12.5 Вычислим энергию, выделяющуюся при синтезе ядра атома гелия из четырех протонов. По формуле Эйнштейна
12.5 Вычислим энергию, выделяющуюся при синтезе ядра атома гелия из четырех протонов. По формуле Эйнштейна 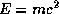 имеем
имеем 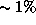 , так как в ходе данной ядерной реакции (точнее, цепочки реакций синтеза
, так как в ходе данной ядерной реакции (точнее, цепочки реакций синтеза  -частицы из четырех протонов) "исчезает"
-частицы из четырех протонов) "исчезает" 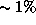 (точнее, 0.7%) массы. Полная энергия покоя Солнца равна
(точнее, 0.7%) массы. Полная энергия покоя Солнца равна 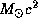 . Если бы Солнце целиком состояло из водорода, то при полном его превращении в гелий выделилась бы энергия
. Если бы Солнце целиком состояло из водорода, то при полном его превращении в гелий выделилась бы энергия 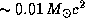 . Время, на которое этой энергии хватило бы для поддержания светимости Солнца на ее нынешнем уровне, составляет
. Время, на которое этой энергии хватило бы для поддержания светимости Солнца на ее нынешнем уровне, составляет  лет. Коэффициент 5/3 "несерьезен" -- Солнце не целиком состоит из водорода и т. д. В действительности за время своей жизни на главной последовательности Солнце успеет сжечь лишь примерно 10% своих запасов водорода. Таким образом, Солнцу отпущено примерно
лет. Коэффициент 5/3 "несерьезен" -- Солнце не целиком состоит из водорода и т. д. В действительности за время своей жизни на главной последовательности Солнце успеет сжечь лишь примерно 10% своих запасов водорода. Таким образом, Солнцу отпущено примерно 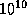 лет "спокойной" жизни на главной последовательности, что вовсе неплохо!
лет "спокойной" жизни на главной последовательности, что вовсе неплохо!
 12.6 Будем считать, что Солнце испускает чернотельное излучение с
12.6 Будем считать, что Солнце испускает чернотельное излучение с 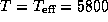 K. Средняя энергия, приходящаяся на один чернотельный фотон, равная
K. Средняя энергия, приходящаяся на один чернотельный фотон, равная 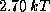 (см. задачу
(см. задачу  ), составляет тогда
), составляет тогда 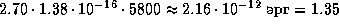 эВ. Поэтому число фотонов, излучаемых Солнцем за счет энергии, выделяющейся при синтезе одной
эВ. Поэтому число фотонов, излучаемых Солнцем за счет энергии, выделяющейся при синтезе одной  -частицы, равно
-частицы, равно 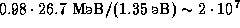 шт. Так как при синтезе
шт. Так как при синтезе  -частицы из четырех протонов два из них за счет
-частицы из четырех протонов два из них за счет 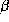 -распада превращаются в нейтроны, то при этом рождаются два нейтрино. В итоге число ежесекундно излучаемых Солнцем фотонов оказывается в
-распада превращаются в нейтроны, то при этом рождаются два нейтрино. В итоге число ежесекундно излучаемых Солнцем фотонов оказывается в 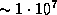 раз больше числа испускаемых им нейтрино.
раз больше числа испускаемых им нейтрино.
 12.7 Вещество, аккрецируемое Солнцем, при падении достигает у его поверхности второй космической скорости
12.7 Вещество, аккрецируемое Солнцем, при падении достигает у его поверхности второй космической скорости 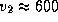 км/с. Искомый темп аккреции
км/с. Искомый темп аккреции  определим из условия равенства кинетической энергии выпадающего за 1 с вещества и светимости Солнца:
определим из условия равенства кинетической энергии выпадающего за 1 с вещества и светимости Солнца:

откуда

Как будет изменяться продолжительность года, т.е. период обращения Земли P при изменении массы Солнца? Из третьего закона Кеплера

находим

С другой стороны, должен сохраняться угловой момент 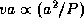 , так что
, так что

Из этих двух соотношений находим, что

откуда при 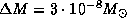 получаем, что
получаем, что 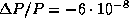 . Это соответствует уменьшению продолжительности года на
. Это соответствует уменьшению продолжительности года на 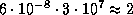 c в год, чего явно не происходит. Можно поэтому с уверенностью утверждать, что Солнце светит не за счет аккреции.
c в год, чего явно не происходит. Можно поэтому с уверенностью утверждать, что Солнце светит не за счет аккреции.
 12.8 По значениям температур можно заключить, что речь идет о массивных звездах, светимость которых обеспечивается CN-циклом. Известно, что темп энерговыделения при реакциях CN-цикла примерно пропорционален
12.8 По значениям температур можно заключить, что речь идет о массивных звездах, светимость которых обеспечивается CN-циклом. Известно, что темп энерговыделения при реакциях CN-цикла примерно пропорционален 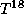 . Поэтому искомое отношение равно
. Поэтому искомое отношение равно 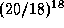 . Не хватайтесь за калькулятор -- все можно подсчитать в уме, воспользовавшись замечательным пределом
. Не хватайтесь за калькулятор -- все можно подсчитать в уме, воспользовавшись замечательным пределом

Действительно,
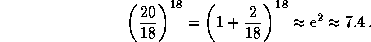
При росте температуры всего на 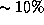 темп энерговыделения возрастает более чем в 7 раз!
темп энерговыделения возрастает более чем в 7 раз!
 12.9 Ответ очевиден: один год. При меньшем периоде центробежная сила разорвет звезду.
12.9 Ответ очевиден: один год. При меньшем периоде центробежная сила разорвет звезду.
 12.10 Приравнивая центробежную силу на экваторе пульсара
12.10 Приравнивая центробежную силу на экваторе пульсара 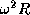 к силе тяжести
к силе тяжести  , получаем предельную угловую скорость вращения:
, получаем предельную угловую скорость вращения: 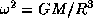 . Быстрее вращаться пульсар не может, так как тогда центробежная сила разорвет его. Предельный период вращения есть
. Быстрее вращаться пульсар не может, так как тогда центробежная сила разорвет его. Предельный период вращения есть 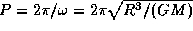 . Плотность звезды с таким периодом вращения равна
. Плотность звезды с таким периодом вращения равна
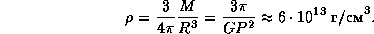
Это -- нижняя оценка плотности, при которой пульсар с периодом 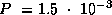 с не будет еще разорван центробежной силой. Мы получили разумную оценку плотности нейтронных звезд. Она близка к ядерной:
с не будет еще разорван центробежной силой. Мы получили разумную оценку плотности нейтронных звезд. Она близка к ядерной: 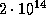 г/см3.
г/см3.
 12.11 Время схлопывания Солнца в точку -- это время свободного падения к центру Солнца тела, которое в начальный момент покоилось на его поверхности. Рассматривая движение такого тела, можно принять, что вся масса Солнца сосредоточена в центре (это допущение справедливо, если тело в процессе движения не обгоняет опадающие на центр слои, расположенные ниже; детальный анализ показывает, что это действительно так). Тогда время свободного падения равно половине периода P обращения тела по выродившейся в отрезок эллиптической орбите с большой полуосью
12.11 Время схлопывания Солнца в точку -- это время свободного падения к центру Солнца тела, которое в начальный момент покоилось на его поверхности. Рассматривая движение такого тела, можно принять, что вся масса Солнца сосредоточена в центре (это допущение справедливо, если тело в процессе движения не обгоняет опадающие на центр слои, расположенные ниже; детальный анализ показывает, что это действительно так). Тогда время свободного падения равно половине периода P обращения тела по выродившейся в отрезок эллиптической орбите с большой полуосью 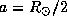 (и эксцентриситетом e=1). Этот период мы вычислим по третьему закону Кеплера (см. также задачи
(и эксцентриситетом e=1). Этот период мы вычислим по третьему закону Кеплера (см. также задачи  и
и  ):
):
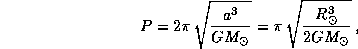
откуда для времени схлопывания Солнца 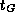 (индекс G -- от gravitation) находим
(индекс G -- от gravitation) находим
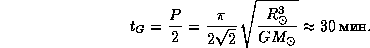
Это -- важное характерное время. При нарушениях механического равновесия заметные изменения должны происходить на временах 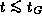 . Поскольку никаких существенных изменений в состоянии Солнца не происходит на гораздо больших временных интервалах -- это прямой наблюдательный факт, -- то можно с уверенностью утверждать, что Солнце находится в механическом (гидростатическом) равновесии.
. Поскольку никаких существенных изменений в состоянии Солнца не происходит на гораздо больших временных интервалах -- это прямой наблюдательный факт, -- то можно с уверенностью утверждать, что Солнце находится в механическом (гидростатическом) равновесии.
Использованные выше рассуждения дают следующее выражение для времени схлопывания произвольного сферически-симметричного самогравитирующего облака массы M, первоначально имевшего радиус R:

где  -- начальная средняя плотность облака. Подставив сюда
-- начальная средняя плотность облака. Подставив сюда 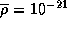 г/см3, найдем, что время схлопывания межзвездного облака такой начальной плотности составляет
г/см3, найдем, что время схлопывания межзвездного облака такой начальной плотности составляет 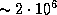 лет.
лет.
 12.12 Проведем анализ размерностей фигурирующих в задаче величин (ср. задачу
12.12 Проведем анализ размерностей фигурирующих в задаче величин (ср. задачу  ). У нас имеются следующие размерные параметры: масса "планеты" (или лучше сказать -- самогравитирующего тела) M, ее радиус R, размерная постоянная K, входящая в уравнение состояния
). У нас имеются следующие размерные параметры: масса "планеты" (или лучше сказать -- самогравитирующего тела) M, ее радиус R, размерная постоянная K, входящая в уравнение состояния 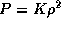 и, наконец, постоянная тяготения G. Пусть [Q] -- размерность величины Q. Тогда, с одной стороны,
и, наконец, постоянная тяготения G. Пусть [Q] -- размерность величины Q. Тогда, с одной стороны, 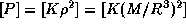 , с другой же стороны ньютонова сила тяготения
, с другой же стороны ньютонова сила тяготения 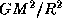 , отнесенная к площади поверхности сферы радиуса R, также имеет размерность давления:
, отнесенная к площади поверхности сферы радиуса R, также имеет размерность давления: 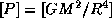 . Отношение двух фигурирующих здесь комбинаций определяющих размерных величин есть отвлеченное число. Обозначим его
. Отношение двух фигурирующих здесь комбинаций определяющих размерных величин есть отвлеченное число. Обозначим его 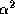 , так что
, так что
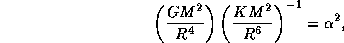
откуда

Следует ожидать, что  -- число порядка единицы: так "всегда" бывает.
-- число порядка единицы: так "всегда" бывает.
Из полученного сейчас выражения следует, что радиус самогравитирующей равновесной конфигурации, построенной из вещества с уравнением состояния 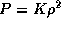 , однозначно определяется значением K. Замечательно, что масса M выпала. Отсюда можно заключить, что от добавления массы или от удаления с тела части его вещества радиус "планеты" меняться не будет. Оказывается поэтому, что если вещество имеет уравнение состояния
, однозначно определяется значением K. Замечательно, что масса M выпала. Отсюда можно заключить, что от добавления массы или от удаления с тела части его вещества радиус "планеты" меняться не будет. Оказывается поэтому, что если вещество имеет уравнение состояния 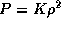 , то в один и тот же объем можно поместить любую массу. В действительности, конечно, масса все же будет ограничена сверху, так как при добавлении вещества гравитационная потенциальная яма будет становиться глубже. Скорость убегания
, то в один и тот же объем можно поместить любую массу. В действительности, конечно, масса все же будет ограничена сверху, так как при добавлении вещества гравитационная потенциальная яма будет становиться глубже. Скорость убегания

будет расти 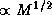 . Когда она станет приближаться к скорости света c, должны начать проявляться отклонения поля тяготения от ньютонова за счет эффектов общей теории относительности.
. Когда она станет приближаться к скорости света c, должны начать проявляться отклонения поля тяготения от ньютонова за счет эффектов общей теории относительности.
Полученный результат -- независимость R от M -- кажется настолько невероятным, что сначала верится в него с трудом. Подтвердим его более детальным анализом (менее подготовленные читатели могут его пропустить). Это позволит получить значение  . После этого поймем "на пальцах", в чем же суть дела, и обсудим некоторые важные для физики компактных звезд заключения общего характера, которые можно сделать на основе анализа нашей простой задачи.
. После этого поймем "на пальцах", в чем же суть дела, и обсудим некоторые важные для физики компактных звезд заключения общего характера, которые можно сделать на основе анализа нашей простой задачи.
Переходим к более аккуратному рассмотрению, которое позволит нам получить  . Уравнение механического равновесия самогравитирующей сферически-симметричной конфигурации (звезды, планеты) имет вид
. Уравнение механического равновесия самогравитирующей сферически-симметричной конфигурации (звезды, планеты) имет вид

При 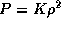 это дает
это дает

Здесь 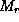 -- масса в сфере радиуса r, так что
-- масса в сфере радиуса r, так что

Поэтому из предыдущего уравнения следует, что
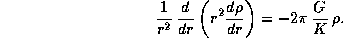
Если ввести

то это уравнение приводится к виду

где

Мы пришли к уравнению, по форме совпадающему с уравнением гармонических колебаний. (Для этого достаточно было догадаться ввести новую неизвестную y вместо  .) Общее его решение имеет вид
.) Общее его решение имеет вид
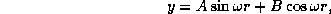
где A и B -- произвольные постоянные. При r=0 значение 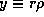 равно, очевидно, нулю, и поэтому B=0. Итак,
равно, очевидно, нулю, и поэтому B=0. Итак,
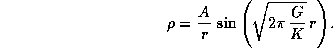
На поверхности тела, при r=R, мы должны иметь 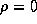 , откуда находим
, откуда находим

так что

Таким образом, аккуратный расчет полностью подтвердил то, что дал простой анализ размерностей. Безразмерный параметр  действительно оказался близок к единице:
действительно оказался близок к единице:

Если вдуматься, то неизменность радиуса при добавлении или удалении вещества не есть что-то невероятное. При добавлении массы, казалось бы, радиус будет возрастать. В этом "казалось бы" все и заключено. На самом деле добавляемое вещество имеет вес и потому сдавливает нижележащие слои. Если вещество несжимаемо, радиус тела растет 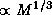 . На этом простейшем случае и основана "интуиция" тех, кто не учитывает влияния сжимаемости на изменение радиуса при росте массы.
. На этом простейшем случае и основана "интуиция" тех, кто не учитывает влияния сжимаемости на изменение радиуса при росте массы.
Если давление и плотность связаны степенной зависимостью

то говорят, что мы имеем дело с политропой индекса n. Рассматривавшийся нами случай соответствует n=1; при n=0 имеем несжимаемое вещество. Чем меньше n, тем труднее сжать вещество, тем оно "жестче". Теперь ясно, что при всех n<1 добавление массы сопровождается увеличением радиуса, в случае же n=1 нижние слои "проседают" под действием веса добавляемого вещества ровно на столько, что это компенсирует увеличение радиуса за счет добавления вещества. Если n>1, то с увеличением массы радиус должен убывать!
Бывает ли так? Да. Таковы, в частности, белые карлики. Чем больше масса белого карлика, тем меньше его радиус. При массах 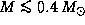 эта зависимость имеет вид
эта зависимость имеет вид 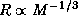 (что соответствует политропе индекса n=3/2), при больших массах, а потому и больших плотностях, поскольку радиус убывает с M, скорость убывания радиуса увеличивается. Объяснение того, почему это происходит, завело бы нас слишком далеко. Ограничимся констатацией этого факта. При приближении массы к так называемому пределу Чандрасекара
(что соответствует политропе индекса n=3/2), при больших массах, а потому и больших плотностях, поскольку радиус убывает с M, скорость убывания радиуса увеличивается. Объяснение того, почему это происходит, завело бы нас слишком далеко. Ограничимся констатацией этого факта. При приближении массы к так называемому пределу Чандрасекара 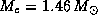 достигаются столь большие плотности, что вещество начинает радикально менять свои свойства: электроны начинают захватываться ядрами, превращая имеющиеся в них протоны в нейтроны. Идет процесс нейтронизации вещества. Белых карликов с массой, большей чандрасекаровского предела, в природе нет и быть не может -- зато могут быть и есть такие нейтронные звезды.
достигаются столь большие плотности, что вещество начинает радикально менять свои свойства: электроны начинают захватываться ядрами, превращая имеющиеся в них протоны в нейтроны. Идет процесс нейтронизации вещества. Белых карликов с массой, большей чандрасекаровского предела, в природе нет и быть не может -- зато могут быть и есть такие нейтронные звезды.
Физика звезд
 12.1 Энерговыделение происходит в объеме, и потому растет пропорционально кубу характерного размера объекта, теплоотвод же происходит с поверхности, а ее площадь возрастает как квадрат характерного размера. В итоге с увеличением размера тела (при сохранении темпа энерговыделения) его поверхностная температура должна расти. Дальше додумайте сами.
12.1 Энерговыделение происходит в объеме, и потому растет пропорционально кубу характерного размера объекта, теплоотвод же происходит с поверхности, а ее площадь возрастает как квадрат характерного размера. В итоге с увеличением размера тела (при сохранении темпа энерговыделения) его поверхностная температура должна расти. Дальше додумайте сами.
 12.2 Молярная масса газа -- это среднее значение массы одной частицы газа, выраженное в атомных единицах массы. Своим низким значением молярная масса солнечного вещества обязана, во-первых, тому, что основной его компонентой (70% по массе) является водород, и, во-вторых, практически полной его ионизации. При ионизации атома водорода, масса которого почти равна атомной единице массы, появляются две частицы -- протон и электрон. Масса электрона пренебрежимо мала по сравнению с массой протона. Поэтому молярная масса чисто водородного полностью ионизованного газа близка к 0.5. В недрах Солнца молярная масса немного больше этого значения (0.6). Причина -- присутствие более тяжелых элементов (молярная масса чисто гелиевого полностью ионизованного газа равна 4/3 [поймите, почему], для чистого кислорода она близка к 2 и т. д.).
12.2 Молярная масса газа -- это среднее значение массы одной частицы газа, выраженное в атомных единицах массы. Своим низким значением молярная масса солнечного вещества обязана, во-первых, тому, что основной его компонентой (70% по массе) является водород, и, во-вторых, практически полной его ионизации. При ионизации атома водорода, масса которого почти равна атомной единице массы, появляются две частицы -- протон и электрон. Масса электрона пренебрежимо мала по сравнению с массой протона. Поэтому молярная масса чисто водородного полностью ионизованного газа близка к 0.5. В недрах Солнца молярная масса немного больше этого значения (0.6). Причина -- присутствие более тяжелых элементов (молярная масса чисто гелиевого полностью ионизованного газа равна 4/3 [поймите, почему], для чистого кислорода она близка к 2 и т. д.).
Полное число частиц, составляющих Солнце, можно оценить следующим образом:
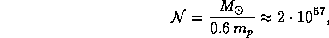
где  г -- атомная единица массы. Вклад в массу наружных неионизованных слоев, где значение
г -- атомная единица массы. Вклад в массу наружных неионизованных слоев, где значение  больше, пренебрежимо мал.
больше, пренебрежимо мал.
 12.3 При плотности в 150 г/см3 и средней молярной массе 0.6 (см. задачу
12.3 При плотности в 150 г/см3 и средней молярной массе 0.6 (см. задачу  ) концентрация частиц равна
) концентрация частиц равна
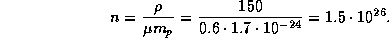
На самом деле средняя молярная масса в центре Солнца сейчас несколько больше, чем 0.6, так как водород там уже сильно выгорел, превратившись в гелий. Однако порядок величины n остается тем же, а только он нам и нужен.
Концентрация фотонов чернотельного излучения при температуре 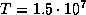 равна (см. задачу
равна (см. задачу  )
)

Это на три с лишним порядка меньше концентрации частиц. Значит, и роль давления излучения в недрах Солнца мала (см. решение задачи  ).
).
Любопытно, что, согласно расчетам моделей строения Солнца, в большей части его массы плотность  и температура T связаны соотношением
и температура T связаны соотношением 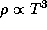 . Поэтому отношение
. Поэтому отношение 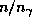 , найденное нами для центра Солнца, характерно для его недр в целом. Фотонов в недрах Солнца (и всех звезд, кроме самых массивных) гораздо меньше, чем протонов.
, найденное нами для центра Солнца, характерно для его недр в целом. Фотонов в недрах Солнца (и всех звезд, кроме самых массивных) гораздо меньше, чем протонов.
 12.4 Плотность воды 1 г/см3. При этом известно, что в жидкостях молекулы почти соприкасаются друг с другом. При плотностях, существенно больших плотности воды, имеющихся в недрах Солнца, атомы водорода ионизуются давлением. В результате доля объема, занятая частицами (соответственно атомами и голыми ядрами), уменьшается с
12.4 Плотность воды 1 г/см3. При этом известно, что в жидкостях молекулы почти соприкасаются друг с другом. При плотностях, существенно больших плотности воды, имеющихся в недрах Солнца, атомы водорода ионизуются давлением. В результате доля объема, занятая частицами (соответственно атомами и голыми ядрами), уменьшается с  до
до 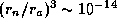 , где
, где 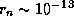 см -- размер ядра,
см -- размер ядра, 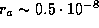 см -- размер атома. Таким образом, ядра начнут соприкасаться и "мешать" друг другу лишь при плотностях
см -- размер атома. Таким образом, ядра начнут соприкасаться и "мешать" друг другу лишь при плотностях 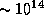 г/см3. Это -- ядерные плотности. Они характерны для нейтронных звезд. В принципе вплоть до этих плотностей ионизованное вещество может оставаться газом.
г/см3. Это -- ядерные плотности. Они характерны для нейтронных звезд. В принципе вплоть до этих плотностей ионизованное вещество может оставаться газом.
Наряду с плотностью, агрегатное состояние звездного вещества определяется температурой. Так, известно, что при понижении температуры белого карлика атомные ядра в его недрах должны выстраиваться в кристаллическую решетку. Чтобы ядра атомов двигались свободно, т.е. образовывали газ, требуется, чтобы их кинетическая энергия kT существенно превосходила энергию кулоновского взаимодействия, равную по порядку величины 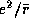 , где
, где 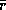 -- среднее расстояние между ядрами. Условие
-- среднее расстояние между ядрами. Условие 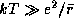 с использованием соотношений (для чисто водородной плазмы)
с использованием соотношений (для чисто водородной плазмы)
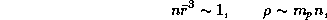
где n -- концентрация ядер, можно переписать в следующем виде:

или в числах

где 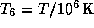 . Для центра Солнца имеем
. Для центра Солнца имеем 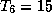 ,
, 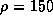 г/см3 (см. предыдущую задачу), так что
г/см3 (см. предыдущую задачу), так что 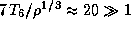 . Итак, даже при плотности в 150 г/см3 вещество в центре Солнца из-за высокой температуры остается газом.
. Итак, даже при плотности в 150 г/см3 вещество в центре Солнца из-за высокой температуры остается газом.
Дальнейшее придется принять на веру. Согласно расчетам моделей строения Солнца, соотношение 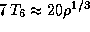 , справедливое для центра Солнца, приближенно выполняется и в большей части его недр. Поэтому повсюду в недрах Солнца, а не только в его центре, вещество является газом.
, справедливое для центра Солнца, приближенно выполняется и в большей части его недр. Поэтому повсюду в недрах Солнца, а не только в его центре, вещество является газом.
 12.5 Вычислим энергию, выделяющуюся при синтезе ядра атома гелия из четырех протонов. По формуле Эйнштейна
12.5 Вычислим энергию, выделяющуюся при синтезе ядра атома гелия из четырех протонов. По формуле Эйнштейна 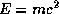 имеем
имеем 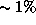 , так как в ходе данной ядерной реакции (точнее, цепочки реакций синтеза
, так как в ходе данной ядерной реакции (точнее, цепочки реакций синтеза  -частицы из четырех протонов) "исчезает"
-частицы из четырех протонов) "исчезает" 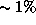 (точнее, 0.7%) массы. Полная энергия покоя Солнца равна
(точнее, 0.7%) массы. Полная энергия покоя Солнца равна 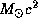 . Если бы Солнце целиком состояло из водорода, то при полном его превращении в гелий выделилась бы энергия
. Если бы Солнце целиком состояло из водорода, то при полном его превращении в гелий выделилась бы энергия 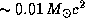 . Время, на которое этой энергии хватило бы для поддержания светимости Солнца на ее нынешнем уровне, составляет
. Время, на которое этой энергии хватило бы для поддержания светимости Солнца на ее нынешнем уровне, составляет  лет. Коэффициент 5/3 "несерьезен" -- Солнце не целиком состоит из водорода и т. д. В действительности за время своей жизни на главной последовательности Солнце успеет сжечь лишь примерно 10% своих запасов водорода. Таким образом, Солнцу отпущено примерно
лет. Коэффициент 5/3 "несерьезен" -- Солнце не целиком состоит из водорода и т. д. В действительности за время своей жизни на главной последовательности Солнце успеет сжечь лишь примерно 10% своих запасов водорода. Таким образом, Солнцу отпущено примерно 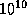 лет "спокойной" жизни на главной последовательности, что вовсе неплохо!
лет "спокойной" жизни на главной последовательности, что вовсе неплохо!
 12.6 Будем считать, что Солнце испускает чернотельное излучение с
12.6 Будем считать, что Солнце испускает чернотельное излучение с 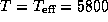 K. Средняя энергия, приходящаяся на один чернотельный фотон, равная
K. Средняя энергия, приходящаяся на один чернотельный фотон, равная 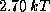 (см. задачу
(см. задачу  ), составляет тогда
), составляет тогда 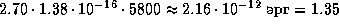 эВ. Поэтому число фотонов, излучаемых Солнцем за счет энергии, выделяющейся при синтезе одной
эВ. Поэтому число фотонов, излучаемых Солнцем за счет энергии, выделяющейся при синтезе одной  -частицы, равно
-частицы, равно 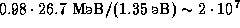 шт. Так как при синтезе
шт. Так как при синтезе  -частицы из четырех протонов два из них за счет
-частицы из четырех протонов два из них за счет 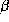 -распада превращаются в нейтроны, то при этом рождаются два нейтрино. В итоге число ежесекундно излучаемых Солнцем фотонов оказывается в
-распада превращаются в нейтроны, то при этом рождаются два нейтрино. В итоге число ежесекундно излучаемых Солнцем фотонов оказывается в 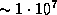 раз больше числа испускаемых им нейтрино.
раз больше числа испускаемых им нейтрино.
 12.7 Вещество, аккрецируемое Солнцем, при падении достигает у его поверхности второй космической скорости
12.7 Вещество, аккрецируемое Солнцем, при падении достигает у его поверхности второй космической скорости 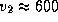 км/с. Искомый темп аккреции
км/с. Искомый темп аккреции  определим из условия равенства кинетической энергии выпадающего за 1 с вещества и светимости Солнца:
определим из условия равенства кинетической энергии выпадающего за 1 с вещества и светимости Солнца:

откуда

Как будет изменяться продолжительность года, т.е. период обращения Земли P при изменении массы Солнца? Из третьего закона Кеплера

находим

С другой стороны, должен сохраняться угловой момент 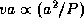 , так что
, так что

Из этих двух соотношений находим, что

откуда при 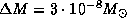 получаем, что
получаем, что 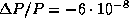 . Это соответствует уменьшению продолжительности года на
. Это соответствует уменьшению продолжительности года на 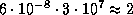 c в год, чего явно не происходит. Можно поэтому с уверенностью утверждать, что Солнце светит не за счет аккреции.
c в год, чего явно не происходит. Можно поэтому с уверенностью утверждать, что Солнце светит не за счет аккреции.
 12.8 По значениям температур можно заключить, что речь идет о массивных звездах, светимость которых обеспечивается CN-циклом. Известно, что темп энерговыделения при реакциях CN-цикла примерно пропорционален
12.8 По значениям температур можно заключить, что речь идет о массивных звездах, светимость которых обеспечивается CN-циклом. Известно, что темп энерговыделения при реакциях CN-цикла примерно пропорционален 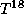 . Поэтому искомое отношение равно
. Поэтому искомое отношение равно 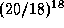 . Не хватайтесь за калькулятор -- все можно подсчитать в уме, воспользовавшись замечательным пределом
. Не хватайтесь за калькулятор -- все можно подсчитать в уме, воспользовавшись замечательным пределом

Действительно,
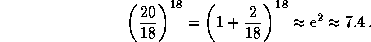
При росте температуры всего на 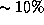 темп энерговыделения возрастает более чем в 7 раз!
темп энерговыделения возрастает более чем в 7 раз!
 12.9 Ответ очевиден: один год. При меньшем периоде центробежная сила разорвет звезду.
12.9 Ответ очевиден: один год. При меньшем периоде центробежная сила разорвет звезду.
 12.10 Приравнивая центробежную силу на экваторе пульсара
12.10 Приравнивая центробежную силу на экваторе пульсара 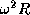 к силе тяжести
к силе тяжести  , получаем предельную угловую скорость вращения:
, получаем предельную угловую скорость вращения: 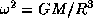 . Быстрее вращаться пульсар не может, так как тогда центробежная сила разорвет его. Предельный период вращения есть
. Быстрее вращаться пульсар не может, так как тогда центробежная сила разорвет его. Предельный период вращения есть 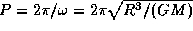 . Плотность звезды с таким периодом вращения равна
. Плотность звезды с таким периодом вращения равна
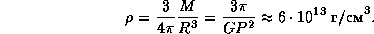
Это -- нижняя оценка плотности, при которой пульсар с периодом 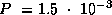 с не будет еще разорван центробежной силой. Мы получили разумную оценку плотности нейтронных звезд. Она близка к ядерной:
с не будет еще разорван центробежной силой. Мы получили разумную оценку плотности нейтронных звезд. Она близка к ядерной: 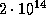 г/см3.
г/см3.
 12.11 Время схлопывания Солнца в точку -- это время свободного падения к центру Солнца тела, которое в начальный момент покоилось на его поверхности. Рассматривая движение такого тела, можно принять, что вся масса Солнца сосредоточена в центре (это допущение справедливо, если тело в процессе движения не обгоняет опадающие на центр слои, расположенные ниже; детальный анализ показывает, что это действительно так). Тогда время свободного падения равно половине периода P обращения тела по выродившейся в отрезок эллиптической орбите с большой полуосью
12.11 Время схлопывания Солнца в точку -- это время свободного падения к центру Солнца тела, которое в начальный момент покоилось на его поверхности. Рассматривая движение такого тела, можно принять, что вся масса Солнца сосредоточена в центре (это допущение справедливо, если тело в процессе движения не обгоняет опадающие на центр слои, расположенные ниже; детальный анализ показывает, что это действительно так). Тогда время свободного падения равно половине периода P обращения тела по выродившейся в отрезок эллиптической орбите с большой полуосью 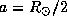 (и эксцентриситетом e=1). Этот период мы вычислим по третьему закону Кеплера (см. также задачи
(и эксцентриситетом e=1). Этот период мы вычислим по третьему закону Кеплера (см. также задачи  и
и  ):
):
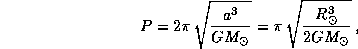
откуда для времени схлопывания Солнца 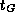 (индекс G -- от gravitation) находим
(индекс G -- от gravitation) находим
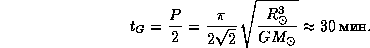
Это -- важное характерное время. При нарушениях механического равновесия заметные изменения должны происходить на временах 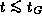 . Поскольку никаких существенных изменений в состоянии Солнца не происходит на гораздо больших временных интервалах -- это прямой наблюдательный факт, -- то можно с уверенностью утверждать, что Солнце находится в механическом (гидростатическом) равновесии.
. Поскольку никаких существенных изменений в состоянии Солнца не происходит на гораздо больших временных интервалах -- это прямой наблюдательный факт, -- то можно с уверенностью утверждать, что Солнце находится в механическом (гидростатическом) равновесии.
Использованные выше рассуждения дают следующее выражение для времени схлопывания произвольного сферически-симметричного самогравитирующего облака массы M, первоначально имевшего радиус R:

где  -- начальная средняя плотность облака. Подставив сюда
-- начальная средняя плотность облака. Подставив сюда 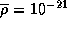 г/см3, найдем, что время схлопывания межзвездного облака такой начальной плотности составляет
г/см3, найдем, что время схлопывания межзвездного облака такой начальной плотности составляет 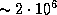 лет.
лет.
 12.12 Проведем анализ размерностей фигурирующих в задаче величин (ср. задачу
12.12 Проведем анализ размерностей фигурирующих в задаче величин (ср. задачу  ). У нас имеются следующие размерные параметры: масса "планеты" (или лучше сказать -- самогравитирующего тела) M, ее радиус R, размерная постоянная K, входящая в уравнение состояния
). У нас имеются следующие размерные параметры: масса "планеты" (или лучше сказать -- самогравитирующего тела) M, ее радиус R, размерная постоянная K, входящая в уравнение состояния 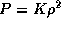 и, наконец, постоянная тяготения G. Пусть [Q] -- размерность величины Q. Тогда, с одной стороны,
и, наконец, постоянная тяготения G. Пусть [Q] -- размерность величины Q. Тогда, с одной стороны, 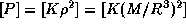 , с другой же стороны ньютонова сила тяготения
, с другой же стороны ньютонова сила тяготения 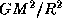 , отнесенная к площади поверхности сферы радиуса R, также имеет размерность давления:
, отнесенная к площади поверхности сферы радиуса R, также имеет размерность давления: 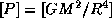 . Отношение двух фигурирующих здесь комбинаций определяющих размерных величин есть отвлеченное число. Обозначим его
. Отношение двух фигурирующих здесь комбинаций определяющих размерных величин есть отвлеченное число. Обозначим его 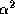 , так что
, так что
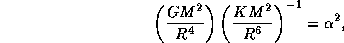
откуда

Следует ожидать, что  -- число порядка единицы: так "всегда" бывает.
-- число порядка единицы: так "всегда" бывает.
Из полученного сейчас выражения следует, что радиус самогравитирующей равновесной конфигурации, построенной из вещества с уравнением состояния 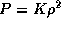 , однозначно определяется значением K. Замечательно, что масса M выпала. Отсюда можно заключить, что от добавления массы или от удаления с тела части его вещества радиус "планеты" меняться не будет. Оказывается поэтому, что если вещество имеет уравнение состояния
, однозначно определяется значением K. Замечательно, что масса M выпала. Отсюда можно заключить, что от добавления массы или от удаления с тела части его вещества радиус "планеты" меняться не будет. Оказывается поэтому, что если вещество имеет уравнение состояния 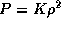 , то в один и тот же объем можно поместить любую массу. В действительности, конечно, масса все же будет ограничена сверху, так как при добавлении вещества гравитационная потенциальная яма будет становиться глубже. Скорость убегания
, то в один и тот же объем можно поместить любую массу. В действительности, конечно, масса все же будет ограничена сверху, так как при добавлении вещества гравитационная потенциальная яма будет становиться глубже. Скорость убегания

будет расти 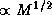 . Когда она станет приближаться к скорости света c, должны начать проявляться отклонения поля тяготения от ньютонова за счет эффектов общей теории относительности.
. Когда она станет приближаться к скорости света c, должны начать проявляться отклонения поля тяготения от ньютонова за счет эффектов общей теории относительности.
Полученный результат -- независимость R от M -- кажется настолько невероятным, что сначала верится в него с трудом. Подтвердим его более детальным анализом (менее подготовленные читатели могут его пропустить). Это позволит получить значение  . После этого поймем "на пальцах", в чем же суть дела, и обсудим некоторые важные для физики компактных звезд заключения общего характера, которые можно сделать на основе анализа нашей простой задачи.
. После этого поймем "на пальцах", в чем же суть дела, и обсудим некоторые важные для физики компактных звезд заключения общего характера, которые можно сделать на основе анализа нашей простой задачи.
Переходим к более аккуратному рассмотрению, которое позволит нам получить  . Уравнение механического равновесия самогравитирующей сферически-симметричной конфигурации (звезды, планеты) имет вид
. Уравнение механического равновесия самогравитирующей сферически-симметричной конфигурации (звезды, планеты) имет вид

При 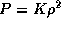 это дает
это дает

Здесь 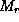 -- масса в сфере радиуса r, так что
-- масса в сфере радиуса r, так что

Поэтому из предыдущего уравнения следует, что
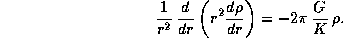
Если ввести

то это уравнение приводится к виду

где

Мы пришли к уравнению, по форме совпадающему с уравнением гармонических колебаний. (Для этого достаточно было догадаться ввести новую неизвестную y вместо  .) Общее его решение имеет вид
.) Общее его решение имеет вид
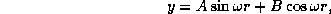
где A и B -- произвольные постоянные. При r=0 значение 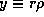 равно, очевидно, нулю, и поэтому B=0. Итак,
равно, очевидно, нулю, и поэтому B=0. Итак,
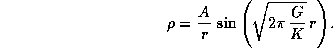
На поверхности тела, при r=R, мы должны иметь 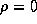 , откуда находим
, откуда находим

так что

Таким образом, аккуратный расчет полностью подтвердил то, что дал простой анализ размерностей. Безразмерный параметр  действительно оказался близок к единице:
действительно оказался близок к единице:

Если вдуматься, то неизменность радиуса при добавлении или удалении вещества не есть что-то невероятное. При добавлении массы, казалось бы, радиус будет возрастать. В этом "казалось бы" все и заключено. На самом деле добавляемое вещество имеет вес и потому сдавливает нижележащие слои. Если вещество несжимаемо, радиус тела растет 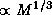 . На этом простейшем случае и основана "интуиция" тех, кто не учитывает влияния сжимаемости на изменение радиуса при росте массы.
. На этом простейшем случае и основана "интуиция" тех, кто не учитывает влияния сжимаемости на изменение радиуса при росте массы.
Если давление и плотность связаны степенной зависимостью

то говорят, что мы имеем дело с политропой индекса n. Рассматривавшийся нами случай соответствует n=1; при n=0 имеем несжимаемое вещество. Чем меньше n, тем труднее сжать вещество, тем оно "жестче". Теперь ясно, что при всех n<1 добавление массы сопровождается увеличением радиуса, в случае же n=1 нижние слои "проседают" под действием веса добавляемого вещества ровно на столько, что это компенсирует увеличение радиуса за счет добавления вещества. Если n>1, то с увеличением массы радиус должен убывать!
Бывает ли так? Да. Таковы, в частности, белые карлики. Чем больше масса белого карлика, тем меньше его радиус. При массах 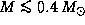 эта зависимость имеет вид
эта зависимость имеет вид 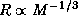 (что соответствует политропе индекса n=3/2), при больших массах, а потому и больших плотностях, поскольку радиус убывает с M, скорость убывания радиуса увеличивается. Объяснение того, почему это происходит, завело бы нас слишком далеко. Ограничимся констатацией этого факта. При приближении массы к так называемому пределу Чандрасекара
(что соответствует политропе индекса n=3/2), при больших массах, а потому и больших плотностях, поскольку радиус убывает с M, скорость убывания радиуса увеличивается. Объяснение того, почему это происходит, завело бы нас слишком далеко. Ограничимся констатацией этого факта. При приближении массы к так называемому пределу Чандрасекара 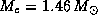 достигаются столь большие плотности, что вещество начинает радикально менять свои свойства: электроны начинают захватываться ядрами, превращая имеющиеся в них протоны в нейтроны. Идет процесс нейтронизации вещества. Белых карликов с массой, большей чандрасекаровского предела, в природе нет и быть не может -- зато могут быть и есть такие нейтронные звезды.
достигаются столь большие плотности, что вещество начинает радикально менять свои свойства: электроны начинают захватываться ядрами, превращая имеющиеся в них протоны в нейтроны. Идет процесс нейтронизации вещества. Белых карликов с массой, большей чандрасекаровского предела, в природе нет и быть не может -- зато могут быть и есть такие нейтронные звезды.
Двойные и переменные звезды
 13.1 Первая величина есть лучевая скорость центра масс двойной.
13.1 Первая величина есть лучевая скорость центра масс двойной.
Вычислим второй интеграл. Если центр масс двойной покоится, то для лучевой скорости нетрудно получить формулу 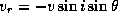 , где v -- орбитальная скорость, i -- угол между лучом зрения и нормалью к орбите, а
, где v -- орбитальная скорость, i -- угол между лучом зрения и нормалью к орбите, а 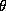 -- полярный угол в плоскости орбиты, за один оборот пробегающий значения от 0 до
-- полярный угол в плоскости орбиты, за один оборот пробегающий значения от 0 до  , так что
, так что 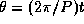 . Имеем
. Имеем
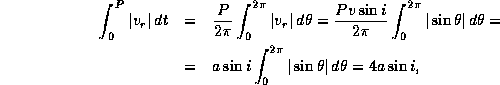
где a -- радиус орбиты.
 13.2 По периоду изменения блеска
13.2 По периоду изменения блеска 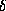 Cep оценим ее среднюю абсолютную звездную величину:
Cep оценим ее среднюю абсолютную звездную величину: 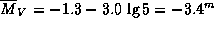 . На первый взгляд, приведенных в условии задачи данных недостаточно для ее решения -- нужно знать среднюю видимую звездную величину
. На первый взгляд, приведенных в условии задачи данных недостаточно для ее решения -- нужно знать среднюю видимую звездную величину 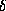 Cep, которая нам неизвестна. Однако неявно эта информация есть:
Cep, которая нам неизвестна. Однако неявно эта информация есть:  Cep, как показывает ее название, является четвертой по яркости звездой в созвездии Цефея. Но Цефей -- созвездие не из ярких, его звезды значительно, на полторы -- две звездных величины слабее звезд ковша Большой Медведицы. Поэтому в качестве разумной оценки среднего значения блеска
Cep, как показывает ее название, является четвертой по яркости звездой в созвездии Цефея. Но Цефей -- созвездие не из ярких, его звезды значительно, на полторы -- две звездных величины слабее звезд ковша Большой Медведицы. Поэтому в качестве разумной оценки среднего значения блеска  Cep можно принять 4
Cep можно принять 4  . Теперь по известной формуле
. Теперь по известной формуле
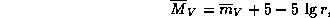
где r -- в парсеках, находим 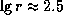 , откуда
, откуда 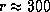 пк.
пк.
Несмотря на столь значительное расстояние,  Cep прекрасно видна простым глазом. Это сверхгигант. Cветимость
Cep прекрасно видна простым глазом. Это сверхгигант. Cветимость  Cep, как и всех цефеид, очень высока. Ведь иначе цефеиды не могли бы служить "маяками Вселенной"!
Cep, как и всех цефеид, очень высока. Ведь иначе цефеиды не могли бы служить "маяками Вселенной"!
 13.3 Естественно предположить, что частота колебаний блеска цефеиды
13.3 Естественно предположить, что частота колебаний блеска цефеиды 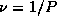 меняется с годовым периодом за счет эффекта Доплера, обусловленного орбитальным движением Земли. Мы имеем:
меняется с годовым периодом за счет эффекта Доплера, обусловленного орбитальным движением Земли. Мы имеем:

где 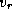 -- максимальная величина проекции вектора орбитальной скорости Земли
-- максимальная величина проекции вектора орбитальной скорости Земли  на прямую Солнце -- цефеида. Отсюда
на прямую Солнце -- цефеида. Отсюда
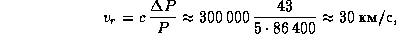
что совпадает с орбитальной скоростью Земли. Заключаем, что звезда лежит в плоскости эклиптики.
Период максимален, когда направление на звезду противоположно направлению движения Земли. Но, как легко сообразить (сделайте соответствующий чертеж), в конце декабря (зимнее солнцестояние) вектор скорости Земли направлен в точку осеннего равноденствия. Поэтому звезда находится на небе неподалеку от точки весеннего равноденствия, и ее экваториальные координаты 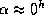 ,
, 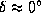 .
.
 13.4 По определению болометрической звездной величины имеем
13.4 По определению болометрической звездной величины имеем
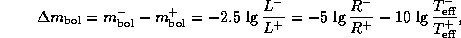
где 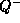 и
и 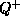 -- значения величины Q в минимуме и в максимуме блеска, соответственно. Изменения радиуса и блеска происходят, грубо говоря, в противофазе, так что в максимуме блеска радиус минимален. Положим поэтому
-- значения величины Q в минимуме и в максимуме блеска, соответственно. Изменения радиуса и блеска происходят, грубо говоря, в противофазе, так что в максимуме блеска радиус минимален. Положим поэтому
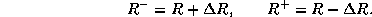
Подставляя значения
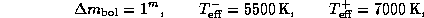
для относительного изменения радиуса цефеиды в ходе пульсаций находим
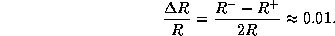
В действительности изменения блеска и радиуса у цефеид происходят не точно в противофазе -- имеется фазовое запаздывание, которым мы пренебрегли. Однако полученная оценка 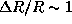 % близка к реальному изменению радиуса. Как видим, цефеиды совершают малые колебания.
% близка к реальному изменению радиуса. Как видим, цефеиды совершают малые колебания.
Главная мораль этой задачи: расхожее представление, будто основной причиной колебаний блеска цефеид является изменение их размеров в ходе пульсаций, ошибочно. Главный вклад в колебания блеска дают вариации температуры, а не радиуса!
 13.5 Из третьего закона Кеплера находим большую полуось орбиты двойной системы
13.5 Из третьего закона Кеплера находим большую полуось орбиты двойной системы

Здесь P выражено в годах, а массы -- в массах Солнца. Далее, расстояние от пульсара до центра масс системы равно
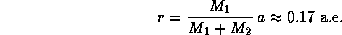
Зная r и P, можем оценить скорость орбитального движения пульсара: 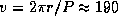 км/с. Из-за эффекта Доплера период пульсаций (обратный частоте) изменяется, причем амплитуда относительного изменения периода равна
км/с. Из-за эффекта Доплера период пульсаций (обратный частоте) изменяется, причем амплитуда относительного изменения периода равна
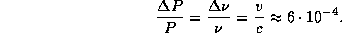
На самом деле эффект наблюдается как запаздывание (или опережение) времени прихода импульсов. Оно весьма значительно. Путь в 2r=0.34 а.е. излучение пульсара проходит за 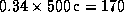 с. Это и есть максимальное запаздывание (опережение). Полное число импульсов, которое испускает наш пульсар за такое время, составляет 1700. Это есть недостача (или избыток) числа импульсов при перемещении пульсара от самой дальней от наблюдателя точки орбиты до самой ближней (или наоборот). За полупериод, т.е. за
с. Это и есть максимальное запаздывание (опережение). Полное число импульсов, которое испускает наш пульсар за такое время, составляет 1700. Это есть недостача (или избыток) числа импульсов при перемещении пульсара от самой дальней от наблюдателя точки орбиты до самой ближней (или наоборот). За полупериод, т.е. за 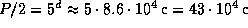 пульсар испускает
пульсар испускает 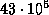 импульсов. Среднее за полупериод запаздывание (или опережение) составляет, таким образом,
импульсов. Среднее за полупериод запаздывание (или опережение) составляет, таким образом, 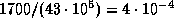 . Ясно, что так как период пульсаций меняется синусоидально, то для получения максимальной величины надо это число поделить на среднее от одной полуволны синусоиды
. Ясно, что так как период пульсаций меняется синусоидально, то для получения максимальной величины надо это число поделить на среднее от одной полуволны синусоиды

В результате получаем то же число ( 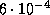 ), которое было найдено выше другим путем.
), которое было найдено выше другим путем.
По сути дела, описанное запаздывание времен прихода импульсов у рентгеновских пульсаров -- это тот же эффект, по которому Ремер в 17 веке впервые измерил скорость света. В его распоряжении была эфемерида, рассчитанная по наблюдениям затмений Ио в период, когда Юпитер был в противостоянии, и наблюдения затмений Ио Юпитером, находящимся в соединении с Солнцем. Эти наблюдения показывали, что затмения спутника запаздывают по сравнению с эфемеридой. Ремер правильно объяснил запаздывание конечностью скорости распространения света и получил правильную по порядку величины оценку этой скорости.
 13.6 В задаче
13.6 В задаче  мы оценили угол, под которым с
мы оценили угол, под которым с  Cen видна большая полуось орбиты Юпитера, и нашли, что он равен примерно
Cen видна большая полуось орбиты Юпитера, и нашли, что он равен примерно  . Оценим теперь видимую звездную величину Юпитера для наблюдателя на
. Оценим теперь видимую звездную величину Юпитера для наблюдателя на  Cen. Радиус Юпитера составляет примерно
Cen. Радиус Юпитера составляет примерно 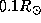 (его нет во "Вселенной в числах", но его легко можно вычислить по имеющимся там данным о массе и средней плотности Юпитера). Видимую звездную величину Юпитера для наблюдателя на Земле можно найти точно так же, как мы нашли звездную величину Европы в задаче
(его нет во "Вселенной в числах", но его легко можно вычислить по имеющимся там данным о массе и средней плотности Юпитера). Видимую звездную величину Юпитера для наблюдателя на Земле можно найти точно так же, как мы нашли звездную величину Европы в задаче  . Если считать альбедо Юпитера равным 1, то найдем, что в противостоянии
. Если считать альбедо Юпитера равным 1, то найдем, что в противостоянии 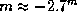 , что мало отличается от истинного значения
, что мало отличается от истинного значения  . Расстояние до
. Расстояние до  Cen -- 1.3 пк, или
Cen -- 1.3 пк, или 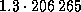 а.е. При наблюдении с такого расстояния видимая звездная величина Юпитера, если бы он находился в соединении с Солнцем, была бы равна
а.е. При наблюдении с такого расстояния видимая звездная величина Юпитера, если бы он находился в соединении с Солнцем, была бы равна
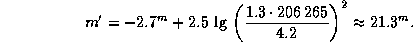
Число 4.2, появившееся здесь, -- это расстояние до Юпитера в противостоянии (в а.е.). В элонгации (для наблюдателя с  Cen) звездная величина Юпитера будет еще примерно на звездную величину больше из-за влияния его фазы. (Для наших целей аккуратно учитывать это обстоятельство нет нужды). Солнце же с
Cen) звездная величина Юпитера будет еще примерно на звездную величину больше из-за влияния его фазы. (Для наших целей аккуратно учитывать это обстоятельство нет нужды). Солнце же с  Cen имеет звездную величину
Cen имеет звездную величину 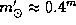 (проверьте).
(проверьте).
Таким образом, с одной стороны, угловое расстояние между Солнцем и Юпитером при наблюдении с  Cen достаточно, чтобы его можно было разрешить с помощью телескопа, но, с другой стороны, разность их звездных величин настолько велика, что слабый Юпитер скорее всего не будет виден вблизи гораздо более яркого Солнца (см. задачу
Cen достаточно, чтобы его можно было разрешить с помощью телескопа, но, с другой стороны, разность их звездных величин настолько велика, что слабый Юпитер скорее всего не будет виден вблизи гораздо более яркого Солнца (см. задачу  про галилеевы спутники Юпитера, точнее, про Европу).
про галилеевы спутники Юпитера, точнее, про Европу).
У наших коллег-астрономов с  Cen есть, впрочем, и другие пути обнаружить существование Юпитера -- длительные прецизионные измерения малых вариаций лучевой скорости и собственного движения Солнца (см. следующую задачу).
Cen есть, впрочем, и другие пути обнаружить существование Юпитера -- длительные прецизионные измерения малых вариаций лучевой скорости и собственного движения Солнца (см. следующую задачу).
 13.7 Для простоты решим задачу в предположении, что вокруг Солнца обращается только одна планета -- Юпитер с массой
13.7 Для простоты решим задачу в предположении, что вокруг Солнца обращается только одна планета -- Юпитер с массой 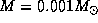 и орбитальной скоростью 13 км/с (см. задачу
и орбитальной скоростью 13 км/с (см. задачу  ). Отношение скоростей движения двух тел вокруг общего центра масс равно отношению их масс, в нашем случае -- 1:1000. Поэтому скорость движения центра Солнца составляет
). Отношение скоростей движения двух тел вокруг общего центра масс равно отношению их масс, в нашем случае -- 1:1000. Поэтому скорость движения центра Солнца составляет  м/с. Именно такой (или лучше хотя бы раза в два более высокой) должна быть точность определения лучевых скоростей, чтобы астроном-инопланетянин, живущий в плоскости эклиптики, по измерениям лучевых скоростей Солнца мог заподозрить существование Солнечной системы. Для астронома же, изучающего движение Солнца с
м/с. Именно такой (или лучше хотя бы раза в два более высокой) должна быть точность определения лучевых скоростей, чтобы астроном-инопланетянин, живущий в плоскости эклиптики, по измерениям лучевых скоростей Солнца мог заподозрить существование Солнечной системы. Для астронома же, изучающего движение Солнца с  Cen, амплитуда изменений его лучевой скорости будет меньше 13 м/с, а именно,
Cen, амплитуда изменений его лучевой скорости будет меньше 13 м/с, а именно, 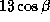 м/с
м/с  м/с. Здесь
м/с. Здесь 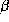 -- эклиптическая широта
-- эклиптическая широта  Cen (оцените ее самостоятельно по координатам
Cen (оцените ее самостоятельно по координатам  Cen или даже просто по звездной карте).
Cen или даже просто по звездной карте).
Интересно, что в 1995-1996 гг. у нескольких звезд, подобных Солнцу (70Vir, 47UMa и др.), были обнаружены планеты с массами, близкими к массе Юпитера. Чтобы сделать это выдающееся открытие, потребовалось разработать методику и создать специальную аппаратуру, позволившие измерять лучевые скорости с точностью порядка 10 м/с. Измерения велись в течение нескольких лет. С 1994 г. лучевые скорости стали измерять уже с точностью до 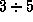 м/с. Хороший спринтер пробегает стометровку со скоростью около 10 м/с, а 3 м/с -- это бег трусцой.
м/с. Хороший спринтер пробегает стометровку со скоростью около 10 м/с, а 3 м/с -- это бег трусцой.
К моменту сдачи этого задачника в печать (август 1997 г.) наличие планет с массами от 0.5 до 13 масс Юпитера надежно установлено у 9 звезд.
Когда вы будете это читать, эти данные, несомненно, уже устареют. С состоянием дел на сегодняшний день (когда бы это ни происходило!) вы можете ознакомиться по постоянно обновляемой электронной "Энциклопедии внесолнечных планет", доступной в Интернете по адресу
http://www.obspm.fr/planets
Вернемся к нашей задаче. Искомую точность определения собственного движения для наблюдателя с  Cen оценим с помощью известного соотношения
Cen оценим с помощью известного соотношения

где  -- параллакс
-- параллакс  Cen. Так как
Cen. Так как 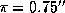 , то, подставляя
, то, подставляя 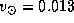 км/с, находим
км/с, находим  угл. сек./год.
угл. сек./год.
Обнаружение планет около нескольких звезд по измерениям лучевых скоростей, о чем говорилось выше, было подтверждено выявлением по данным, полученным ранее на астрометрическом спутнике HIPPARCOS, периодических изменений их собственных движений.
Межзвездная среда
 14.1 Межзвездное поглощение
14.1 Межзвездное поглощение 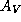 в полосе V связано с избытком цвета
в полосе V связано с избытком цвета 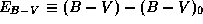 известным соотношением
известным соотношением

По условию задачи 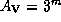 . Далее, истинный показатель цвета
. Далее, истинный показатель цвета 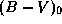 у звезды класса A0 равен нулю по определению показателя цвета. Поэтому искомый наблюдаемый показатель цвета равен
у звезды класса A0 равен нулю по определению показателя цвета. Поэтому искомый наблюдаемый показатель цвета равен
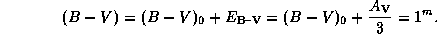
 14.2 Поглощаемое туманностью излучение центральной звезды -- это излучение в далеком ультрафиолете (лаймановский континуум,
14.2 Поглощаемое туманностью излучение центральной звезды -- это излучение в далеком ультрафиолете (лаймановский континуум, 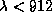
 ). При столь высокой температуре звезды большая часть ее излучения приходится на лаймановский континуум, и потому поглощается туманностью, ионизуя водород. В видимой же области спектра туманность прозрачна и для излучения центральной звезды, и для излучения просвечивающих сквозь нее далеких объектов.
). При столь высокой температуре звезды большая часть ее излучения приходится на лаймановский континуум, и потому поглощается туманностью, ионизуя водород. В видимой же области спектра туманность прозрачна и для излучения центральной звезды, и для излучения просвечивающих сквозь нее далеких объектов.
 14.3 Число фотонов, испускаемое за единицу времени с 1 см2 черного тела температуры T, равно
14.3 Число фотонов, испускаемое за единицу времени с 1 см2 черного тела температуры T, равно 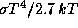 . Здесь
. Здесь 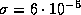 -- постоянная Стефана, а
-- постоянная Стефана, а  -- это средняя энергия одного чернотельного фотона (см. задачу
-- это средняя энергия одного чернотельного фотона (см. задачу  ). Так как температура звезды по условию задачи очень высока, почти все эти фотоны принадлежат лаймановскому континууму (
). Так как температура звезды по условию задачи очень высока, почти все эти фотоны принадлежат лаймановскому континууму ( 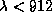
 ) и, значит, почти каждый из них может ионизовать атом водорода. Поэтому полное число ионизаций за 1 с близко к полному числу фотонов, излучаемых звездой за единицу времени:
) и, значит, почти каждый из них может ионизовать атом водорода. Поэтому полное число ионизаций за 1 с близко к полному числу фотонов, излучаемых звездой за единицу времени:
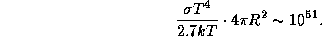
Чтобы облегчить вычисления, температура звезды, заданная в условии задачи, несколько завышена по сравнению с теми температурами, которые обычно имеют звезды, возбуждающие свечение газовых туманностей. Звезда класса O5 имеет температуру около 50000 K и испускает ежесекундно 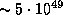 лаймановских фотонов. Это неплохо согласуется с нашей оценкой, если учесть, что двукратное различие в температуре дает различие в числе фотонов в 8 раз.
лаймановских фотонов. Это неплохо согласуется с нашей оценкой, если учесть, что двукратное различие в температуре дает различие в числе фотонов в 8 раз.
 14.4 Ионизовать водород способно лишь излучение с длиной волны
14.4 Ионизовать водород способно лишь излучение с длиной волны 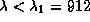
 , или с частотой
, или с частотой 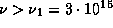 с
с 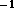 . Если считать, что спектр излучения звезды чернотельный, то искомая доля энергии равна
. Если считать, что спектр излучения звезды чернотельный, то искомая доля энергии равна
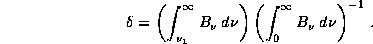
При 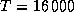 K для получения хорошей оценки величины
K для получения хорошей оценки величины 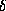 функцию Планка можно брать в приближении Вина:
функцию Планка можно брать в приближении Вина:
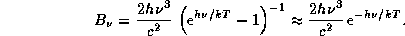
(Обосновать последнее утверждение, пользуясь решением задачи  ).
).
В первоначальной версии рукописи здесь стояло: "В результате несложных вычислений находим  ". Однако один из авторов настоял, что нужно воспользоваться этим случаем, чтобы проиллюстрировать, как грамотно вести оценочные расчеты.
". Однако один из авторов настоял, что нужно воспользоваться этим случаем, чтобы проиллюстрировать, как грамотно вести оценочные расчеты.
Введем безразмерную частоту 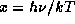 . Для водорода
. Для водорода 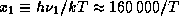 . Появившийся здесь коэффициент 160000 -- это энергия ионизации водорода (13.6 эВ) в температурной шкале. Это число очень полезно помнить. Оно часто появляется в самых разных астрофизических задачах. При
. Появившийся здесь коэффициент 160000 -- это энергия ионизации водорода (13.6 эВ) в температурной шкале. Это число очень полезно помнить. Оно часто появляется в самых разных астрофизических задачах. При 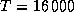 K, заданных в условии задачи, мы имеем поэтому
K, заданных в условии задачи, мы имеем поэтому  , так что
, так что

Ясно, что при  экспонента меняется гораздо быстрее, чем
экспонента меняется гораздо быстрее, чем 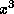 , и поэтому
, и поэтому
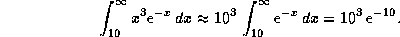
Это вполне приличная оценка (погрешность 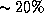 ). Ее можно уточнять, интегрируя несколько раз по частям и получая каждый раз все более точные результаты, но нам это вряд ли потребуется. Далее (см. задачу
). Ее можно уточнять, интегрируя несколько раз по частям и получая каждый раз все более точные результаты, но нам это вряд ли потребуется. Далее (см. задачу  ),
),

Итак,

Советуем запомнить, что с очень хорошей точностью  (на самом деле
(на самом деле 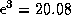 ) -- это часто помогает делать быстрые оценки. Поэтому
) -- это часто помогает делать быстрые оценки. Поэтому  , и мы получаем
, и мы получаем

Учить такой кухне прикидочных расчетов почему-то считается почти что неприличным -- а в результате студенты зря теряют массу времени попусту.
 14.5 Основная составляющая газовых туманностей и межзвездной среды -- это водород. В областях HII он практически полностью ионизован (отсюда и их название). Поэтому
14.5 Основная составляющая газовых туманностей и межзвездной среды -- это водород. В областях HII он практически полностью ионизован (отсюда и их название). Поэтому 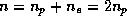 , где
, где 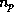 и
и  -- концентрации протонов и электронов, соответственно. Полное число ионизаций во всей области HII за единицу времени равно полному числу ионизующих фотонов, испускаемых возбуждающей звездой и поглощаемых в области HII. Оно, очевидно, не зависит от концентрации частиц в самой области HII. В стационарном состоянии полное число ионизаций должно равняться полному числу рекомбинаций. Рекомбинации происходят при столкновениях протонов и электронов, и потому число их в единице объема пропорционально
-- концентрации протонов и электронов, соответственно. Полное число ионизаций во всей области HII за единицу времени равно полному числу ионизующих фотонов, испускаемых возбуждающей звездой и поглощаемых в области HII. Оно, очевидно, не зависит от концентрации частиц в самой области HII. В стационарном состоянии полное число ионизаций должно равняться полному числу рекомбинаций. Рекомбинации происходят при столкновениях протонов и электронов, и потому число их в единице объема пропорционально 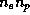 , или
, или  . Поэтому полное число рекомбинаций во всей области HII пропорционально
. Поэтому полное число рекомбинаций во всей области HII пропорционально 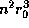 , где
, где  -- радиус области HII. С другой стороны, оно равно числу ионизаций -- фиксированному числу, определяемому параметрами возбуждающей звезды (ее радиусом и температурой). Итак,
-- радиус области HII. С другой стороны, оно равно числу ионизаций -- фиксированному числу, определяемому параметрами возбуждающей звезды (ее радиусом и температурой). Итак, 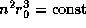 , откуда и следует, что
, откуда и следует, что  .
.
 14.6 Масса молекулы водорода H2 примерно равна удвоенной массе протона, т.е.
14.6 Масса молекулы водорода H2 примерно равна удвоенной массе протона, т.е. 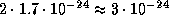 г. Объем облака по порядку величины есть
г. Объем облака по порядку величины есть 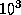 пк
пк 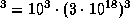 см
см 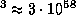 см3. Поэтому масса облака составляет
см3. Поэтому масса облака составляет 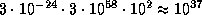 г
г 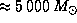 .
.
 14.7 Проходящее сквозь газ излучение ослабляется в e
14.7 Проходящее сквозь газ излучение ослабляется в e  раз, где
раз, где  -- оптическая толщина слоя газа. В центре линии L
-- оптическая толщина слоя газа. В центре линии L  она равна
она равна 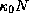 , где N -- полное число атомов водорода на луче зрения. Будем считать, что поглощение становится заметным, когда
, где N -- полное число атомов водорода на луче зрения. Будем считать, что поглощение становится заметным, когда 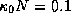 . Соответствующая масса на луче зрения составляет
. Соответствующая масса на луче зрения составляет  г/см2. Ошеломляющий результат, не правда ли? Вывод: спектральный анализ обладает колоссальной чувствительностью. Он позволяет выявлять присутствие совершенно ничтожных количеств вещества.
г/см2. Ошеломляющий результат, не правда ли? Вывод: спектральный анализ обладает колоссальной чувствительностью. Он позволяет выявлять присутствие совершенно ничтожных количеств вещества.
Галактика
 15.1 Расстояние до
15.1 Расстояние до  Cen -- это 4/3 пк, или
Cen -- это 4/3 пк, или 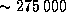 а.е. Поэтому Земля проходит такой путь за
а.е. Поэтому Земля проходит такой путь за 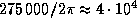 лет. Но это -- характерное расстояние между звездами в окрестности Солнца, а орбитальная скорость Земли 30 км/с -- того же порядка, что и пространственные скорости пекулярных движений звезд. Значит, относительное расположение близких звезд в пространстве, а потому и вид звездного неба как раз и меняется за такое время, т.е. за десятки тысяч лет.
лет. Но это -- характерное расстояние между звездами в окрестности Солнца, а орбитальная скорость Земли 30 км/с -- того же порядка, что и пространственные скорости пекулярных движений звезд. Значит, относительное расположение близких звезд в пространстве, а потому и вид звездного неба как раз и меняется за такое время, т.е. за десятки тысяч лет.
 15.2 Параллактический эллипс звезды имеет большую и малую полуоси, отношение которых
15.2 Параллактический эллипс звезды имеет большую и малую полуоси, отношение которых 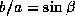 , где
, где 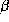 -- эклиптическая широта звезды. Эксцентриситет
-- эклиптическая широта звезды. Эксцентриситет  . Дева -- зодиакальное созвездие, и значит, у Спики (
. Дева -- зодиакальное созвездие, и значит, у Спики (  Vir)
Vir) 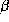 близко к нулю. Эксцентриситет почти равен единице, т.е. параллактический эллипс вырождается в отрезок. Далее, поскольку угол наклона эклиптики к экватору
близко к нулю. Эксцентриситет почти равен единице, т.е. параллактический эллипс вырождается в отрезок. Далее, поскольку угол наклона эклиптики к экватору 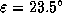 , а Полярная находится рядом с северным полюсом мира, ее эклиптическая широта
, а Полярная находится рядом с северным полюсом мира, ее эклиптическая широта 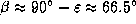 , откуда
, откуда  .
.
 15.3 Тангенциальная скорость звезды
15.3 Тангенциальная скорость звезды 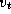 , выраженная в км/с, связана с ее собственным движением
, выраженная в км/с, связана с ее собственным движением  (угл. сек./год) следующим образом:
(угл. сек./год) следующим образом:

где r -- расстояние до звезды в парсеках, т.е. величина, обратная параллаксу  (в секундах дуги). Коэффициент пропорциональности 4.74 в этой формуле -- это множитель, переводящий скорости из а.е./год в км/с. Действительно, мы имеем
(в секундах дуги). Коэффициент пропорциональности 4.74 в этой формуле -- это множитель, переводящий скорости из а.е./год в км/с. Действительно, мы имеем 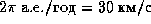 , так что
, так что  . Для "летящей звезды Барнарда" находим
. Для "летящей звезды Барнарда" находим
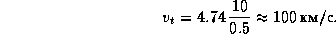
 15.4 Мы имеем 1а.е./год = 4.74 км/с
15.4 Мы имеем 1а.е./год = 4.74 км/с  км/с. Поэтому наша звезда проходит за год путь в
км/с. Поэтому наша звезда проходит за год путь в  а.е. С расстояния в 10 пк этот путь будет виден под углом 1". Следовательно,
а.е. С расстояния в 10 пк этот путь будет виден под углом 1". Следовательно, 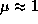 угл. сек./год.
угл. сек./год.
 15.5 Известно, что абсолютная звездная величина в полосе V равна нулю для звезд главной последовательности поздних подклассов B, примерно B7 -- B8. Мы не сильно ошибемся, приняв ее равной нулю и для звезд спектрального класса A0V. Так как видимая звездная величина Веги тоже близка к нулю, то в соответствии с определением абсолютной величины можно сделать вывод, что Вега находится на расстоянии около 10пк и, следовательно, ее параллакс порядка
15.5 Известно, что абсолютная звездная величина в полосе V равна нулю для звезд главной последовательности поздних подклассов B, примерно B7 -- B8. Мы не сильно ошибемся, приняв ее равной нулю и для звезд спектрального класса A0V. Так как видимая звездная величина Веги тоже близка к нулю, то в соответствии с определением абсолютной величины можно сделать вывод, что Вега находится на расстоянии около 10пк и, следовательно, ее параллакс порядка  .
.
На самом деле для Веги 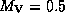 , и поэтому она находится немного ближе. Однако из формулы
, и поэтому она находится немного ближе. Однако из формулы

ясно, что ошибка на 0.5 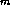 в абсолютной величине дает поправку к
в абсолютной величине дает поправку к  , равную лишь 0.1, т.е. множитель 0.8 в самом расстоянии r. И действительно, расстояние до Веги составляет 8.1 пк.
, равную лишь 0.1, т.е. множитель 0.8 в самом расстоянии r. И действительно, расстояние до Веги составляет 8.1 пк.
 15.6
15.6
Сверхновая вспыхнула около 950 лет назад (точнее, порожденное взрывом излучение достигло Земли 950 лет назад), а скорость расширения туманности 1200 км/с. Поэтому характерный линейный размер современного Краба 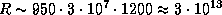 км, или 1 пк. Соответствующий угловой размер составляет
км, или 1 пк. Соответствующий угловой размер составляет 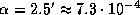 рад. Отсюда расстояние
рад. Отсюда расстояние 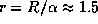 кпк (на самом деле -- чуть больше, около 2 кпк).
кпк (на самом деле -- чуть больше, около 2 кпк).
 15.7 Равенство периодов цефеид влечет равенство светимостей. Поэтому разность видимых звездных величин обусловлена только разностью расстояний
15.7 Равенство периодов цефеид влечет равенство светимостей. Поэтому разность видимых звездных величин обусловлена только разностью расстояний 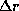 . Последняя не превосходит диаметра туманности Андромеды, который по порядку величины равен диаметру нашей Галактики:
. Последняя не превосходит диаметра туманности Андромеды, который по порядку величины равен диаметру нашей Галактики:  кпк. Разность звездных величин вычислим по формуле задачи
кпк. Разность звездных величин вычислим по формуле задачи  :
:
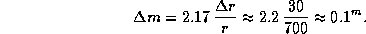
Здесь мы молчаливо приняли, что галактика M31 видна почти с ребра. Это действительно так (см. задачу  ).
).
Разность в 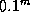 слишком мала, чтобы по ней можно было бы уверенно сказать, которая из цефеид ближе к нам.
слишком мала, чтобы по ней можно было бы уверенно сказать, которая из цефеид ближе к нам.
 15.8 Поскольку пять звезд, о которых идет речь, расположены близко друг к другу на небе, схожи по блеску и цвету и обладают практически одинаковыми собственными движениями и лучевыми скоростями, естественно предположить, что они образуют группу пространственно близких звезд. Фактически они являются членами одного рассеянного скопления и потому находятся примерно на одном и том же расстоянии от нас. Для оценки этого расстояния заметим прежде всего, что звезды ковша белые, их спектральный класс близок к A0. Поэтому их абсолютная величина должна быть близка к нулю (см. задачу
15.8 Поскольку пять звезд, о которых идет речь, расположены близко друг к другу на небе, схожи по блеску и цвету и обладают практически одинаковыми собственными движениями и лучевыми скоростями, естественно предположить, что они образуют группу пространственно близких звезд. Фактически они являются членами одного рассеянного скопления и потому находятся примерно на одном и том же расстоянии от нас. Для оценки этого расстояния заметим прежде всего, что звезды ковша белые, их спектральный класс близок к A0. Поэтому их абсолютная величина должна быть близка к нулю (см. задачу  ). Видимая же их величина примерно
). Видимая же их величина примерно 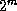 -- звезды ковша яркие. Из формулы
-- звезды ковша яркие. Из формулы

при M=0 и m=2 находим, что 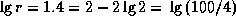 , откуда
, откуда 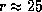 пк.
пк.
Мы получили очень хорошую оценку расстояния. И на самом деле расстояние "до ковша" -- 25 пк.
 15.9 Источники УН-диапазона либо являются близкими (расстояния до
15.9 Источники УН-диапазона либо являются близкими (расстояния до 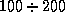 пк), либо находятся на космологических расстояниях (последняя возможность имеется только в том случае, если Галактика прозрачна для УН-излучения). Расстояния до ИН-источников -- сотни парсек или несколько килопарсек (но заметно меньше расстояния до центра Галактики).
пк), либо находятся на космологических расстояниях (последняя возможность имеется только в том случае, если Галактика прозрачна для УН-излучения). Расстояния до ИН-источников -- сотни парсек или несколько килопарсек (но заметно меньше расстояния до центра Галактики).
В течение тридцати лет астрономы время от времени фиксировали со спутников кратковременные всплески 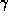 -излучения. Всего было зарегистрировано более 3000 таких событий. Распределение источников
-излучения. Всего было зарегистрировано более 3000 таких событий. Распределение источников 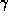 -всплесков по небу оказалось более или менее равномерным -- как и у выдуманных нами источников УН-диапазона. Все тридцать лет шла дискуссия о том, являются ли источники
-всплесков по небу оказалось более или менее равномерным -- как и у выдуманных нами источников УН-диапазона. Все тридцать лет шла дискуссия о том, являются ли источники 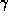 -всплесков близкими или, наоборот, очень далекими ("космологическими") объектами. В мае 1997 г. проблема была, наконец, решена, когда один из
-всплесков близкими или, наоборот, очень далекими ("космологическими") объектами. В мае 1997 г. проблема была, наконец, решена, когда один из 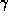 -всплесков был надежно отождествлен с далеким внегалактическим объектом (параметр красного смещения z = 0.84). Оказалось, что
-всплесков был надежно отождествлен с далеким внегалактическим объектом (параметр красного смещения z = 0.84). Оказалось, что 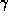 -всплески -- это самые мощные из всех взрывов, которые до сих пор наблюдались во Вселенной (Большой Взрыв -- не в счет, наблюдаются лишь его последствия, а не он сам). Это одно из крупнейших астрономических открытий последнего времени.
-всплески -- это самые мощные из всех взрывов, которые до сих пор наблюдались во Вселенной (Большой Взрыв -- не в счет, наблюдаются лишь его последствия, а не он сам). Это одно из крупнейших астрономических открытий последнего времени.
 15.10 Приравниваем центробежную силу к силе притяжения, что дает
15.10 Приравниваем центробежную силу к силе притяжения, что дает

Мы имеем v=250 км/с, r=8 кпк. В результате находим, что  . Очевидно, что это нижняя оценка. Действительная масса Галактики, возможно, на порядок больше.
. Очевидно, что это нижняя оценка. Действительная масса Галактики, возможно, на порядок больше.
Для многих спиральных галактик зависимость скорости вращения v от расстояния до центра r была тщательно измерена, в частности, по доплеровским смещениям радиолинии нейтрального водорода 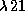 см. Оказалось, что на больших расстояниях -- там, где видимый в оптике звездный диск уже кончается -- зависимость
см. Оказалось, что на больших расстояниях -- там, где видимый в оптике звездный диск уже кончается -- зависимость  не выполняется. Кривые, дающие v в функции r, как говорят, плоские: начиная с расстояния в несколько килопарсеков, грубо говоря
не выполняется. Кривые, дающие v в функции r, как говорят, плоские: начиная с расстояния в несколько килопарсеков, грубо говоря 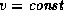 . Это свидетельствует о том, что в спиральных галактиках на значительных расстояниях от центра, в том числе и там, где звездный диск уже перестает быть виден, находится значительная масса. Природа этой так называемой скрытой массы -- "скрытой" потому, что она не дает практически никакого вклада в излучение -- является по сей день предметом жарких споров.
. Это свидетельствует о том, что в спиральных галактиках на значительных расстояниях от центра, в том числе и там, где звездный диск уже перестает быть виден, находится значительная масса. Природа этой так называемой скрытой массы -- "скрытой" потому, что она не дает практически никакого вклада в излучение -- является по сей день предметом жарких споров.
Дата добавления: 2019-01-14; просмотров: 233; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
