Основные характеристики звезд 8 страница
Всемирное тяготение
 5.1 Солнечная система разрушится. Планеты улетят от Солнца по параболам, поскольку скорость их движения по первоначальным (круговым) орбитам в точности равна параболической скорости при уменьшенной вдвое массе центрального тела. Возможно, Солнце сохранит Меркурий, Марс и Плутон. Однако если бы эта катастрофа случилась с Солнцем в течение нескольких ближайших лет (чего определенно не произойдет), то Плутон тоже наверняка был бы потерян -- он сейчас находится близ перигелия своей заметно некруговой орбиты. А про Марс и про Меркурий заранее сказать что-то трудно. Все будет зависеть от их положения на орбитах в тот момент, когда Солнце "похудеет". Если они окажутся близ афелиев, то сохранятся около Солнца, если же будут близ перигелиев, то улетят от него навсегда.
5.1 Солнечная система разрушится. Планеты улетят от Солнца по параболам, поскольку скорость их движения по первоначальным (круговым) орбитам в точности равна параболической скорости при уменьшенной вдвое массе центрального тела. Возможно, Солнце сохранит Меркурий, Марс и Плутон. Однако если бы эта катастрофа случилась с Солнцем в течение нескольких ближайших лет (чего определенно не произойдет), то Плутон тоже наверняка был бы потерян -- он сейчас находится близ перигелия своей заметно некруговой орбиты. А про Марс и про Меркурий заранее сказать что-то трудно. Все будет зависеть от их положения на орбитах в тот момент, когда Солнце "похудеет". Если они окажутся близ афелиев, то сохранятся около Солнца, если же будут близ перигелиев, то улетят от него навсегда.
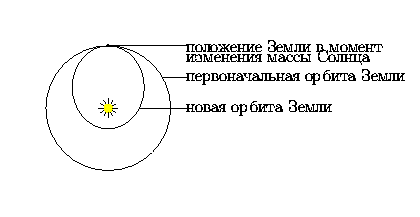
 5.2 В момент внезапного увеличения массы Солнца Земля начинает испытывать вдвое большую, чем прежде, силу притяжения со стороны Солнца. Следовательно, она перейдет с круговой орбиты на эллиптическую, целиком лежащую внутри прежней орбиты (см. рис. на следующей странице). Таким образом, в момент схода с круговой орбиты Земля будет находиться в афелии своей новой эллиптической орбиты.
5.2 В момент внезапного увеличения массы Солнца Земля начинает испытывать вдвое большую, чем прежде, силу притяжения со стороны Солнца. Следовательно, она перейдет с круговой орбиты на эллиптическую, целиком лежащую внутри прежней орбиты (см. рис. на следующей странице). Таким образом, в момент схода с круговой орбиты Земля будет находиться в афелии своей новой эллиптической орбиты.
Интегралы энергии, описывающие движение Земли в поле центрального тела с массами, равными M и 2M, имеют соответственно следующий вид:
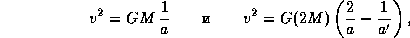
где a -- первоначальное и  -- новое значение большой полуоси орбиты Земли (после того как масса Солнца внезапно увеличилась вдвое). Сравнивая эти два выражения между собой, находим, что
-- новое значение большой полуоси орбиты Земли (после того как масса Солнца внезапно увеличилась вдвое). Сравнивая эти два выражения между собой, находим, что  .
.
|
|
|
Найдем период обращения Земли по новой орбите. По третьему закону Кеплера имеем

откуда

Эксцентриситет новой орбиты найдем из соотношения a = a'(1+e'), откуда e'=0.5.
 5.3 Из приравнивания центробежной силы
5.3 Из приравнивания центробежной силы  к силе тяготения
к силе тяготения  следует, что
следует, что  (значение постоянной подсчитайте сами). Средние же плотности всех тел Солнечной системы отличаются меньше, чем на порядок. Они заключены между 0.7 г/см3 (Сатурн; соответствующее время облета -- 4.2 часа) и 5.5 г/см3 (Земля; облетев Землю за полтора часа, Гагарин установил тем самым первый в истории и по сей день единственный межпланетный рекорд).
(значение постоянной подсчитайте сами). Средние же плотности всех тел Солнечной системы отличаются меньше, чем на порядок. Они заключены между 0.7 г/см3 (Сатурн; соответствующее время облета -- 4.2 часа) и 5.5 г/см3 (Земля; облетев Землю за полтора часа, Гагарин установил тем самым первый в истории и по сей день единственный межпланетный рекорд).
Время облета Солнца, а потому одновременно и верхняя оценка возможного минимального периода осевого вращения звезд типа Солнца, в 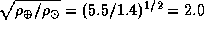 раза больше минимального времени облета Земли и составляет, таким образом, всего около 3 часов! Не правда ли, удивительно? За это время проходится путь
раза больше минимального времени облета Земли и составляет, таким образом, всего около 3 часов! Не правда ли, удивительно? За это время проходится путь  млн км, скорость полета близка к 400 км/с -- в
млн км, скорость полета близка к 400 км/с -- в  раза меньше скорости убегания с "поверхности" Солнца.
раза меньше скорости убегания с "поверхности" Солнца.
У типичного белого карлика 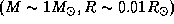 средняя плотность
средняя плотность 
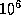 г/см3, и потому время облета порядка 10 секунд, скорость же движения при этом всего
г/см3, и потому время облета порядка 10 секунд, скорость же движения при этом всего  км/с ("всего" -- это значит, что хотя по повседневным меркам она и велика, но все же
км/с ("всего" -- это значит, что хотя по повседневным меркам она и велика, но все же  .
.
|
|
|
Облет нейтронной звезды 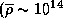 г/см3) занял бы всего несколько миллисекунд и (при радиусе звезды
г/см3) занял бы всего несколько миллисекунд и (при радиусе звезды  км) происходил бы со скоростью во многие десятки тысяч км/с. Ясно, что, изучая нейтронные звезды, мы находимся у самой границы применимости классической механики. Релятивистские поправки для нейтронных звезд должны быть уже очень заметными.
км) происходил бы со скоростью во многие десятки тысяч км/с. Ясно, что, изучая нейтронные звезды, мы находимся у самой границы применимости классической механики. Релятивистские поправки для нейтронных звезд должны быть уже очень заметными.
Примечание (для "эрудитов"). То, что 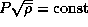 , следует и из обобщенного третьего закона Кеплера
, следует и из обобщенного третьего закона Кеплера  . Однако не-эрудиты знают лишь, что
. Однако не-эрудиты знают лишь, что 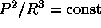 , помнить же выражение для постоянной -- это и есть "эрудиция".
, помнить же выражение для постоянной -- это и есть "эрудиция".
 5.4 Из интеграла энергии
5.4 Из интеграла энергии

и выражений для расстояний в перигелии и в афелии

следует, что отношение соответствующих скоростей есть

Если оно равно 3, то e=0.5.
 5.5 Пусть P -- период обращения в годах, r -- радиус орбиты в а.е. и v -- скорость движения по орбите в км/с. Поскольку орбитальная скорость Земли равна 30 км/с, то мы имеем, очевидно,
5.5 Пусть P -- период обращения в годах, r -- радиус орбиты в а.е. и v -- скорость движения по орбите в км/с. Поскольку орбитальная скорость Земли равна 30 км/с, то мы имеем, очевидно,

С другой стороны, по третьему закону Кеплера 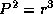 , и поэтому
, и поэтому

так что, например, Юпитер (r=5) движется по орбите со скоростью  км/с.
км/с.
 5.6 Запишем интеграл энергии для кометы, находящейся на гелиоцентрическом расстоянии Земли:
5.6 Запишем интеграл энергии для кометы, находящейся на гелиоцентрическом расстоянии Земли:
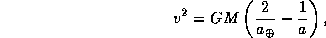
где  -- большая полуось орбиты Земли, 1 а.е. Круговая скорость на орбите Земли есть
-- большая полуось орбиты Земли, 1 а.е. Круговая скорость на орбите Земли есть

Так как по условию  , большая полуось оказывается равной
, большая полуось оказывается равной

Период обращения находится отсюда по третьему закону Кеплера:
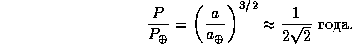
Он тот же, что и при падении на притягивающий центр по прямой, см. задачу  . Из условия задачи следует, что комета на расстоянии 1 а.е. находится в афелии своей орбиты, так что афелийное расстояние есть
. Из условия задачи следует, что комета на расстоянии 1 а.е. находится в афелии своей орбиты, так что афелийное расстояние есть  а.е. Но
а.е. Но  , отсюда эксцентриситет
, отсюда эксцентриситет

Следовательно, перигелийное расстояние будет чрезвычайно малым:

Это, кстати, около 750000 км, а значит, комета в перигелии почти "зацепит" Солнце. Такие кометы, "царапающие Солнце", неоднократно наблюдались.
|
|
|
 5.7 Расстояния в перигее и в апогее
5.7 Расстояния в перигее и в апогее

дают большую полуось орбиты спутника

и ее эксцентриситет

Период обращения по третьему закону Кеплера равен

В эту формулу можно подставить числа, но вычисления можно существенно сократить следующим образом. Мы знаем, что низколетящий спутник совершает виток вокруг Земли за  1.5 часа ("гагаринское время"). Это значит, что при полуоси
1.5 часа ("гагаринское время"). Это значит, что при полуоси  период
период  . Записав третий закон Кеплера в относительной форме
. Записав третий закон Кеплера в относительной форме

получаем

Действительно, "Молния" -- полусуточный спутник.
 5.8 Большая полуось орбиты Земли -- 1 а.е., Марса -- 1.5 а.е. Период обращения Земли равен 1 году. Большая полуось гомановского эллипса равна, очевидно, полусумме радиусов орбит Земли и Марса: a=1.25 а.е. По третьему закону Кеплера период обращения для гомановской орбиты в годах равен
5.8 Большая полуось орбиты Земли -- 1 а.е., Марса -- 1.5 а.е. Период обращения Земли равен 1 году. Большая полуось гомановского эллипса равна, очевидно, полусумме радиусов орбит Земли и Марса: a=1.25 а.е. По третьему закону Кеплера период обращения для гомановской орбиты в годах равен

Искомое время перелета составляет половину периода обращения, т.е. около 8 месяцев.
|
|
|
 5.9 Сидерический период вращения Солнца на экваторе
5.9 Сидерический период вращения Солнца на экваторе  , таков же период обращения космического аппарата на гелиостационарной орбите. Для Земли период обращения
, таков же период обращения космического аппарата на гелиостационарной орбите. Для Земли период обращения  год, большая полуось орбиты
год, большая полуось орбиты  а.е. По третьему закону Кеплера, выражая P и a в годах и в а.е., соответственно, имеем
а.е. По третьему закону Кеплера, выражая P и a в годах и в а.е., соответственно, имеем  , откуда находим радиус гелиостационарной орбиты:
, откуда находим радиус гелиостационарной орбиты:

Без всяких вычислений можно было сразу утверждать, что гелиостационарная орбита лежит внутри орбиты Меркурия, период обращения которого вокруг Солнца равен 88 суткам, что существенно больше периода осевого вращения Солнца.
 5.10 Как следует из закона сохранения энергии, какую бы скорость ни имело тело на границе сферы действия Луны, при касании лунной поверхности она не может быть меньше скорости убегания с поверхности Луны, 2.4 км/с.
5.10 Как следует из закона сохранения энергии, какую бы скорость ни имело тело на границе сферы действия Луны, при касании лунной поверхности она не может быть меньше скорости убегания с поверхности Луны, 2.4 км/с.
 5.11 Величины, относящиеся к Юпитеру, будем отмечать индексом J. Тогда отношение светимостей
5.11 Величины, относящиеся к Юпитеру, будем отмечать индексом J. Тогда отношение светимостей  равно доле поверхности сферы радиуса 5 а.е., которую занимает диск Юпитера:
равно доле поверхности сферы радиуса 5 а.е., которую занимает диск Юпитера:

где  -- радиус Юпитера в км. Учитывая, что радиус Юпитера
-- радиус Юпитера в км. Учитывая, что радиус Юпитера  , мы получаем
, мы получаем

Искомый темп аккреции оценим по очевидной формуле (ср. решение задачи  )
)

где  км/с -- вторая космическая скорость для Юпитера.
км/с -- вторая космическая скорость для Юпитера.
Таким образом, если бы такая аккреция имела место, за время жизни Солнечной системы 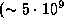 лет) масса Юпитера заметно не изменилась бы. Здесь уместно напомнить, что действительная светимость Юпитера примерно вдвое выше той, которая обеспечивается приходящим от Солнца излучением. Однако источник этой энергии следует искать в самом Юпитере, а не в аккреции.
лет) масса Юпитера заметно не изменилась бы. Здесь уместно напомнить, что действительная светимость Юпитера примерно вдвое выше той, которая обеспечивается приходящим от Солнца излучением. Однако источник этой энергии следует искать в самом Юпитере, а не в аккреции.
 5.12 Энергия, необходимая для доставки пылесоса на Луну, примерно равна
5.12 Энергия, необходимая для доставки пылесоса на Луну, примерно равна  , где
, где  и
и  -- первая и вторая космические скорости, m -- масса пылесоса. Энергия, выделяющаяся при работе пылесоса, равна PT, где P -- мощность его мотора, T -- время работы. Если принять P = 500 Вт
-- первая и вторая космические скорости, m -- масса пылесоса. Энергия, выделяющаяся при работе пылесоса, равна PT, где P -- мощность его мотора, T -- время работы. Если принять P = 500 Вт  эрг/с, m = 5 кг, то получим:
эрг/с, m = 5 кг, то получим:  с
с  суток. Всего нужно, таким образом, около 80 кВт
суток. Всего нужно, таким образом, около 80 кВт  час, а это стоит (в ценах конца 1996 г.) всего каких-то
час, а это стоит (в ценах конца 1996 г.) всего каких-то  руб. См. также задачу
руб. См. также задачу  .
.
 5.13 Ответ таков: предельный радиус составляет около
5.13 Ответ таков: предельный радиус составляет около  км, если прыгать вверх, не разбегаясь, и несколько больше, если сначала разбежаться. Вот соответствующий расчет.
км, если прыгать вверх, не разбегаясь, и несколько больше, если сначала разбежаться. Вот соответствующий расчет.
Ясно, что в момент отрыва от поверхности астероида прыгун должен развить вторую космическую скорость

Второе выражение для v, безусловно, больше подходит для наших целей, так как среднюю плотность астероида оценить не составляет труда:  заключено между 1 г/см3 (лед) и 8 г/см3 (железо). Мы в дальнейшем будем брать
заключено между 1 г/см3 (лед) и 8 г/см3 (железо). Мы в дальнейшем будем брать  г/см3. Итак,
г/см3. Итак,

Вертикальную составляющую скорости прыгуна при прыжке на Земле можно оценить по формуле

где g -- земное ускорение силы тяжести и h -- высота, на которую центр тяжести поднимается в прыжке. В качестве разумной оценки возьмем h=1 м (тогда прыгун преодолеет планку на высоте  см -- космонавт, оказавшийся на астероиде, надо думать, хорошо тренирован).
см -- космонавт, оказавшийся на астероиде, надо думать, хорошо тренирован).
В итоге радиус астероида, с которого можно, подскочив вверх, улететь в открытый космос, оказывается равен

Если, однако, перед прыжком космонавт разбежится, то он сумеет спрыгнуть и с тела большего размера. На астероиде разбег дает неожиданный эффект, с которым земные спортсмены не знакомы. На астероиде размером в несколько километров, имея хорошие шиповки, легко разбежаться до первой космической скорости (проверьте!). А тогда за счет прыжка вверх нужно будет преодолевать меньший потенциальный барьер.
 5.14 У спутника, движущегося по круговой орбите, центробежная сила уравновешивает силу притяжения, что дает
5.14 У спутника, движущегося по круговой орбите, центробежная сила уравновешивает силу притяжения, что дает

Обозначим через  и
и 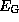 , соответственно, кинетическую и потенциальную энергию в расчете на единицу массы спутника. Тогда последнее равенство можно записать также так:
, соответственно, кинетическую и потенциальную энергию в расчете на единицу массы спутника. Тогда последнее равенство можно записать также так:

Пусть, далее, E -- полная энергия спутника:

Эти соотношения дают

откуда  . Это равенство означает, что, действительно, темп потерь энергии на трение о воздух
. Это равенство означает, что, действительно, темп потерь энергии на трение о воздух  (отрицательная величина -- энергия расходуется) равен темпу прироста кинетической энергии спутника
(отрицательная величина -- энергия расходуется) равен темпу прироста кинетической энергии спутника 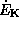 (положительному!). Откуда же эта энергия черпается? Очевидно, что из потенциальной энергии -- другого источника нет. Действительно, так как
(положительному!). Откуда же эта энергия черпается? Очевидно, что из потенциальной энергии -- другого источника нет. Действительно, так как  (см. выше), то
(см. выше), то 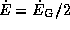 , так что спутник получает лишь половину выделяющейся гравитационной энергии, вторая же половина переходит в тепло.
, так что спутник получает лишь половину выделяющейся гравитационной энергии, вторая же половина переходит в тепло.
Дата добавления: 2019-01-14; просмотров: 178; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
