Основные характеристики звезд 10 страница

Точное значение есть

См. об этом следующую задачу.

5.20 Ответ: По баллистике получается .

Решение: Найдем сначала наибольшую высоту, на которую поднимется ракета. Начальная скорость, по условию, равна первой космической:

где M и R -- масса и радиус Земли. Расстояние верхней точки траектории от центра Земли можно найти из того условия, что кинетическая энергия ракеты на старте оказывается к моменту ее остановки израсходованной на увеличение потенциальной энергии:

Из двух написанных формул следует, что , так что ракета, вертикально запущенная с первой космической скоростью, поднимается над поверхностью на высоту, равную радиусу тела, с которого ее запускали, в нашей "батальной" истории -- Земли.

Если бы вся масса Земли была сосредоточена в ее центре, то падающая ракета достигла бы этого притягивающего центра, облетела его и мгновенно полетела бы назад. Она стала бы совершать периодическое движение по отрезку длины 2R, который можно рассматривать как вырожденный эллипс с эксцентриситетом e=1. Верхняя точка, которой достигает ракета, -- это афелий, или точнее апогей этой орбиты. Здесь происходит остановка, после чего начинается падение на притягивающий центр. Скорость монотонно возрастает от нуля при r=2R до 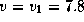км/с при r=R и, продолжая расти, становится (формально) бесконечной, когда достигается притягивающий центр. Ясно, что для решения задачи надо найти время свободного падения с высоты до r=R. Удвоив его, получим полное время полета ракеты от ее запуска до поражения цели.

Если вы немного знаете небесную механику, нахождение этого времени труда не составит. Достаточно вспомнить геометрический смысл эксцентрической аномалии E и сообразить, что в момент, когда ракета поражает цель, . Применив уравнение Кеплера с e=1, найдем среднюю аномалию:

Поэтому время полета от апогея до поверхности Земли равно

а время полета от запуска до цели составит

Дадим теперь другое решение, не требующее знания уравнения Кеплера и понятий "эксцентрическая" и "средняя аномалии". Впрочем, фактически они появятся и в этом решении. Прежде всего заметим, что полный период движения по прямолинейному отрезку длины 2R (рассматриваемому как эллипс с полуосью a=R и эксцентриситетом e=1) равен времени облета Земли на низколетящем спутнике (та же полуось, но e=0), т.е. составляет гагаринские полтора часа. Более точное значение таково:

Ясно, что, падая на центр и медленно разгоняясь, тело будет находиться на расстоянии r>R большую часть этого времени. Вторая половина пути (r<R) должна преодолеваться гораздо быстрее первой, так как скорость тут уже велика. Если бы весь путь проходился с постоянной скоростью, то запуск надо было бы произвести за минуты до момента падения. Пока наши рассуждения дали очень грубую оценку времени запуска ракеты: где-то между 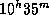и 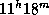(вероятно, все же ближе к первому числу, чем ко второму). Если бы было известно, что вражеская подлодка проведет на полюсе хотя бы час, больше ничего считать было бы не нужно.

[Фактически в предыдущей задаче мы уже довольно подробно разбирали вопрос об оценке интересующего нас времени полета ракеты. Если воспользоваться полученным там результатом, то можно заключить, что пуск ракеты надо произвести между 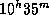и . Увы, временная вилка все еще слишком велика для нас. Придется решать задачу точно.]

Будем исходить из интеграла энергии

Введем безразмерное расстояние

и безразмерное время

Тогда

Это естественные для разбираемой задачи переменные (см. предыдущую задачу). В этих переменных интеграл энергии принимает вид

Будем отсчитывать время от момента прохождения "перигея" (т.е. от момента пролета мимо точечной массы), так что x=0 при 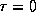. Тогда из последнего соотношения находим

Этой формулой определяется закон движения по прямолинейной орбите: по заданному в принципе можно (хотя и не в явном виде) найти соответствующее ему x, т.е. расстояние движущегося тела от притягивающего центра. Фактически полученное только что уравнение, связывающее x и , есть записанное в хорошо "зашифрованном" виде уравнение Кеплера при e=1. Точнее говоря, как мы сейчас увидим, оно эквивалентно ему.

Чтобы убедиться в этом, вычислим стоящий слева интеграл. Полагая

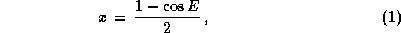
легко находим, что

Так как время отсчитывается от момента сближения точки с притягивающим центром, то мы заключаем, что

Формулы (1) и (2) задают закон движения, т.е. зависимость x от в параметрической форме.

Непосредственно для решения задачи закон движения нам не нужен -- достаточно найти, за какое время точка проходит ту половину отрезка, где она движется быстро. Полагая в (1) и (2) , находим, что при x=1/2 значение равно

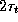Безразмерное время, которое займет полет ракеты, есть время полного оборота, равное , уменьшенное на , что равно . Это составляет полного времени движения по орбите.

Итак, полет ракеты займет время, равное

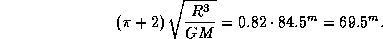
Поэтому ракету можно запускать в . Однако опытный командир нашей подлодки поступит не так. Он отдаст команду "Пуск!" в , чтобы поразить вражескую субмарину примерно посередине времени ее предполагаемого пребывания на поверхности. В самом деле, "они" ведь могут либо чуть запоздать, либо почему-то чуть раньше уйти под лед. Вот он, тот самый здравый смысл, о котором мы говорили в самом начале в наших методических заметках.

Казалось бы, все сделано, задача решена, ответ найден. Несколько комментариев будут, однако, далеко не лишними. Первое замечание совсем простое. Кривая, изображающая полученную выше зависимость x от -- это обычная циклоида. Второе замечание мелкое, но методически полезное. Почему мы положили 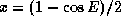, а не сделали более "естественную" рационализирующую подстановку , в которой всегда фигурируют половинные углы? Причин две. Во-первых, такова историческая традиция. Во-вторых, поскольку полученные формулы используются для вычислений по схеме: "Задаем E. По нему вычисляем x и ", то при использовании нашей подстановки требуется на одно умножение меньше -- хоть небольшая, но все же экономия. Когда компьютеров еще не было, с этим нельзя было не считаться. Однако и сегодня вычисления следует организовывать так, чтобы по возможности минимизировать число умножений.

Земля, Луна и планеты

6.1 В подсолнечной точке темп притока энергии равен 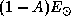, где -- альбедо Луны, эрг/(см²c) -- солнечная постоянная. Отток энергии происходит за счет излучения нагретого поверхностного слоя почвы (в ИК-диапазоне), темп которого равен , где -- постоянная Стефана (индекс s у 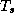-- от surface, т.е. поверхность). Приравнивая темпы нагрева и охлаждения, получаем

откуда K, или 115^o по Цельсию, так что босиком не походишь -- обожжешь ступни. Эта оценка слегка завышена. Она была бы строго верна, если бы Луна всегда была обращена одной стороной к Солнцу (а не к Земле). Однако так как вращение Луны вокруг оси происходит медленно, ошибка должна быть невелика.

6.2 Будут очень-очень сильно мерзнуть ноги. Из-за различия в альбедо отношение абсолютных температур на месте, залитом краской, и на соседнем лунном грунте будет близко к (см. формулу в решении задачи ). Если у обычного лунного грунта (альбедо A=0.07) в подсолнечной точке температура равна 388 K (см. предыдущую задачу), то в луже краски она будет K, или 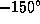по Цельсию -- жуткий мороз! (А железный лист в условии задачи зачем понадобился, как вы думаете?)

6.3 На единицу поверхности планеты в "подсолнечной" точке падает поток , где -- радиус звезды, а d -- расстояние от нее до планеты. Из этого потока доля 1-A, поглощаемая поверхностью планеты, идет на ее нагрев. Приравнивая скорости притока и оттока тепла в "подсолнечной" точке, получаем

откуда для температуры в "подсолнечной" точке находим

Значение d найдем, приравнивая центробежную силу к силе притяжения планеты к звезде, что дает

где P -- период обращения планеты. Эрудиты, помнящие наизусть третий закон Кеплера, точнее, коэффициент пропорциональности в соотношении 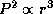, могли бы написать это сразу.

Подставляя это выражение для d через P в формулу для , получаем

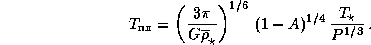
Единственный параметр звезды, помимо ее температуры, который входит в эту формулу, это ее средняя плотность .

По условию задачи, температура на планете должна быть такой же, как на Луне. Последняя, очевидно, также дается полученным только что выражением, в котором следует положить 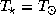и , а P взять равным 1 году. Приравнивая температуры на планете и на Луне, для периода обращения планеты в годах получаем следующее простое выражение:

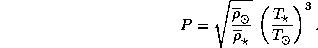
Подставив числа, найдем, что, например, для звезды класса A0 K, период составляет около 10 лет.

Далее, так как величина падающего потока пропорциональна косинусу зенитного расстояния звезды z, то зависимость температуры на поверхности лишенной атмосферы планеты от z имеет вид

Выражение для P, полученное выше, позволяет немного пофантазировать о жизни на других мирах. Очевидно, что оно дает продолжительность года на планете с тем же температурным режимом, что и у Земли, которая обращается вокруг звезды с известной температурой и средней плотностью. Данные о и для звезд разных спектральных классов можно найти у Аллена [1]. Оказывается, например, что если бы Земля обращалась не вокруг Солнца, а вокруг звезды класса M5V ( 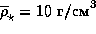, K), то чтобы на ней можно было сносно жить -- не замерзнуть и не изжариться -- продолжительность года должна была бы составлять всего земных суток. Впадать в долгую зимнюю спячку медведям не удалось бы!

6.4 Для ионизации атома водорода требуется энергия эВ. Поэтому число атомов водорода , которое может быть ионизовано за счет кинетической энергии движения Земли, равно

где v=30 км/с -- скорость движения Земли, M -- ее масса. Далее, число атомов водорода в газовом облаке с массой M равно 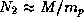, где -- масса протона. Подставляя известные числовые значения физических величин, находим отношение

которое оказывается хотя и порядка, но все же меньше единицы. Таким образом, кинетической энергии движения Земли по орбите не достаточно, чтобы ионизовать облако водорода с массой, равной массе Земли.

Дадим другой вариант решения. Как показывается в задаче , нуклон, движущийся со скоростью 1500 км/с, имеет энергию около 10кэВ. При скорости движения в 30 км/с кинетическая энергия нуклона будет в раз меньше, или около 4эВ, что составляет 0.3 от энергии связи атома водорода (13.6эВ). Отсюда непосредственно следует, в согласии с полученным выше, что кинетической энергии движения Земли хватит на ионизацию массы водорода, составляющей 0.3 ее собственной массы.

Кинетическая энергия протона равна 1 эВ, если он движется со скоростью км/с.

6.5 Один способ решения см. во вводных замечаниях к задачнику. А вот другое решение. Всякий знает, что атмосферное давление составляет г/см². Поэтому масса столба воздуха сечением 1 см² равна г. Умножив это на площадь поверхности Земли, получим искомую массу атмосферы. Осталось поделить результат на массу Земли.

Дата добавления: 2019-01-14; просмотров: 203; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 5 6 7 8 91011 12 13 14 Следующая ⇒

Мы поможем в написании ваших работ!