Основные характеристики звезд 9 страница
Таким образом, в ньютоновском поле тяготения действует своеобразная "мораль", близкая к христианской: отдавая энергию в окружающую среду, -- так сказать, делая ей "добро", -- движущееся тело само от этого становится "добрее", т.е. приобретает кинетическую энергию. Вся эта энергия, как отдаваемая, так и в результате этого приобретаемая, черпается из потенциальной энергии, выступающей, если угодно, в роли "веры," рождающей "добро".
Хотя приведенное выше доказательство совершенно верно, оно тем не менее может оставить у читателя какое-то чувство неудовлетворенности. Попробуем пояснить удивительный результат, который мы обсуждаем, -- его иногда называют вириальным парадоксом -- совсем "на пальцах". Луна движется по своей орбите со скоростью  км/с. Если бы она двигалась в сопротивляющейся среде, то стала бы медленно "падать вниз" -- это кажется очевидным. Со временем она превратилась бы в низколетящий спутник, а скорость его движения, как все знают, близка к 8 км/с. Таким образом, кинетическая энергия многократно возросла бы -- и это почему-то никого не удивляет! По сути же дела это в точности то же самое, что мы обсуждали выше.
км/с. Если бы она двигалась в сопротивляющейся среде, то стала бы медленно "падать вниз" -- это кажется очевидным. Со временем она превратилась бы в низколетящий спутник, а скорость его движения, как все знают, близка к 8 км/с. Таким образом, кинетическая энергия многократно возросла бы -- и это почему-то никого не удивляет! По сути же дела это в точности то же самое, что мы обсуждали выше.
 5.15 Поскольку в условии задачи употреблено сослагательное наклонение, это означает, что на самом деле путь Луны относительно Солнца, т.е. ее орбита в Солнечной системе, точек перегиба не имеет и везде обращена выпуклостью от Солнца. Этот факт мало кто знает, и он кажется неожиданным.
5.15 Поскольку в условии задачи употреблено сослагательное наклонение, это означает, что на самом деле путь Луны относительно Солнца, т.е. ее орбита в Солнечной системе, точек перегиба не имеет и везде обращена выпуклостью от Солнца. Этот факт мало кто знает, и он кажется неожиданным.
Понятно, что кривизна траектории Луны в Солнечной системе меняется с синодическим периодом, являясь наибольшей в полнолунии и наименьшей в новолунии. Чтобы выпуклость даже в новолунии была обращена от Солнца, надо, чтобы равнодействующая сил притяжения Луны к Солнцу и к Земле была бы направлена к Солнцу. Иначе говоря, сила притяжения Луны к Солнцу 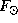 должна быть больше, чем сила ее притяжения к Земле
должна быть больше, чем сила ее притяжения к Земле 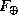 . Мы имеем:
. Мы имеем:
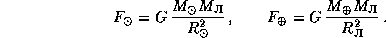
Отсюда
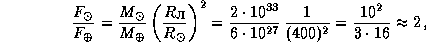
так что Луна притягивается к Солнцу примерно вдвое сильнее, чем к Земле. Не правда ли, любопытный факт?
Чтобы на лунной орбите в Солнечной системе были бы точки перегиба, в новолунии должно быть 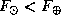 , так что расстояние до Луны должно было бы быть
, так что расстояние до Луны должно было бы быть 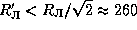 тыс. км (множитель
тыс. км (множитель 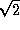 здесь не точный, он взят из полученной выше оценки значения
здесь не точный, он взят из полученной выше оценки значения 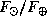 в "реальной" Солнечной системе).
в "реальной" Солнечной системе).
См. также задачу  .
.
 5.16 В курсе общей астрономии обсуждают океанские приливы, вызываемые притяжением Луны (и Солнца). Однако если сила тяжести существенно меняется на расстояниях
5.16 В курсе общей астрономии обсуждают океанские приливы, вызываемые притяжением Луны (и Солнца). Однако если сила тяжести существенно меняется на расстояниях  м, вполне ощутимые приливы будут возникать и в теле человека. Действительно, приливное ускорение равно
м, вполне ощутимые приливы будут возникать и в теле человека. Действительно, приливное ускорение равно

где M -- масса звезды, l -- характерный размер тела космонавта, r -- расстояние от космического аппарата до центра звезды. Если вы не помните этого выражения, получите его самостоятельно, записав ускорения, сообщаемые звездой наиболее и наименее удаленной от нее точкам тела и вычислив разность этих ускорений в пренебрежении малыми величинами, начиная с квадрата l/r. Предельной будем считать перегрузку a = 2 g, где g -- ускорение силы тяжести на поверхности Земли. Тогда

откуда

Типичная масса нейтронной звезды  ; характерный размер тела человека l = 100;
; характерный размер тела человека l = 100; 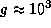 (система СГС). Отсюда
(система СГС). Отсюда 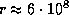 см
см  км.
км.
Поскольку радиус Солнца на два порядка больше этой величины, ясно, что при подлете к Солнцу космонавту угрожали бы совсем не приливные силы. Опасными факторами будут высокая температура, жесткое излучение и т.п.
 5.17 На первый взгляд, должно выполняться следующее условие: сила притяжения спутника к астероиду должна превосходить силу притяжения его к Солнцу. Условие равенства двух сил записывается в виде
5.17 На первый взгляд, должно выполняться следующее условие: сила притяжения спутника к астероиду должна превосходить силу притяжения его к Солнцу. Условие равенства двух сил записывается в виде
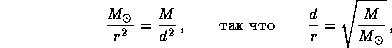
где M -- масса астероида, r -- гелиоцентрическое расстояние астероида, d -- искомое расстояние между астероидом и его спутником. Масса 100-километрового астероида (при плотности 2 г/см3) составляет 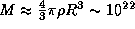 г. Поэтому
г. Поэтому  . Полагая r = 3 а.е.
. Полагая r = 3 а.е. 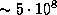 км, находим
км, находим 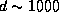 км.
км.
Однако если те же рассуждения применить не к спутнику астероида, а к спутнику Земли, максимальное расстояние окажется равным 260000 км (см. задачу  ). Луна находится на значительно большем расстоянии! Парадокс легко разрешается: на самом деле надо рассматривать не ускорение, сообщаемое спутнику Солнцем, а разность ускорений, сообщаемых спутнику и телу, вокруг которого он движется. Эта разность, как легко показать, не превосходит величины
). Луна находится на значительно большем расстоянии! Парадокс легко разрешается: на самом деле надо рассматривать не ускорение, сообщаемое спутнику Солнцем, а разность ускорений, сообщаемых спутнику и телу, вокруг которого он движется. Эта разность, как легко показать, не превосходит величины 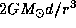 (ср. решение предыдущей задачи), и потому уравнение для определения d имеет вид
(ср. решение предыдущей задачи), и потому уравнение для определения d имеет вид

откуда

С теми же числовыми значениями получаем для нашего двойного астероида  км.
км.
Вам, может быть, интересно будет знать, каков же на самом деле минимальный радиус круговой орбиты спутника, при котором он может покинуть астероид и начать двигаться по гелиоцентрической орбите. Его определение -- это непростая задача даже для профессионалов - небесных механиков. Соответствующий радиус 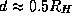 , где
, где

называется радиусом Хилла. Как видно, наша оценка совсем неплоха.
|
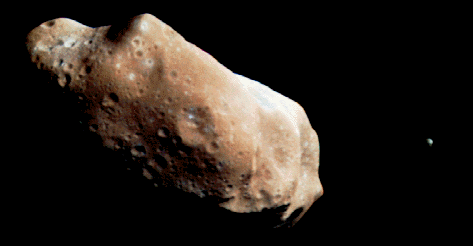
| Ида и ее спутник Дактил |
А теперь -- от сухой теории к живой сегодняшней астрономии. Космический зонд "Галилей" на своем пути к Юпитеру испытал сближение с астероидом Ида и передал его изображение. Неожиданно обнаружилось, что у Иды есть миниатюрный спутник. Изображение Иды с ее спутником см. также в Интернете по адресу http://galileo.ivv.nasa.gov/idamoon.html
 5.18 Обозначим через
5.18 Обозначим через 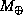 и
и  массы Земли и Солнца, через a -- расстояние между ними. Введем систему координат, как показано на рисунке внизу.
массы Земли и Солнца, через a -- расстояние между ними. Введем систему координат, как показано на рисунке внизу.
Ясно, что искомая поверхность обладает осевой симметрией относительно оси абсцисс. Поэтому достаточно найти сечение поверхности плоскостью XY, т.е. уравнение плоской кривой вида f(x,y)=0.

Записывая условие равенства сил притяжения к Солнцу и к Земле

и учитывая, что
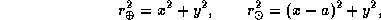
после несложных преобразований получаем уравнение сферы тяготения:
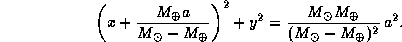
Таким образом, сфера тяготения -- это действительно сфера. Ее радиус равен
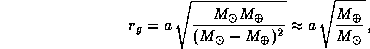
а центр смещен по оси x от центра Земли в противосолнечном направлении на расстояние
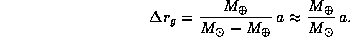
Численно, 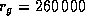 км. Орбита Луны лежит на существенно большем расстоянии, так что Солнце притягивает Луну сильнее, чем Земля -- известный парадокс,
км. Орбита Луны лежит на существенно большем расстоянии, так что Солнце притягивает Луну сильнее, чем Земля -- известный парадокс,
см. задачи  и
и  . Далее,
. Далее, 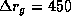 км, так что центр сферы лежит внутри Земли.
км, так что центр сферы лежит внутри Земли.
Плоскостью (проходящей точно посередине между Землей и Солнцем и перпендикулярной к линии Земля -- Солнце) сфера тяготения была бы, если бы масса Земли равнялась солнечной.
 5.19 В задаче имеются две очевидные размерные величины, R и M. Третьей, фигурирующей в задаче неявно, размерной величиной, которая также должна входить в решение, является постоянная тяготения G -- ведь движение происходит в ньютоновском гравитационном поле. Из этих трех величин "сконструировать" величину с размерностью времени проще всего так.
5.19 В задаче имеются две очевидные размерные величины, R и M. Третьей, фигурирующей в задаче неявно, размерной величиной, которая также должна входить в решение, является постоянная тяготения G -- ведь движение происходит в ньютоновском гравитационном поле. Из этих трех величин "сконструировать" величину с размерностью времени проще всего так.
Условимся через [Q] обозначать размерность величины Q. Размерность постоянной тяготения G найдем, воспользовавшись законом всемирного тяготения  , откуда [сила]=[G]г2/см2, или, так как [сила]=[масса]
, откуда [сила]=[G]г2/см2, или, так как [сила]=[масса]  [ускорение], то
[ускорение], то

Теперь ясно, что  . Поэтому, обозначив через
. Поэтому, обозначив через 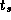 искомое время свободного падения до поверхности тела (индекс s -- от surface), мы найдем, что величина
искомое время свободного падения до поверхности тела (индекс s -- от surface), мы найдем, что величина

является безразмерной. Природа устроена так, что безразмерные комбинации определяющих параметров обычно являются числами порядка единицы. Неопределенное слово "обычно" означает здесь, что мы не находимся "рядом" с сингулярностью того или иного рода. Вероятно, эти слова покажутся читателю не вполне вразумительными -- но их полезно запомнить. Со временем вы научитесь чувствовать, что они значат.
Итак, первая (более легкая) часть задачи решена. Переходим ко второй части -- получению оценки  . По закону сохранения энергии, у падающей материальной точки единичной массы ("камня") сумма ее кинетической
. По закону сохранения энергии, у падающей материальной точки единичной массы ("камня") сумма ее кинетической 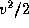 и (отрицательной) потенциальной энергии -GM/r должна оставаться постоянной. Значение этой постоянной найдем, заметив, что в начальный момент камень покоится, а потому его кинетическая энергия равна нулю, потенциальная же равна -GM/(2R). Поэтому
и (отрицательной) потенциальной энергии -GM/r должна оставаться постоянной. Значение этой постоянной найдем, заметив, что в начальный момент камень покоится, а потому его кинетическая энергия равна нулю, потенциальная же равна -GM/(2R). Поэтому

В момент падения на поверхность, т.е. при r=R, скорость камня оказывается равной

Такую же скорость имеет спутник, летящий по круговой орбите непосредственно над поверхностью планеты (первая космическая, или круговая скорость).
Чтобы оценить время свободного падения, поступим следующим образом. Представим себе, что наш "камень" падает с расстояния 2R не на планету массы M и радиуса R, а на притягивающий центр, в котором сосредоточена точечная масса M. Тогда падение камня на этот центр можно рассматривать как вырожденный случай движения по эллипсу (с эксцентриситетом e=1 и полуосью a=R). Удвоенное время падения есть период полного оборота по такой прямолинейной орбите. По третьему закону Кеплера, он равен периоду оборота спутника, движущегося по круговой орбите на расстоянии r=R от притягивающего центра -- полуоси у двух орбит одинаковы. Отсюда находим, что время падения на центр 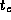 (индекс c -- от center) с расстояния 2R равно
(индекс c -- от center) с расстояния 2R равно

Ясно, что 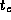 больше искомого времени падения
больше искомого времени падения 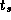 до поверхности планеты, но ненамного, так как вторую половину пути камень пролетает, принимая "промежуточный старт" при r=R с большой начальной скоростью
до поверхности планеты, но ненамного, так как вторую половину пути камень пролетает, принимая "промежуточный старт" при r=R с большой начальной скоростью  , а не с нулевой, как в начале движения с r=2R. Поэтому, оценивая время прохождения второй половины пути, мы ищем малую поправку, которую надо вычесть из
, а не с нулевой, как в начале движения с r=2R. Поэтому, оценивая время прохождения второй половины пути, мы ищем малую поправку, которую надо вычесть из 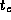 для получения
для получения 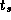 . Даже найдя эту поправку не очень точно, мы получим неплохую оценку величины
. Даже найдя эту поправку не очень точно, мы получим неплохую оценку величины 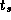 .
.
Допустим на время, что с расстояния R падение на притягивающий центр происходит с постоянным ускорением

и начальной скоростью  . На самом деле при падении на притягивающий центр ускорение растет со временем, и поэтому истинная скорость будет выше, чем при равноускоренном движении, а значит, время падения меньше. Отсюда и будет следовать оценка
. На самом деле при падении на притягивающий центр ускорение растет со временем, и поэтому истинная скорость будет выше, чем при равноускоренном движении, а значит, время падения меньше. Отсюда и будет следовать оценка  . Путь R в равноускоренном движении с ускорением
. Путь R в равноускоренном движении с ускорением  и начальной скоростью
и начальной скоростью  проходится за время
проходится за время 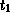 такое, что
такое, что

Из этого квадратного уравнения можем найти 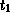 . Будем действовать не в лоб, а попробуем на нашем очень простом примере показать, что значит вести расчеты грамотно.
. Будем действовать не в лоб, а попробуем на нашем очень простом примере показать, что значит вести расчеты грамотно.
Вспомним те соображения о размерностях, с которых мы начинали решение задачи. Они подсказывают целесообразность введения вместо размерного времени t безразмерной переменной  такой, что
такой, что

Верхнему пределу изменения  , т.е.
, т.е.  , соответствует
, соответствует  . Введем также безразмерное расстояние
. Введем также безразмерное расстояние

В этих естественных для рассматриваемой задачи безразмерных переменных квадратное уравнение для нахождения 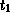 принимает вид
принимает вид

где 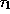 -- безразмерное время
-- безразмерное время  , соответствующее
, соответствующее 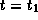 . Из этого уравнения находим, что
. Из этого уравнения находим, что

Второй корень не подходит -- он отрицателен, а время у нас отсчитывается от начала движения и потому отрицательным быть не может. Обозначим истинное безразмерное время прохождения второй половины пути камнем, падающим с r=2R, через 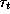 (индекс t -- от true). Ясно, что
(индекс t -- от true). Ясно, что  , а потому для безразмерного времени падения камня с r=2R до r=R, которое в условии задачи было обозначено через
, а потому для безразмерного времени падения камня с r=2R до r=R, которое в условии задачи было обозначено через  , находим
, находим

Это даже несколько более сильная оценка, чем нам требовалось получить  .
.
Дата добавления: 2019-01-14; просмотров: 152; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
