Основные характеристики звезд 13 страница
Не удивил ли вас полученный результат? Как вы думаете, почему же мы не видим Европу простым глазом?
 7.13 Действительно,
7.13 Действительно,
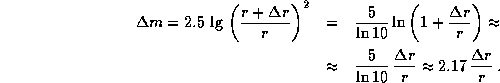
Здесь мы воспользовались приближенным равенством 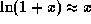 , справедливым при
, справедливым при 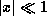 , что следует из замечательного предела
, что следует из замечательного предела

Полученная нами формула, связывающая 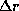 и
и 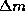 , очень полезна. Ее нет ни в одном известном авторам учебнике астрономии, о чем можно только пожалеть.
, очень полезна. Ее нет ни в одном известном авторам учебнике астрономии, о чем можно только пожалеть.
К планетам эту формулу применять нельзя, точнее, можно применять не всегда (почему?).
 7.14 Блеск планеты (орбиту которой мы считаем, естественно, круговой) меняется из-за изменения ее геоцентрического расстояния. Отношение расстояний в противостоянии и в соединении есть
7.14 Блеск планеты (орбиту которой мы считаем, естественно, круговой) меняется из-за изменения ее геоцентрического расстояния. Отношение расстояний в противостоянии и в соединении есть
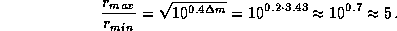
[То, что 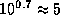 , находим в уме, учтя, что
, находим в уме, учтя, что 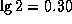 ]. Но для внешней планеты (у нижних не бывает противостояний!)
]. Но для внешней планеты (у нижних не бывает противостояний!)
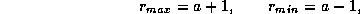
где радиус орбиты планеты выражен в а.е. Поэтому

откуда a = 1.5. Это -- Марс.
Впрочем, надеемся, что вы сразу же это сообразили без всякого расчета, едва прочли условие задачи. Всякий, кто интересуется астрономией и хоть немного следил за небом, знает, что ни Юпитер, ни тем более Сатурн так сильно, почти на три с половиной звездных величины, своего блеска не меняют. Расчет подтвердил эту правильную догадку.
 7.15 Рассуждая, как в задаче
7.15 Рассуждая, как в задаче  , легко найдем, что большая полуось планеты составляет 5.2 а.е., так что эта планета -- Юпитер. Другой, более простой способ убедиться в этом -- воспользоваться соотношением из задачи
, легко найдем, что большая полуось планеты составляет 5.2 а.е., так что эта планета -- Юпитер. Другой, более простой способ убедиться в этом -- воспользоваться соотношением из задачи  , взяв в нем
, взяв в нем 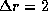 , что дает
, что дает 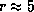 -- сразу опознается Юпитер.
-- сразу опознается Юпитер.
|
|
|
Сидерический период обращения Юпитера вокруг Солнца P равен приблизительно 12 годам. Синодический период S найдем из уравнения синодического движения

где T -- сидерический период обращения Земли. Синодический период Юпитера в годах равен, таким образом, 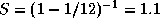 года, а промежуток времени от соединения до противостояния -- половина синодического периода, т.е. около шести с половиной месяцев.
года, а промежуток времени от соединения до противостояния -- половина синодического периода, т.е. около шести с половиной месяцев.
 7.16 Грубая оценка получается мгновенно. Абсолютная звездная величина Солнца примерно +5m, так что с расстояния в 10 парсеков Солнце будет видно как звезда пятой величины. Предельное расстояние, с которого Солнце еще можно увидеть глазом, должно быть немного больше этого. По формуле из задачи
7.16 Грубая оценка получается мгновенно. Абсолютная звездная величина Солнца примерно +5m, так что с расстояния в 10 парсеков Солнце будет видно как звезда пятой величины. Предельное расстояние, с которого Солнце еще можно увидеть глазом, должно быть немного больше этого. По формуле из задачи  легко найдем (по-прежнему считая абсолютную звездную величину Солнца равной +5m), что еще на одну звездную величину слабее Солнце станет, если удалиться от него еще на
легко найдем (по-прежнему считая абсолютную звездную величину Солнца равной +5m), что еще на одну звездную величину слабее Солнце станет, если удалиться от него еще на 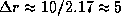 пк. Итак, искомое расстояние близко к 15 пк.
пк. Итак, искомое расстояние близко к 15 пк.
Вот более аккуратный расчет. Абсолютная звездная величина Солнца (в полосе V) равна 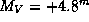 . Невооруженным глазом видны звезды до 6-й звездной величины. Из известной формулы, связывающей M, m и r, находим
. Невооруженным глазом видны звезды до 6-й звездной величины. Из известной формулы, связывающей M, m и r, находим
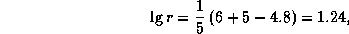
откуда r = 17 пк.
 7.17 Как известно,
7.17 Как известно,  Cen -- звезда, по своим физическим характеристикам очень похожая на Солнце. Поэтому можно с уверенностью утверждать, что для наблюдателя, живущего в окрестностях
Cen -- звезда, по своим физическим характеристикам очень похожая на Солнце. Поэтому можно с уверенностью утверждать, что для наблюдателя, живущего в окрестностях  Cen, Солнце определенно будет в числе самых ярких звезд -- ведь
Cen, Солнце определенно будет в числе самых ярких звезд -- ведь  Cen входит в число таких звезд для земного наблюдателя. При этом следует также учесть, что
Cen входит в число таких звезд для земного наблюдателя. При этом следует также учесть, что  Cen -- ближайшая к Солнцу звезда, а все остальные яркие звезды находятся в несколько раз дальше и от Солнца, и от
Cen -- ближайшая к Солнцу звезда, а все остальные яркие звезды находятся в несколько раз дальше и от Солнца, и от  Cen.
Cen.
|
|
|
 7.18 Абсолютная визуальная звездная величина Солнца -- около +5m. Отсюда
7.18 Абсолютная визуальная звездная величина Солнца -- около +5m. Отсюда
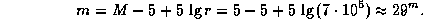
Таким образом, при наблюдении из туманности Андромеды (если не помешает межзвездная пыль) Солнце имело бы звездную величину, примерно равную 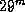 . Оно было бы недоступно крупнейшим наземным телескопам (
. Оно было бы недоступно крупнейшим наземным телескопам ( 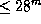 ), но теоретически находилось бы на пределе обнаружимости для хаббловского космического телескопа. Практически же увидеть Солнце было бы невозможно, так как его излучение сливалось бы со светом от тысяч соседних с ним звезд.
), но теоретически находилось бы на пределе обнаружимости для хаббловского космического телескопа. Практически же увидеть Солнце было бы невозможно, так как его излучение сливалось бы со светом от тысяч соседних с ним звезд.
 7.19 Абсолютная болометрическая звездная величина -- это мера мощности. Пусть M -- искомая абсолютная болометрическая звездная величина пылесоса, а L -- его мощность, которую мы примем равной 800 Вт. Те же величины для Солнца равны
7.19 Абсолютная болометрическая звездная величина -- это мера мощности. Пусть M -- искомая абсолютная болометрическая звездная величина пылесоса, а L -- его мощность, которую мы примем равной 800 Вт. Те же величины для Солнца равны 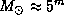 и
и 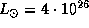 Вт. Тогда
Вт. Тогда
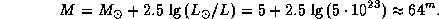
Слабый источник -- пылесос...
Излучение
 8.1 Функция Планка в шкале длин волн имеет вид
8.1 Функция Планка в шкале длин волн имеет вид
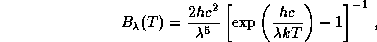
а приближение Вина дается формулой
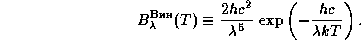
Поэтому
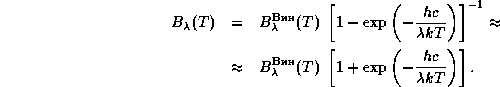
Значит, относительная погрешность приближения Вина 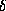 =
= 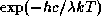 . С другой стороны, исследуя функцию Вина на максимум, легко найти, что
. С другой стороны, исследуя функцию Вина на максимум, легко найти, что

Этот очень полезный результат есть закон смещения Вина. Обычно ограничиваются тем, что отмечают постоянство произведения 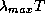 . Однако очень важно и численное значение
. Однако очень важно и численное значение 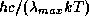 , точнее, то, что это число заметно превосходит 1. Действительно, мы имеем
, точнее, то, что это число заметно превосходит 1. Действительно, мы имеем 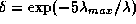 , так что
, так что 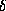 мало при
мало при 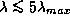 . Интенсивность в максимуме, которую мы (теперь обоснованно) вычисляем в приближении Вина, есть
. Интенсивность в максимуме, которую мы (теперь обоснованно) вычисляем в приближении Вина, есть
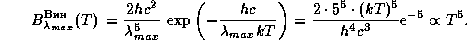
|
|
|
Если не пользоваться приближением Вина, а работать с точной планковской функцией, то оказывается, что 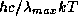 равно не точно 5, а 4.965 (проверьте!). Все остальное, включая заключение, что
равно не точно 5, а 4.965 (проверьте!). Все остальное, включая заключение, что 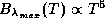 , остается в силе.
, остается в силе.
Длинноволновое приближение Рэлея-Джинса, противоположное приближению Вина, обеспечивает относительную погрешность 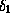 лишь при
лишь при 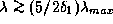 (проверьте). Скажем, точность в 10% приближение Рэлея-Джинса дает лишь при
(проверьте). Скажем, точность в 10% приближение Рэлея-Джинса дает лишь при 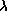 , превосходящих
, превосходящих 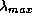 в 25 раз!
в 25 раз!
В итоге оказывается, что вся планковская кривая 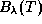 , как ее видит глаз на обычном графике, неотличима от виновской кривой. Большинство же студентов (да, пожалуй, и экс-студентов тоже) ошибочно полагает, что приближение Вина для
, как ее видит глаз на обычном графике, неотличима от виновской кривой. Большинство же студентов (да, пожалуй, и экс-студентов тоже) ошибочно полагает, что приближение Вина для 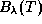 применимо только слева от максимума, приближение Рэлея-Джинса начинает работать слегка правее него, а сам максимум хорошо описывается лишь точной формулой Планка. На самом деле, как мы убедились, все совсем не так.
применимо только слева от максимума, приближение Рэлея-Джинса начинает работать слегка правее него, а сам максимум хорошо описывается лишь точной формулой Планка. На самом деле, как мы убедились, все совсем не так.
|
|
|
 8.2 Планковские кривые, соответствующие разным T, не пересекаются, поскольку
8.2 Планковские кривые, соответствующие разным T, не пересекаются, поскольку 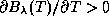 . Отсюда следует, что при любом (фиксированном)
. Отсюда следует, что при любом (фиксированном) 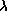 значения
значения 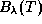 монотонно возрастают с T. Далее, высота максимума планковской кривой, т.е. максимальное значение интенсивности, пропорциональна
монотонно возрастают с T. Далее, высота максимума планковской кривой, т.е. максимальное значение интенсивности, пропорциональна 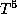 для
для 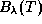 и
и 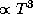 для
для 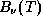 . Это легко показать, исследуя на максимум соответствующие функции Планка (см. задачу
. Это легко показать, исследуя на максимум соответствующие функции Планка (см. задачу  ). Площадь же под обеими кривыми, и
). Площадь же под обеими кривыми, и 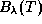 и
и 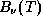 , растет
, растет 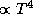 (закон Стефана-Больцмана). Поэтому с ростом температуры кривая Планка в шкале длин волн "заостряется", а в шкале частот -- "притупляется".
(закон Стефана-Больцмана). Поэтому с ростом температуры кривая Планка в шкале длин волн "заостряется", а в шкале частот -- "притупляется".
 8.3 Пусть f(x) дифференцируема в точке
8.3 Пусть f(x) дифференцируема в точке 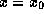 . Для простоты считаем, что
. Для простоты считаем, что 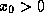 и
и 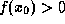 . Для получения степенной аппроксимации f(x) в окрестности
. Для получения степенной аппроксимации f(x) в окрестности 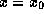 , т.е. представления f(x) вида
, т.е. представления f(x) вида
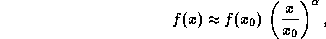
поступим следующим образом. Будем рассматривать 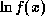 как функцию
как функцию 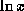 . Тогда имеем обычную линеаризацию в окрестности
. Тогда имеем обычную линеаризацию в окрестности 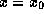 :
:
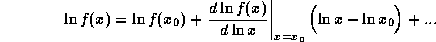
Отсюда, потенцируя, получаем вышеприведенную степенную аппроксимацию f(x), причем обнаруживается, что
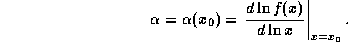
Подобные степенные аппроксимации используются в физике (и, в частности, в астрофизике) буквально на каждом шагу. К сожалению, ни в одном известном авторам курсе математического анализа об этом нет ни слова -- хотя учить этому следовало бы всех, даже изучающих анализ не слишком глубоко. Видимо, считается, что студент сам все это сообразит, когда немного "подрастет". Мы решили нарушить традицию и не ждать, когда это случится.
Приведенная в условии задачи степенная аппроксимация зависимости чернотельной интенсивности 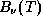 от T в окрестности
от T в окрестности 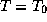 получается только что описанным стандартным способом. Выкладку предоставляем читателю.
получается только что описанным стандартным способом. Выкладку предоставляем читателю.
Степенная аппроксимация функции Планка, которую почему-то не отыщешь ни в одном учебнике, позволяет понять многие качественные особенности солнечного и звездных спектров. См., в частности, задачу  .
.
 8.4 А почему, собственно, она должна равняться (3/2)kT? Ведь фотон -- не классическая частица, движущаяся с нерелятивистской скоростью. А только к таким частицам и применима классическая формула (3/2)kT.
8.4 А почему, собственно, она должна равняться (3/2)kT? Ведь фотон -- не классическая частица, движущаяся с нерелятивистской скоростью. А только к таким частицам и применима классическая формула (3/2)kT.
Чтобы найти среднюю энергию одного чернотельного фотона 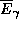 , надо объемную плотность энергии поля излучения
, надо объемную плотность энергии поля излучения
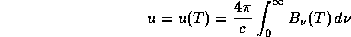
поделить на число фотонов в единице объема
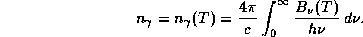
Сделав в обоих интегралах одну и ту же замену 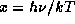 , обнаруживаем, что
, обнаруживаем, что

где
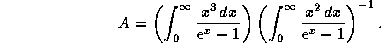
Для оценки A можно воспользоваться приближением Вина, т.е. пренебречь 1 по сравнению с 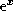 в двух последних интегралах (ср. с обсуждением в задаче
в двух последних интегралах (ср. с обсуждением в задаче  ). Тогда немедленно получим, что
). Тогда немедленно получим, что 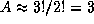 , поскольку (советуем это запомнить)
, поскольку (советуем это запомнить)
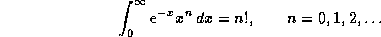
Последнее легко доказывается интегрированием по частям. Итак, 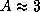 ; вычислив интегралы точно, мы нашли бы, что A=2.70, так что окончательно
; вычислив интегралы точно, мы нашли бы, что A=2.70, так что окончательно

Таким образом, средняя энергия одного чернотельного фотона без малого вдвое больше средней энергии теплового движения нерелятивистской частицы. Однако вклад каждого фотона в давление почти в точности такой же, как и каждой частицы: давление излучения 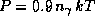 , газовое же давление P = n k T, где
, газовое же давление P = n k T, где 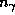 и n -- концентрации фотонов и частиц, соответственно. (Как вы думаете, почему так получается? Впрочем, это уже скорее физика, чем астрономия. Но ведь решаемся же мы нет-нет да и приучить вас к "физической математике", так почему же не поучить чуть-чуть и "астрономической физике"?) Из только что сказанного следует, что отношение концентраций фотонов и частиц есть одновременно (с точностью
и n -- концентрации фотонов и частиц, соответственно. (Как вы думаете, почему так получается? Впрочем, это уже скорее физика, чем астрономия. Но ведь решаемся же мы нет-нет да и приучить вас к "физической математике", так почему же не поучить чуть-чуть и "астрономической физике"?) Из только что сказанного следует, что отношение концентраций фотонов и частиц есть одновременно (с точностью 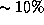 ) и отношение давления излучения к газовому (см. задачу
) и отношение давления излучения к газовому (см. задачу  ).
).
 8.5 Выражение для
8.5 Выражение для 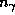 уже появлялось в решении предыдущей задачи:
уже появлялось в решении предыдущей задачи:
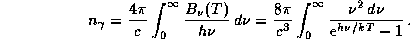
Подстановка 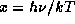 приводит его к виду
приводит его к виду
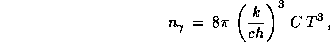
где

Таким образом, 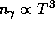 . Чтобы найти точное значение коэффициента пропорциональности, надо получить C. Как мы знаем (см. решение предыдущей задачи), приближенно можно считать, что C=2. Точное же значение C получается так:
. Чтобы найти точное значение коэффициента пропорциональности, надо получить C. Как мы знаем (см. решение предыдущей задачи), приближенно можно считать, что C=2. Точное же значение C получается так:
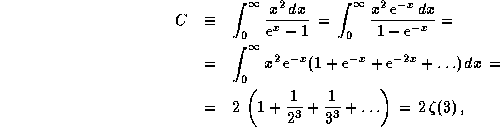
где 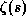 -- дзета-функция Римана:
-- дзета-функция Римана:
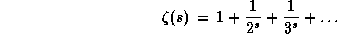
Число 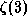 не выражается через какие-либо "стандартные" постоянные (
не выражается через какие-либо "стандартные" постоянные (  , e, постоянную Эйлера и т.п.). Оно равно
, e, постоянную Эйлера и т.п.). Оно равно 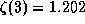 .
.
Дата добавления: 2019-01-14; просмотров: 174; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
