Основные характеристики звезд 14 страница
После подстановки всех постоянных в полученное выше выражение для 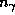 находим, что
находим, что

Мы несколько отступили здесь от нашего обычного стиля -- получать скорее оценки, чем точные результаты, и стараться избегать громоздких расчетов. Сделать это хотя бы один раз, однако, полезно.
А вот как формулу  можно получить совсем просто, комбинируя другие известные результаты. Плотность лучистой энергии равновесного излучения равна
можно получить совсем просто, комбинируя другие известные результаты. Плотность лучистой энергии равновесного излучения равна

где a -- постоянная плотности излучения:

а средняя энергия одного фотона  (см. предыдущую задачу). Поэтому
(см. предыдущую задачу). Поэтому
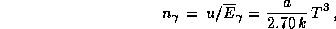
что сразу же и дает коэффициент 20 при  . На самом деле, конечно, ничего принципиально нового в таком способе расчета нет -- просто мы использовали готовое численное значение постоянной плотности излучения a (оно есть, например, у Аллена [1]).
. На самом деле, конечно, ничего принципиально нового в таком способе расчета нет -- просто мы использовали готовое численное значение постоянной плотности излучения a (оно есть, например, у Аллена [1]).
 8.6 Частота фотона, испускаемого при переходе атома водорода с уровня m на уровень n, дается известной формулой
8.6 Частота фотона, испускаемого при переходе атома водорода с уровня m на уровень n, дается известной формулой

где  -- частота предела ионизации с первого уровня,
-- частота предела ионизации с первого уровня,  Гц.
Гц.
Перейдем от частот к длинам волн:

где 
 .
.
Искомый переход найдем перебором. Вначале положим n=1. Тогда для m=2 получаем 
 . Это знаменитая линия лайман-альфа, или
. Это знаменитая линия лайман-альфа, или  . Ясно, что для m>2 будем иметь
. Ясно, что для m>2 будем иметь 
 , т.е. переходы на первый уровень нам не подходят. Возьмем n=2. Тогда для m=3 получим
, т.е. переходы на первый уровень нам не подходят. Возьмем n=2. Тогда для m=3 получим 
 . Это и есть искомый переход (линия H
. Это и есть искомый переход (линия H  ). Различие в длине волны в четвертом знаке (6 вместо 3) нас смущать не должно, так как при расчете мы использовали значение
). Различие в длине волны в четвертом знаке (6 вместо 3) нас смущать не должно, так как при расчете мы использовали значение  лишь с тремя значащими цифрами.
лишь с тремя значащими цифрами.
|
|
|
 8.7 По формуле из решения предыдущей задачи находим
8.7 По формуле из решения предыдущей задачи находим

Таким образом, линия межзвездного водорода H 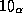 лежит в субмиллиметровом диапазоне. Излучение в нем поглощается земной атмосферой. Наземные наблюдения линии невозможны.
лежит в субмиллиметровом диапазоне. Излучение в нем поглощается земной атмосферой. Наземные наблюдения линии невозможны.
 8.8 Линия H
8.8 Линия H  возникает при переходе
возникает при переходе  в атоме водорода. Из общей сериальной формулы для водорода (см. задачу
в атоме водорода. Из общей сериальной формулы для водорода (см. задачу  )
)

полагая m=n+1 и считая, что 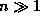 , находим
, находим

Согласно этой формуле, линия H  , например, имеет длину волны около 5 см.
, например, имеет длину волны около 5 см.
Подобные радиолинии, возникающие при переходах между близкими высокорасположенными уровнями, давно уже наблюдаются в туманностях. Как вы думаете, есть ли надежда обнаружить их также в радиоизлучении Солнца? (Ср. задачу  .)
.)
 8.9 Исходим из сериальной формулы для водорода в шкале частот:
8.9 Исходим из сериальной формулы для водорода в шкале частот:

Полагая в ней  и считая, что
и считая, что 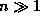 и
и  , получим
, получим

Отсюда видно, что, действительно, при увеличении  на единицу частота соответствующего перехода возрастает на одну и ту же величину
на единицу частота соответствующего перехода возрастает на одну и ту же величину  которая есть не что иное как частота линии H
которая есть не что иное как частота линии H  .
.
 8.10 Ионизация атомов водорода с n-го уровня может производиться фотонами с длиной волны короче, чем та, которую имеет излучение, образующееся при переходе атома водорода с уровня
8.10 Ионизация атомов водорода с n-го уровня может производиться фотонами с длиной волны короче, чем та, которую имеет излучение, образующееся при переходе атома водорода с уровня  на уровень n. По формуле из решения задачи
на уровень n. По формуле из решения задачи  находим, что эта длина волны равна
находим, что эта длина волны равна 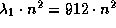
 . При n = 2 имеем 3648
. При n = 2 имеем 3648  (на самом деле 3646
(на самом деле 3646  ). Таким образом, излучение видимого диапазона не способно ионизовать атомы водорода со второго уровня. Это очень важное заключение.
). Таким образом, излучение видимого диапазона не способно ионизовать атомы водорода со второго уровня. Это очень важное заключение.
|
|
|
 8.11 Причина этого -- различие плотности. В атмосферах белых карликов она значительно выше, чем в солнечной хромосфере (почему?). Поэтому средние расстояния между атомами в хромосфере гораздо больше, чем в атмосферах белых карликов. Но радиус n-й боровской орбиты
8.11 Причина этого -- различие плотности. В атмосферах белых карликов она значительно выше, чем в солнечной хромосфере (почему?). Поэтому средние расстояния между атомами в хромосфере гораздо больше, чем в атмосферах белых карликов. Но радиус n-й боровской орбиты  быстро растет с n, именно,
быстро растет с n, именно, 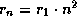 . Понятно, что он не может быть больше среднего расстояния между атомами -- иначе станет непонятно, какому именно атому принадлежит электрон, находящийся на этом уровне, т.е. произойдет его "обобществление". Поэтому, чем выше плотность, тем меньшее число уровней реализуется, а потому и тем меньшее число бальмеровских линий может возникать.
. Понятно, что он не может быть больше среднего расстояния между атомами -- иначе станет непонятно, какому именно атому принадлежит электрон, находящийся на этом уровне, т.е. произойдет его "обобществление". Поэтому, чем выше плотность, тем меньшее число уровней реализуется, а потому и тем меньшее число бальмеровских линий может возникать.
Удивительно, но факт: просто подсчитывая число бальмеровских линий, которые видны в спектре той или иной звезды, можно оценить плотность ее атмосферы!
Спектры Солнца и звезд
 9.1 Фраунгоферовы линии -- это линии поглощения в видимой части спектра Солнца (линий в других областях спектра Фраунгофера в начале 19 в. наблюдать, естественно, не мог). Наряду с другими причинами, уширение этих линий вызывается тепловым движением атомов в атмосфере Солнца. Оценим характерную тепловую скорость атомов водорода на Солнце. Из условия
9.1 Фраунгоферовы линии -- это линии поглощения в видимой части спектра Солнца (линий в других областях спектра Фраунгофера в начале 19 в. наблюдать, естественно, не мог). Наряду с другими причинами, уширение этих линий вызывается тепловым движением атомов в атмосфере Солнца. Оценим характерную тепловую скорость атомов водорода на Солнце. Из условия

находим

|
|
|
Подставляя значения  эрг/K (постоянная Больцмана), T=5800 K (температура "поверхности" Солнца) и
эрг/K (постоянная Больцмана), T=5800 K (температура "поверхности" Солнца) и  г (масса атома водорода мало отличается от массы протона), получаем
г (масса атома водорода мало отличается от массы протона), получаем  км/с. (Это число полезно помнить. Оно порядка скорости звука в атмосфере Солнца.) По формуле эффекта Доплера при такой лучевой скорости длина волны видимого света
км/с. (Это число полезно помнить. Оно порядка скорости звука в атмосфере Солнца.) По формуле эффекта Доплера при такой лучевой скорости длина волны видимого света 
 ) смещается на величину
) смещается на величину 
 . Соответствующая ширина линий порядка
. Соответствующая ширина линий порядка 
 , так как скорости частиц газа могут быть направлены как к наблюдателю, так и в противоположном направлении.
, так как скорости частиц газа могут быть направлены как к наблюдателю, так и в противоположном направлении.
Эта оценка относится к водороду. Для атома с массой m ширина линии будет в  раз меньше (почему?).
раз меньше (почему?).
Найденные нами ширины -- минимальные: тепловые скорости есть всегда. В действительности существуют и другие причины уширения. В итоге сильные линии (в частности, и бальмеровские линии водорода) оказываются значительно шире.
 9.2 Из-за вращения один край диска приближается к нам, другой удаляется. Поэтому линия, которая была бы бесконечно узкой у невращающейся звезды, оказывается уширенной -- ведь к нам приходит излучение со всего диска, а из-за вращения в разных его точках лучевая скорость, а значит, и вызванное ею доплеровское смещение различны. Если ось вращения перпендикулярна к лучу зрения, то доплеровское уширение линии, обусловленное вращением, будет составлять
9.2 Из-за вращения один край диска приближается к нам, другой удаляется. Поэтому линия, которая была бы бесконечно узкой у невращающейся звезды, оказывается уширенной -- ведь к нам приходит излучение со всего диска, а из-за вращения в разных его точках лучевая скорость, а значит, и вызванное ею доплеровское смещение различны. Если ось вращения перпендикулярна к лучу зрения, то доплеровское уширение линии, обусловленное вращением, будет составлять

(А что будет, если угол наклона оси вращения к лучу зрения не  , а i?)
, а i?)
|
|
|
Обратимся к конкретному случаю, указанному в условии задачи. Радиус звезды спектрального класса B0V можно принять равным 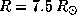 . Поэтому периоду осевого вращения
. Поэтому периоду осевого вращения  соответствует скорость вращения на экваторе
соответствует скорость вращения на экваторе  км/с. Линия с длиной волны
км/с. Линия с длиной волны 
 будет иметь
будет иметь 
 .
.
 9.3 Линии H и K Ca II -- резонансные, т.е. они возникают при переходах с основного уровня. Линии же
9.3 Линии H и K Ca II -- резонансные, т.е. они возникают при переходах с основного уровня. Линии же 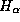 и
и  возникают при переходах с первого возбужденного уровня, отстоящего от основного на 10.2 эВ. При температуре
возникают при переходах с первого возбужденного уровня, отстоящего от основного на 10.2 эВ. При температуре 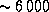 K на этом уровне находится лишь очень малая доля атомов водорода, подавляющее же большинство -- на основном уровне. Населенность i-го уровня
K на этом уровне находится лишь очень малая доля атомов водорода, подавляющее же большинство -- на основном уровне. Населенность i-го уровня  можно оценить по формуле Больцмана
можно оценить по формуле Больцмана

где  -- статистический вес i-го уровня (для водорода
-- статистический вес i-го уровня (для водорода  ) и
) и  -- энергия его возбуждения (10.2 эВ для i = 2, т.е. для первого возбужденного уровня водорода). Поскольку энергии в 1 эВ соответствует температура 11600 К, то при
-- энергия его возбуждения (10.2 эВ для i = 2, т.е. для первого возбужденного уровня водорода). Поскольку энергии в 1 эВ соответствует температура 11600 К, то при  К оказывается, что
К оказывается, что 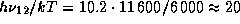 . Поэтому при
. Поэтому при  K доля атомов водорода, находящихся на втором уровне, составляет всего
K доля атомов водорода, находящихся на втором уровне, составляет всего  . Но
. Но  (напоминаем, что
(напоминаем, что 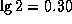 ), а
), а  , так что доля атомов на втором уровне составляет
, так что доля атомов на втором уровне составляет  . Их концентрация существенно ниже концентрации ионов кальция (содержание кальция
. Их концентрация существенно ниже концентрации ионов кальция (содержание кальция  от водорода; кальций в солнечной атмосфере сильно ионизован, так как энергия его ионизации сравнительно невелика,
от водорода; кальций в солнечной атмосфере сильно ионизован, так как энергия его ионизации сравнительно невелика,  эВ). В итоге резонансные линии иона кальция оказываются сильнее бальмеровских линий.
эВ). В итоге резонансные линии иона кальция оказываются сильнее бальмеровских линий.
 9.4 Чтобы ответить на поставленные вопросы, следует прежде всего понять, почему есть бальмеровский скачок. Поглощение излучения в атмосферах с температурой
9.4 Чтобы ответить на поставленные вопросы, следует прежде всего понять, почему есть бальмеровский скачок. Поглощение излучения в атмосферах с температурой  K вызывается нейтральным водородом. По коротковолновую сторону от бальмеровского предела при
K вызывается нейтральным водородом. По коротковолновую сторону от бальмеровского предела при 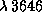
 \ (скажем, на
\ (скажем, на 
 ) излучение способно ионизовать атомы водорода со всех уровней, начиная со второго, по длинноволновую сторону от этого предела (скажем, на
) излучение способно ионизовать атомы водорода со всех уровней, начиная со второго, по длинноволновую сторону от этого предела (скажем, на 
 ) фотоны могут ионизовать водород лишь с третьего и более высоких уровней. В результате на
) фотоны могут ионизовать водород лишь с третьего и более высоких уровней. В результате на 
 \ атмосфера оказывается более прозрачной, и мы видим более глубокие и потому более горячие ее слои. Излучение их сильное. По коротковолновую сторону от предела (на
\ атмосфера оказывается более прозрачной, и мы видим более глубокие и потому более горячие ее слои. Излучение их сильное. По коротковолновую сторону от предела (на 
 ) непрозрачность газа велика, излучение приходит лишь из самых поверхностных, а значит, более холодных слоев, и потому оно слабее.
) непрозрачность газа велика, излучение приходит лишь из самых поверхностных, а значит, более холодных слоев, и потому оно слабее.
Теперь уже легко ответить и на вопрос о потемнении. Там, где непрозрачность велика ( 
 ), во всех точках диска излучение приходит почти из одних и тех же, самых поверхностных слоев. Поэтому потемнение к краю должно быть мало. С излучением по длинноволновую сторону от предела (
), во всех точках диска излучение приходит почти из одних и тех же, самых поверхностных слоев. Поэтому потемнение к краю должно быть мало. С излучением по длинноволновую сторону от предела ( 
 ) положение другое. В центре диска оно приходит со сравнительно большой глубины, где горячо, а на краю луч зрения скользит по атмосферным слоям, и излучение приходит только из самых наружных холодных слоев. Значит, на этих длинах волн должно быть значительное потемнение.
) положение другое. В центре диска оно приходит со сравнительно большой глубины, где горячо, а на краю луч зрения скользит по атмосферным слоям, и излучение приходит только из самых наружных холодных слоев. Значит, на этих длинах волн должно быть значительное потемнение.
Можно утверждать, что отношение яркостей в центре и на краю по длинноволновую сторону от предела заведомо больше, чем величина наблюдаемого в спектре звезды скачка (поймите, почему).
 9.5 Мы настолько привыкли к тому, что излучение Солнца в первом приближении можно считать чернотельным, что обычно не задаемся вопросом, почему, собственно, это так. Между тем вопрос нетривиален. Действительно, если бы температура Солнца была не 6000 K, а 10000 K, то оно было бы звездой класса A0V, и спектр был бы совсем не похож на планковский -- имелся бы большой бальмеровский скачок на
9.5 Мы настолько привыкли к тому, что излучение Солнца в первом приближении можно считать чернотельным, что обычно не задаемся вопросом, почему, собственно, это так. Между тем вопрос нетривиален. Действительно, если бы температура Солнца была не 6000 K, а 10000 K, то оно было бы звездой класса A0V, и спектр был бы совсем не похож на планковский -- имелся бы большой бальмеровский скачок на 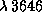
 и т. д. Так почему же распределение энергии в спектре Солнца похоже на планковское? По сути дела, причина этого в том, что атмосфера Солнца почти серая, т.е. ослабляет проходящее через нее излучение неселективно. Это вызвано тем, что основным источником непрозрачности газа в солнечной атмосфере является не нейтральный водород, как у звезд класса A (последний поглощает излучение разных длин волн весьма по-разному -- отсюда, в частности, и бальмеровский скачок, см. предыдущую задачу), а отрицательный ион водорода (см. задачу
и т. д. Так почему же распределение энергии в спектре Солнца похоже на планковское? По сути дела, причина этого в том, что атмосфера Солнца почти серая, т.е. ослабляет проходящее через нее излучение неселективно. Это вызвано тем, что основным источником непрозрачности газа в солнечной атмосфере является не нейтральный водород, как у звезд класса A (последний поглощает излучение разных длин волн весьма по-разному -- отсюда, в частности, и бальмеровский скачок, см. предыдущую задачу), а отрицательный ион водорода (см. задачу  ). Он поглощает видимое излучение всех длин волн почти одинаково. Температура в солнечной атмосфере, точнее, в тех слоях, которые мы непосредственно видим, различается не сильно и близка к 6000 K. Поэтому наблюдаемый спектр есть наложение планковских кривых со слегка различающимися температурами, входящими с весовыми множителями, учитывающими нейтральное, т.е. одинаковое для всех длин волн ослабление излучения при прохождении им слоев атмосферы, лежащих над тем уровнем, где свет был излучен. В результате и получается, что спектр Солнца близок к чернотельному с
). Он поглощает видимое излучение всех длин волн почти одинаково. Температура в солнечной атмосфере, точнее, в тех слоях, которые мы непосредственно видим, различается не сильно и близка к 6000 K. Поэтому наблюдаемый спектр есть наложение планковских кривых со слегка различающимися температурами, входящими с весовыми множителями, учитывающими нейтральное, т.е. одинаковое для всех длин волн ослабление излучения при прохождении им слоев атмосферы, лежащих над тем уровнем, где свет был излучен. В результате и получается, что спектр Солнца близок к чернотельному с  К.
К.
Дата добавления: 2019-01-14; просмотров: 185; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
