Основные характеристики звезд 6 страница

⇐ ПредыдущаяСтр 6 из 16Следующая ⇒

2.17 Для наступления хотя бы частного солнечного затмения необходимо, чтобы угловое расстояние центра диска Луны от центра диска Солнца не превосходило суммы угловых радиусов Луны и Солнца, т.е. . Поскольку центр диска Солнца движется по эклиптике, это условие можно переформулировать так: топоцентрическая эклиптическая широта Луны должна быть не более 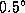. Так как горизонтальный суточный параллакс Луны составляет , а параллаксом Солнца можно пренебречь, геоцентрическая эклиптическая широта Луны должна быть не более .

Теперь рассмотрим прямоугольный сферический треугольник, вершинами которого служат центр диска Луны M, центр диска Солнца S и узел лунной орбиты (см. рис.). Сторонами треугольника являются дуги эклиптики, орбиты Луны и большого круга, проходящего через центры дисков Луны и Солнца и полюсы эклиптики. Угол при центре Солнца прямой.

Острый угол при узле лунной орбиты есть наклон орбиты к плоскости эклиптики, . Катеты треугольника равны расстоянию Солнца от узла и геоцентрической эклиптической широте Луны . Треугольник с хорошей точностью можно считать плоским и узким, так что . Но рад. Поэтому .

2.18 Задача интересна в "бытовом" смысле: любопытно, на сколько отличается от 12 часов момент наступления "настоящего" полудня -- момента, когда Солнце выше всего, тени от предметов ориентированы строго на север или на юг (куда именно -- на север или на юг -- зависит от широты места и времени года; разберитесь в этом самостоятельно) и т. д.

Для определенности предположим, что сегодня 10 ноября, и вы находитесь в Петербурге.

Истинный полдень -- момент, когда истинное солнечное время . Среднее солнечное время составит , где -- уравнение времени. Воспользовавшись графиком, дающим уравнение времени на разные даты (см., например, [2], рис. 14), найдем, что 10 ноября . Следовательно, .

Всемирное время , а долгота центра Петербурга , так что .

Следующий шаг -- вычисление поясного времени. Петербург находится во втором часовом поясе, поэтому .

Наконец, вспомним, что в России действует декретное время, которое на один час впереди поясного. Летнее время, добавляющее еще час, 1-го ноября не действует, поэтому московское время совпадает с декретным. Окончательно получаем

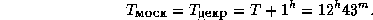
2.19 Так как солнечное время отсчитывается от полуночи, то когда в Гринвиче 0 ^h, там полночь, т.е. Солнце -- в нижней кульминации. В верхней же кульминации оно будет в этот момент на противоположной стороне земного шара, так что долгота места наблюдения равна 12 ^h.

2.20 a) Период колебаний маятника длиной l дается формулой Гюйгенса

где -- ускорение свободного падения, G -- гравитационная постоянная, M -- масса Земли, R -- расстояние от центра Земли в точке, где находится маятник. Таким образом,

так что

откуда

От экватора к полюсу , и значит, 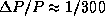. За сутки часы уйдут на .

б) Изменение периода, обусловленное изменением l, приближенно равно

Поэтому требуемое для компенсации изменения хода часов изменение длины маятника

При длине маятника 1.5 м на полюсе его следует удлинить на 1 см.

2.21 Ответ поразителен: часы уйдут на целый час! Действительно, Земля вращается равноускоренно (точнее, равнозамедленно). Пусть -- ее начальная угловая скорость, -- угловое ускорение, -- угловая скорость в момент t. Тогда

Но

где 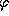-- угол поворота Земли. Интегрируя, получаем:

Если бы Земля вращалась без ускорения, то мы имели бы, очевидно,

так что дополнительный угол есть

Осталось вычислить угловое ускорение Земли. За 1 сутки продолжительность суток возрастает на

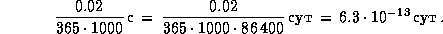
Поэтому угловая скорость, первоначально равная

через сутки станет

Приращение угловой скорости за 1 сутки есть

а угловое ускорение

Отсюда

В этой задаче поразителен не только ответ. Еще более удивительно, что столь малое угловое ускорение ( ) все же удалось обнаружить и измерить. Сделано это было путем анализа древних хроник (!), содержащих описания солнечных затмений (поймите, в чем здесь дело, самостоятельно).

Инструменты

3.1 При обнаружении камерой препятствия на пути марсохода передатчик сообщит об этом на Землю, и Центр управления в ответ пошлет сигнал двигателю аппарата. Сигнал должен прийти до того, как марсоход достигнет препятствия. Поскольку 1 а.е. -- это 500 световых секунд, на преодоление расстояния в 3 а.е. (удвоенное среднее расстояние от Земли до Марса) уходит 1500 с. Поэтому безопасная скорость движения марсохода не более 10 / 1500 м/с = 7 мм/с, или около 40 см/мин. Поистине черепашья скорость! Вспомните теперь, в каких пределах меняется геоцентрическое расстояние Марса и уточните найденную оценку. Быстрее всего марсоход мог бы двигаться при великих противостояниях Марса, когда r уменьшается до 55 миллионов км. Они всегда бывают в одно и то же время года (в августе -- сентябре). Как вы думаете, почему?

После того, как рукопись с приведенным только что текстом решения была сдана в издательство, произошли замечательные события, непосредственно относящиеся к теме этой задачи. 4 июля 1997 г. космический аппарат "Pathfinder" ("Следопыт") совершил посадку на поверхность Марса. Вскоре небольшой управляемый с Земли шестиколесный марсоход размером с большую детскую игрушку (его длина -- 65 см) пополз по Марсу со скоростью

см/с -- в полном согласии с полученной только что оценкой.

Метеостанция, установленная на "Следопыте", ведет измерения температуры марсианского "воздуха" в месте посадки. Днем она поднимается до C, ночью падает до C. Любопытно, что самая низкая температура воздуха, зафиксированная на Земле, практически такая же ( C, станция "Восток", Антарктида, 21 июля 1983 г.).

Чтобы обеспечить всем быстрый и надежный доступ к информации о Pathfinder'е, текущей и архивной, НАСА размещает ее в Интернете одновременно на многих серверах ("зеркалах"), разбросанных по всему земному шару. Если вам окажется трудно "пробиться" непосредственно в НАСА по одному из следующих адресов:

http://mpfwww.jpl.nasa.gov

или

http://mpfwww.arc.nasa.gov

можете попробовать воспользоваться сервером Института Космических Исследований (ИКИ) в Москве:

http:/www.iki.rssi.ru/jplmirror/mars

или, скажем, следующим датским:

http://sunsite.auc.dk/mars.

В первые дни после посадки "Следопыта" на Марс за информацией о нем по Интернету ежедневно поступало до 100 миллионов обращений! Система "зеркал" даже в самые горячие первые дни и часы позволяла получать текущую информацию о событиях на Марсе без сколько-нибудь серьезных задержек.

"Следопыт" -- первый из серии садящихся на Марс исследовательских аппаратов, запуск которых будет проведен НАСА в ближайшие годы. Предполагается, что в 2005 г. образцы марсианского грунта будут доставлены на Землю.

3.2 Любая экваториальная установка, в том числе и немецкая, будет одновременно и азимутальной, если телескоп установлен на полюсе -- неважно, южном или северном.

3.3 Всего глазом видно звезд, блеск их заключен между (Сириус) и 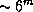. Глаз способен в принципе заметить разницу в , так что всего имеется градаций яркости. Это дает 7 бит информации на звезду. Кроме того, звезды различаются по цвету -- скажем, разных цветов (хотя вряд ли и это глаз способен различить у слабых звезд). Получаем еще три бита информации. Положение звезды на небе в дотелескопическую эпоху можно было определить с точностью в лучшем случае 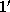в . В радиан содержится угл. минут. Координат две, но вторая (скажем, 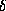) изменяется всего в пределах , а потому ее задание с точностью до 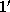предоставляет (а не ) возможностей. Всего -- 27 бит для положения звезды.

Итак, о каждой звезде можно было получить следующее количество информации: 7 битов -- блеск, 3 бита -- цвет, 27 битов -- положение; итого 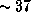битов на звезду. Общее количество информации о звездах, доступной людям в дотелескопическую (а правильнее будет, пожалуй, даже сказать -- и во всю доспектроскопическую) эпоху развития астрономии, буквально поражает своей мизерностью: 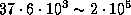бит килобайт.

Конечно, любой, даже самой простой дискетки на 360 килобайт, о каких все успели уже давно забыть, хватило бы за глаза для записи всех этих данных. Реально же к моменту изобретения телескопа было собрано менее 10% этой информации -- каталогов слабых по меркам того времени звезд 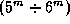не существовало, блеск и цвет оценивались грубо.

А как обстоит дело сегодня? Вот данные о количестве информации, собранной астрометрической космической обсерваторией HIPPARCOS. Она работала с конца 1989 г. по июнь 1993 г. и передала за это время на Землю Гигабайт 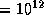байт данных. Результат обработки этих данных -- каталог HIPPARCOS'а (июнь 1997 г.). Для звезд их положения на небе даны в нем с миллисекундной точностью, еще для звезд -- с точностью миллисекунд. HIPPARCOS получил также ценнейшие данные о собственных движениях и о параллаксах звезд. В частности, им впервые надежно измерены тригонометрические параллаксы цефеид, а это -- основа построения шкалы расстояний во Вселенной.

3.4 Расстояние от Земли до Луны равно примерно 400000 км, а разрешение глаза 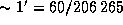радиана. Поэтому наименьший линейный размер образований на Луне, различимых невооруженным глазом, составляет 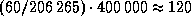км. Наибольшие кратеры имеют чуть больший размер и близки к пределу разрешения. В бинокль с шестикратным увеличением кратеры уже хорошо видны.

3.5 Размер наименьших деталей на Земле l, которые можно сфотографировать из космоса, определяется угловым размером диска дрожания звезды. Примем его значение равным одной угловой секунде. Тогда при расстоянии в 200 км от поверхности Земли имеем м. Пользуясь ухищрениями, добиваются и большего разрешения, но как -- это уже, вероятно, военный секрет Полишинеля. Не будем его раскрывать.

А чем определяется наименьший размер деталей на Луне, которые можно сфотографировать из космоса?

3.6 Оценим радиус R тела, которое на гелиоцентрическом расстоянии r = 40 а.е. (середина пояса Койпера) имеет звездную величину (проницающая сила наземных 10-метровых телескопов Кека и космического телескопа Хаббла). Освещенность от тела на Земле (или на Солнце, расстояние от Земли до Солнца много меньше расстояния до тела) равна

где -- "светимость" обращенного к нам полушария тела, A -- альбедо тела, -- освещенность от Солнца на поверхности тела. (Как вы думаете, почему в данном случае вместо казалось бы очевидного точного равенства ?) Освещенности от Солнца на Земле и на теле пояса Койпера относятся как

Поэтому

Обратите внимание, что освещенность убывает здесь как четвертая степень, а не как квадрат расстояния! С другой стороны,

где -- видимая звездная величина Солнца ( ), m -- видимая звездная величина тела ( -- предел, доступный телескопу Хаббла). Из двух последних выражений получаем

Принимая альбедо равным 0.2 и подставляя r = 40 а.е., находим км. Обратите внимание, что , так что на ближнем и на дальнем краях пояса Койпера значения R различаются в 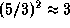раза.