Постановка задачи нахождения корней уравнения. Понятие точности приближенного значения корня уравнения. Этапы нахождения приближенных значений корней уравнения.

Задача решения уравнения заключается в нахождении множества всех корней этого уравнения.

Все методы решения нелинейных уравнений подразделяются на прямые и итерационные (приближенные). Прямые методы позволяют найти решение непосредственно с помощью формул и обеспечивают получение точного решения, например, квадратного или биквадратного уравнений. Однако во многих практических задачах алгебраическое или трансцендентное уравнение имеет достаточно сложный вид, и применить для его решения прямой метод не удается. Кроме того, в ряде случаев коэффициенты уравнения заданы приближенно (найдены опытным путем) и, следовательно, сама задача о точном определении корней уравнения не имеет смысла. В этих случаях применяют итерационные методы, позволяющие находить корни уравнения с наперед заданной степенью точности.

Поясним, что вычислить корень с заданной степенью точности, например, ε означает найти такое приближенное значение 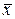которое отличается от точного значения ξ искомого корня на величину, не превышающую ε, т. е 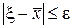. Пусть известно, что искомый корень ξ заключен между числами a и b, т. е. a ≤ ξ ≤ b, причем b - a ≤ ε. Тогда и a и b могут быть приняты за приближенные значения корня ξ соответственно с недостатком и с избытком с точностью до ε, так как 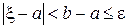и 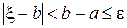. В общем случае, за приближенное значение корня ξ с точностью до ε можно принять любое число, содержащееся между a и b. Например, если корень ξ заключен между 4,35 и 4,37 (4,35 ≤ ξ ≤ 4,37), то за приближенное значение корня с точностью до ε = 0,02 можно принять число 4,35 или число 4,37, или любое число, заключенное между ними.

В этой и следующей теме 3 рассматриваются способы приближенного решения уравнения. Задача нахождения приближенного значения корня уравнения распадается на два этапа:

1) отделение корней;

2) уточнение корня до заданной степени точности.

Алгебраические уравнения, их свойства. Кратность корня. Границы действительных корней алгебраических уравнений. Определение области существования корней трансцендентного уравнения

Границы действительных корней алгебраических уравнений

Для алгебраического уравнения вида

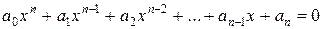, (4)

с действительными коэффициентами a₀, a₁, a₂, …, a_n (a₀ >0) область существования корней может быть установлена с помощью формулы Лагранжа

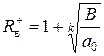, (5)

где 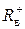- верхняя граница положительных корней уравнения (4);

k ≥ 1 - номер первого из отрицательных коэффициентов полинома

;

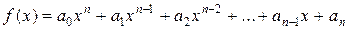B - наибольшее из абсолютных значений отрицательных коэффициентов полинома f(x).

Все положительные корни x⁺ уравнения (4) удовлетворяют неравенству .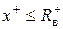

Нижнюю границу 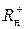положительных корней, верхнюю 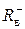и нижнюю границы 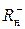отрицательных корней уравнения (4) определяют по формуле (5), применяя её для нахождения верхних границ положительных корней вспомогательных уравнений:

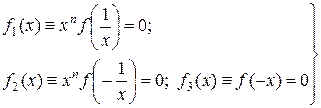(6)

Эти вспомогательные уравнения получают из исходного уравнения (4) заменой переменной x на 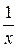, , 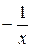– x.

Если R₁, R₂, R₃ - верхние границы положительных корней соответствующих вспомогательных уравнений, то для исходного уравнения (4) имеем:

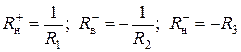и, следовательно все отличные от нуля действительные корни уравнения (если они существуют) лежат внутри интервалов

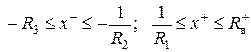Пример 1. По формуле Лагранжа определить границы области существования положительных и отрицательных корней уравнения

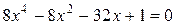Решение. В исходном уравнении: a_{0 =} 8, a₁ = 0, a₂= -8, a₃ = -32, a₄ = 1. Номер первого из отрицательных коэффициентов k = 2. Наибольший по абсолютному значению из отрицательных коэффициентов полинома f(x)) B = 32.

По формуле Лагранжа получаем

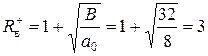Построим вспомогательное уравнение

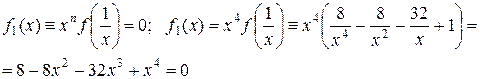
или

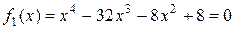Для него имеем: a_{0 =} 1, a₁ = -32, a₂= -8, a₃ = 0, a₄ = 8, k = 1 и B = 32. Следовательно, для вспомогательного уравнения 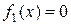верхней границей его положительных корней является R₁ = 1+32 = 33.

Строим вспомогательное уравнение .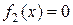

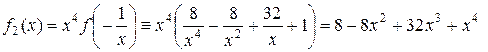или

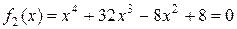Для этого уравнения имеем: a_{0 =} 1, a₁ = 32, a₂= -8, a₃ = 0, a₄ = 8, k = 2 и B = 8. Следовательно, для вспомогательного уравнения 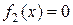верхней границей его положительных корней будет

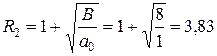Строим вспомогательное уравнение .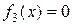

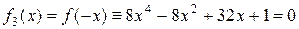Для него имеем: a_{0 =} 8, a₁ = 0, a₂= -8, a₃ = 32, a₄ = 1, k = 2 и B = 8. Следовательно, для вспомогательного уравнения 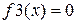верхней границей его положительных корней будет

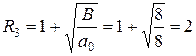Таким образом, если исходное уравнение 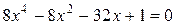имеет действительные корни, то они обязательно лежат в интервалах

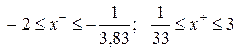Для определения области существования корней трансцендентного уравнения вида 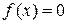рекомендуется следующая последовательность действий:

1. Преобразовать исходное уравнение вида к равносильному ему уравнению вида 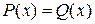, выбрав, если это возможно, функции P(x) и Q(x) такими, чтобы области их значений были разными.

2. Найти общую область определения X_PQ и общую область значений Y_PQ функций P(x) и Q(x).

3. Найти область корней R исходного уравнения, считая, что это есть область X_PQ или её подобласть, в которой значения функций P(x) и Q(x) не выходят за пределы области Y_PQ.

Пример 2. Определить область существования корней уравнения

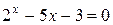Решение. Заменим данное уравнение равносильным уравнением вида 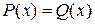. Например, 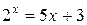. Найдем области определения и области значений полученных функций P(x) и Q(x):

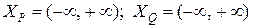т. е. X_P = X_Q и, следовательно, 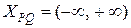. На этом интервале

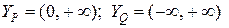Так как 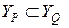, то .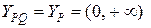

Найдем область корней уравнения. Ограничивая область значений функции 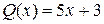областью 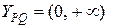, получим неравенство 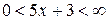. Его решение дает область 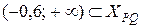. Поэтому корни уравнения 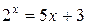и, следовательно, исходного уравнения 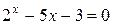, если они есть, заключены в интервале .

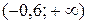Графический и аналитический методы отделения корней. Способы графического метода отделения корней. Теоремы, составляющие основу аналитического метода отделения корней. Алгоритм отделения корней аналитическим методом.

Отделить корни - это значит установить в области существования всех корней уравнения отрезки, в каждом из которых содержится один и только один корень уравнения. Отделение корней - поисковый этап решения уравнения. На начальной стадии этого этапа аналитическими методами определяется область существования корней уравнения. Затем в этой области графически или аналитически производится выделение отрезков, содержащих по одному корню.

Дата добавления: 2019-01-14; просмотров: 703; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 5 678 Следующая ⇒

Мы поможем в написании ваших работ!