Тема 1. Элементы теории погрешностей

(Лк –0,25 ч., ПЗ – 2 ч., СРС – 8 ч.).

Вопросы

1. Точные и приближенные числа. Абсолютная и относительная погрешности. Основные источники и классификация погрешностей.

2. Десятичная запись приближенных чисел. Значащая цифра. Верные значащие цифры. Округление чисел. Связь между числом верных знаков и погрешностью числа.

3. Погрешности суммы и разности. Потеря точности при вычитании близких чисел.

4. Погрешности произведения. Число верных знаков произведения.

5. Погрешности произведения и частного. Число верных знаков частного.

6. Относительная погрешность степени и корня.

7. Погрешности вычисления значений функции.

Литература

1. Демидович Б.П. Основы вычислительной математики: учебное пособие / Б.П. Демидович, И.А. Марон.- СПб: Лань, 2007. С. 17-42.

2. Данилина Н.И. Вычислительная математика: учебное пособие / Н.И. Данилина и др. М.: Высш. шк., 1985. С. 8-31.

3. Копченова Н.В. Вычислительная математика в примерах и задачах: учебное пособие /Н.В. Копченова, И.А. Марон.- СПб: Лань, 2008. С. 9-21.

Точные и приближенные числа. Абсолютная и относительная погрешности. Основные источники и классификация погрешностей.

При решении задач имеют дело с различными числами, которые могут быть точными или приближенными. Точные числа дают истинное значение величины числа, приближенные – близкое к истинному значению, причем степень близости определяется погрешностью способа нахождения этого числа: вычислением, измерением или иным способом.

Например, в утверждениях «На рабочем участке цеха установлено 7 станков», «на лекции присутствует 18 студентов», «в контейнере находится 214 заготовок» числа 7, 18, 214 – точные.

В утверждениях «масса станка 1570 кг», «ширина прохода между станками 2 м», «диаметр валика 20,48 мм» - приближенные. В последних утверждениях приближенные значения чисел обусловлены, прежде всего, несовершенством измерительных приборов, инструментов, которые были использованы при нахождении значений измеряемых величин. В последнем утверждении, кроме того, приближенность числа заключена в самом понятии диаметра заготовки. Строго говоря, поперечное сечение цилиндрической заготовки не является кругом, и говорить о ее диаметре можно лишь приближенно.

В отдельных случаях одно и то же число может быть и точным и приближенным. Например, число 3 является точным числом, если речь идет о количестве операций обработки поверхности заготовки, и оно же является приближенным, если его использовать как значение массы обрабатываемой заготовки.

Определение 1. Приближенным числом a называется число, незначительно отличающееся от точного числа A и заменяющего его в вычислениях.

Под ошибкой или погрешностью Δa приближенного числа a понимается разность между соответствующим точным числом A и данным приближением, т. е.

Если A > a, то ошибка положительна: ; если же A < a, то ошибка отрицательна: . Обычно знак ошибки неизвестен, поэтому обычно используется абсолютная погрешность приближенного числа

Определение 2. Абсолютной погрешностью Δ приближенного числа a называется абсолютная величина разности между соответствующим точным числом A и числом a, т. е.

Как правило, точное число A неизвестно, поэтому вместо неизвестной теоретической погрешности Δ используется верхняя граница ее абсолютной величины (предельная абсолютная погрешность).

Определение 3. Абсолютной погрешностью приближенного числа a называется величина Δ_a, удовлетворяющая неравенству

. (1)

Отсюда следует, что точное число A заключено в границах

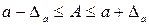Последнее неравенство обычно записывают в краткой форме

Сформулированное в определении 3 понятие абсолютной погрешности является весьма широким, так как в качестве Δ_a может быть взято любое положительное число, удовлетворяющее неравенству (1). На практике стремятся брать по возможности наименьшее число, удовлетворяющее неравенству (1).

Пример. Определить абсолютную погрешность числа a = 3,14, заменяющее число π.

Решение. Так как имеет место неравенство

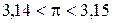, то

и, следовательно, можно принять Δ_a = 0,01.

Если учесть, , то будем иметь лучшую оценку: Δ_a = 0,002.

Абсолютная погрешность не достаточна для оценки точности измерения или вычисления. Действительно, если при измерении длины и диаметра стержня получены результаты l = 90,6 см ± 0,1 см и d = 8,3 см ± 0,1 см, то несмотря на совпадение абсолютных погрешностей, качество измерения длины стержня выше, чем его диаметра. Поэтому для оценки качества измерения или вычисления введено понятие относительной погрешности.

Определение 4. Относительной погрешностью приближенного числа a называется величина δ, равная отношению абсолютной погрешности Δ этого числа к модулю соответствующего точного числа A (A ≠ 0)

Так как на практике A ≈ a, то обычно используют формулу . Учитывая, что можем получить

Пример. Точное число A находится на отрезке [23,07; 23,10]. Определить его приближенное значение, абсолютную и относительную погрешности.

Решение. За приближенное значение примем середину заданного отрезка: a = 23, 085. Абсолютная погрешность есть половина его длины:

Δ_a = 0,015. Относительную погрешность находим по формуле

Величину погрешности принято округлять до одной-двух отличных от нуля цифр. Поэтому можем положить δ_a = 0,07%.

Отметим, что в подобного рода задачах округление погрешности выполняется в сторону ее увеличения, чтобы обеспечить выполнение неравенства (1).

Основные источники и классификация погрешностей. Погрешности, возникающие при решении технических задач, могут быть разбиты на пять групп.

1. Погрешности, связанные с построением математической модели исследуемого объекта (процесса, явления и т. п.). Для реальных объектов весьма редко удается построить их точные математические модели, а вводимые различные упрощения позволяют получить лишь более или менее идеализированные модели, что вызывает ряд погрешностей, называемых погрешностями задачи.

Кроме того, нередко возникает ситуация, когда решить задачу в ее точной постановке трудно и даже невозможно. В этих случаях исходную задачу заменяют близкой по результатам приближенной задачей. При этом возникает так называемая погрешность метода.

2. Во многих решаемых задачах в качестве исходных данных выступают величины, значения которых получены экспериментально, а также различные физические константы, которые сами по себе являются приближенными числами. Использование таких величин вызывают погрешности, которые принято называть погрешностями исходной информации.

3. Погрешности, обусловленные необходимостью выполнения бесконечного вычислительного процесса. Например, различные математические функции задаются в виде бесконечных последовательностей или рядов, в частности

Так как бесконечный процесс не может быть завершен за конечное число шагов, то его прерывают на некотором члене последовательности, считая его приближением к искомому решению. В результате возникает погрешность, называемую остаточной погрешностью.

4. Погрешности, вызванные округлением чисел. Например, полагая , получаем Δ = 0,0004. Иногда приходится округлять и конечные числа, имеющие большое количество знаков. В результате возникает погрешность округления.

5. Погрешности, связанные с выполнением действий над приближенными числами, погрешности которых в определенной степени переносятся в результат вычислений (вычислительная погрешность или погрешность действий).

Дата добавления: 2019-01-14; просмотров: 1512; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 7 8 Следующая ⇒

Мы поможем в написании ваших работ!