Относительная погрешность степени и корня
Пусть имеем приближенное число a1 имеющее относительную погрешность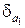 
. Оценим относительную погрешность степени 
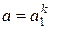. Очевидно,
.
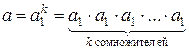Относительная погрешность произведения составляет
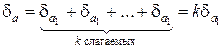. (17)
Таким образом, при возведении в степень k приближенного числа a1 его относительная погрешность увеличивается в k раз. В расчетах при возведении в степень приближенного числа в результате оставляют столько значащих цифр, сколько их имело само приближенное число.
Пусть имеем приближенное число a1 имеющее относительную погрешность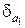 
. Доказано, что относительная погрешность корня 
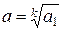в k раз меньше относительной погрешности числа a1
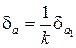. (18)
В расчетах при извлечении корня из приближенного числа в результате оставляют столько значащих цифр, сколько их имело подкоренное число.
Погрешности вычисления значений функции.
Основная задача теории погрешности заключается в следующем: известны погрешности некоторой системы величин и требуется определить погрешность заданной функции от этих величин.
Пусть задана дифференцируемая функция
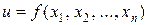
и пусть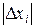 
(i = 1, 2, …, n) – абсолютные погрешности аргументов функции. Тогда абсолютная погрешность функции
.
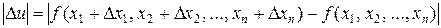Поскольку обычно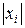 
- малые величины, то их произведениями, квадратами и высшими степенями можно пренебречь. Поэтому можно положить
|
|
|
.
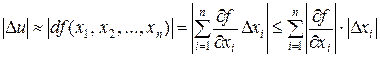Итак,
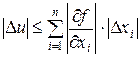. (19)
Обозначая через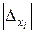 
(i = 1, 2, …, n) – абсолютные погрешности аргументов функции xi и через Δu – погрешность функции, получим
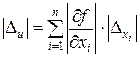. (20)
Разделив обе части уравнения (20) на u, находим относительную погрешность функции u
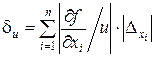. (21)
Формулы (20, 21) определения погрешности функции широко используются при оценке погрешностей измерения величин косвенным методом.
Контрольные вопросы и упражнения для приобретения
Умений и навыков по теме 1
1. Приведите утверждения (не менее 5-6), в которых используются точные числа и утверждения с приближенными числами.
2. Назовите две-три причины, обусловливающие приближенные значения чисел. В каких случаях одно и то же число может быть точным и приближенным?
3. Что понимается под погрешностью приближенного числа? Дайте определение понятия «абсолютная погрешность приближенного числа».
4. Как записывается интервал, в котором заключено точное число A? Найдите абсолютную погрешность числа a = 3,14, заменяющее число π.
5. Дайте определение понятия «относительная погрешность приближенного числа». Приведите подробное решение следующей задачи.
|
|
|
Задача. Точное число A находится на отрезке [48,24; 48,27]. Определить его приближенное значение, абсолютную и относительную погрешности.
6. Отобразите в графической форме классификацию погрешностей. Приведите один-два примера источника возникновения каждой из указанных в классификации погрешностей.
7. Запишите в виде многочлена m степени числа 8510,480; 0,004308 и 567000. Отметьте подчеркиванием те нули в этих числах, которые не считаются значащими.
8. Какие значащие цифры в ниже приведенных приближенных числах считаются верными? Сколько верных знаков имеются в числе x, если известна его абсолютная погрешность Δx:
а) x = 0,3941, Δx = 0,25·10-2; б) x = 0,2461, Δx = 0,1·10-3; в) x = 279,394, Δx = 0,1.
9. Какими формулами описывается связь между относительной погрешностью приближенного числа и количеством его верных знаков в узком и широком смысле? Определить количество верных цифр в числе x, если известна его относительная погрешность δx:
а) x = 1,3941, δx = 0,1·10-2; б) x = 0,2561, δx = 0,2·10-1; в) x = 79,384, δx = 0,1.
10. Чему равна абсолютная погрешность суммы приближенных чисел? Как поступают при сложении чисел различной абсолютной точности?
11. Из каких слагаемых складывается погрешность суммы приближенных чисел. Пояснить на примере.
|
|
|
12. Найти суммы приближенных чисел и их абсолютные и относительные погрешности:
а) 0,145+321+78,2 (все знаки верные); б) 0,301+193,1+11,58 (все знаки верные); в) x1 + x2 – x3, где x1 = 197,6;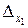 
= 0,2; x2 = 23,44; 
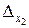= 0,22; x3 = 201,55; 
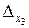= 0,17.
13. Чему равны абсолютная и относительная погрешность разности приближенных чисел? В каком случае возникает при вычитании приближенных чисел потеря точности? Поясните примером.
14. Чему равны абсолютная и относительная погрешности произведения приближенных чисел? Как изменяются абсолютная и относительная погрешности приближенного числа при умножении его на точный сомножитель k?
15. Сколько верных цифр может иметь произведение, если число сомножителей не более 10?
16. Длина и ширина токарно-винторезного станка 1К62 составляют 2,505±0,001 м и 1,190±0,001 м соответственно. Вычислить занимаемую станком площадь, указать абсолютную и относительную погрешности результата.
17. Чему равны абсолютная и относительная погрешности частного при делении приближенных чисел? Как определяется число верных знаковчастного?
18. Найти частное приближенных чисел и их абсолютные и относительные погрешности, считая все знаки в исходных данных верными:
|
|
|
а) 5,684:5,032; б) 0,144:1,2; в) 216:4.
19. Измерена глубина h вдавливания в стальную пластину шарика диаметром D=10 ±0,01 мм силой P = 9810 ±0,1 Н. Величина h составила h = 0,38±0.02. Определить по формуле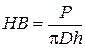 
твердость по Бринеллю, абсолютную и относительную погрешности результата вычисления твердости.
Тема 2. Методы решения нелинейных уравнений
Лк –1,5 ч., ПЗ – 2 ч., СРС – 8 ч.).
Вопросы
1. Алгебраические и трансцендентные уравнения. Понятия алгебраической функции, алгебраической рациональной, дробно-рациональной и иррациональной. Трансцендентные функции.
2. Постановка задачи нахождения корней уравнения. Понятие точности приближенного значения корня уравнения. Этапы нахождения приближенных значений корней уравнения.
3. Алгебраические уравнения, их свойства. Кратность корня. Границы действительных корней алгебраических уравнений. Определение области существования корней трансцендентного уравнения вида 
.
4. Графический и аналитический методы отделения корней. Способы графического метода отделения корней. Теорема, составляющая основу аналитического метода отделения корней. Алгоритм отделения корней аналитическим методом.
Литература
1. Демидович Б.П. Основы вычислительной математики: учебное пособие / Б.П. Демидович, И.А. Марон.- СПб: Лань, 2007. С. 112-117, 158-165.
2. Данилина Н.И. Вычислительная математика: учебное пособие / Н.И. Данилина и др. М.: Высш. шк., 1985. С. 162-174, 201-207.
Дата добавления: 2019-01-14; просмотров: 2145; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!