Погрешности произведения. Число верных знаков произведения
Пусть имеем два точных числа A1 и A2 и их приближенные значения a1 и a2. Найдены произведения A = A1A2 и a = a1a2.
В работе [1] достаточно просто доказано, что относительная погрешность 
произведения a = a1a2 не превышает сумму относительных погрешностей 
и 
приближенных чисел a1 и a2
.
В практических расчетах полагают, что
. (11)
Последнее распространяется на произведение нескольких приближенных чисел a = a1a2…an
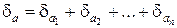. (12)
Зная относительную погрешность 
произведения a можно определить его абсолютную погрешность по формуле 
.
Замечание. При умножении приближенного числа a на точный сомножитель k относительная погрешность произведения равна относительной погрешности приближенного числа a, а абсолютная погрешность в |k | раз больше абсолютной погрешности приближенного числа
. (13)
Согласно (12), относительная погрешность произведения не может быть меньше, чем относительная погрешность наименее точного из сомножителей. Поэтому здесь, как и в случае сложения, не имеет смысла сохранять в более точных сомножителях излишнее количество значащих цифр.
Отсюда при умножении чисел различной абсолютной точности поступают следующим образом:
1) выделяют число (или числа), имеющее наибольшую абсолютную погрешность; остальные числа округляют по образцу выделенных, сохраняя один запасной десятичный знак;
|
|
|
2) производят умножение чисел, учитывая все сохраненных знаки; в полученном результате сохраняют столько значащих цифр, сколько их имеется в наименее точном из сомножителей.
Пример. Найти произведение приближенных чисел a1 = 2,5 и a2 = 72,397, имеющие верные все написанные цифры.
Решение. Применяя выше приведенные действия, получим
a = a1a2 = 2,5·72,4 = 181 ≈ 1,8·102.
Число верных знаков произведения. Пусть имеем произведение n сомножителей (n ≤ 10) a = a1a2…an, где ai ≠ 0, каждый из которых имеет, по крайней мере, m (m > 1) верных цифр.
Любой сомножитель ai может быть представлен в виде
,
где α1, α2, …, αn – первые значащие цифры множителей.
Тогда по формуле (5) будем иметь 
и, следовательно,
. (14)
Так как 
, то 
.
Таким образом, если все сомножители имеют m верных цифр и число сомножителей не более 10, то число верных цифр произведения на одну или две единицы меньше m. В случае, когда сомножители имеют различную точность, под m следует понимать число верных цифр наименее точного из сомножителей.
Пример. Определить относительную погрешность и количество верных цифр произведения a = 17,63·14,285.
|
|
|
Решение. Так как m = 4, то по формуле (14) имеем
.
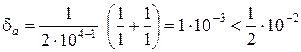Следовательно, произведение имеет две верные цифры.
5. Погрешности частного. Число верных знаков частного [2]
Пусть имеем два точных числа A1 и A2 и их приближенные значения a1 и a2 с абсолютными погрешностями 
, . Поставлена задача: оценить относительную погрешность приближенного значения частного a = a1/a2 для точного значения A = A1/A2.
Если a = a1/a2, то 
и 
. Отсюда
,
т. е. относительная погрешность частного не превышает суммы относительных погрешностей делимого и делителя.
Следствие. Если a = a1/a2, то
. (15)
Согласно (15), относительная погрешность частного не может быть меньше, чем относительная погрешность наименее точного из чисел a1 и a2. Поэтому здесь, как и в случае умножения, не имеет смысла сохранять в более точном числе a1 или a2 излишнее количество значащих цифр и в случае деления чисел различной абсолютной точности поступают следующим образом:
1) выделяют число, имеющее наибольшую абсолютную погрешность, т. е. наименьшее количество верных цифр; второе число округляют по образцу выделенного, сохраняя один запасной десятичный знак;
2) производят деление чисел, учитывая все сохраненных знаки; в полученном результате сохраняют столько значащих цифр, сколько их имеется в наименее точном из сомножителей.
|
|
|
Число верных знаков частного. Поступая также, как при определении верных знаков произведения [1, 2], получим
. (16)
Отсюда следует правило: если α1 ≥ 2 и α2 ≥ 2, то частное a имеет, по меньшей мере, m -1 верных цифр; если α1 = 1 или α2 = 1, или α1 = α2 = 1, то частное a заведомо имеет m -2 верных цифр. В случае, когда числа a1 и a2 имеют различную точность, под m следует понимать число верных цифр наименее точного из них.
Пример. Вычислить частное a = 39,356:2, 21 и определить сколько в нем содержится верных цифр, если в делимом и делителе все цифры верные.
Решение. Поскольку в делителе три верные цифры, а в делимом – пять, то делимое округляем до четырех значащих цифр и производим деление. Получим a = 39,36:2, 21 = 17,81 ≈ 17,8 (в частном оставляем столько значащих цифр, сколько их содержится в числе с наименьшим количеством верных цифр).
Относительную погрешность найдем по формуле (16), где m =3, α1 = 3 и α2 = 2. Следовательно,
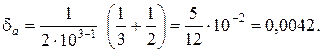
Таким образом, частное содержит две верные цифры. Если рассмотреть частное a = 39,356:1, 51, то получим a = 39,36:1, 51 = 26,06 ≈ 26,1 и согласно приведенному выше правилу получим
|
|
|
,
т. е. частное содержит только одну верную цифру. Действительно, вычислив абсолютную погрешность результата деления, находим
.
Окончательный результат следует записать в виде: a = 26±2. Заметим, что цифра 6 единиц частного является сомнительной ( 
=2 ≥ 0,5). Если записать результат только с верными значащими цифрами, то необходимо произвести округление и учесть погрешность округления, т. е.:
a1 = 3·101, 
.
Тогда a = (3±0,6)·101. Однако на самом деле абсолютная погрешность несколько меньше.
Дата добавления: 2019-01-14; просмотров: 1195; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!