Олимпиада «Океан знаний» 11 марта 2015 МАТЕМАТИКА
1. Докажите, что если 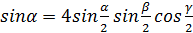 , то треугольник с углами
, то треугольник с углами 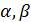 и
и 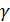 равнобедренный.
равнобедренный.
2. Найдите решение системы
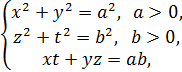
для которого величина 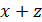 принимает наибольшее значение.
принимает наибольшее значение.
3. Все коэффициенты квадратного трёхчлена – нечётные целые числа. Докажите, что у него нет рациональных корней.
4. На сторонах остроугольного треугольника найдите три точки, являющиеся вершинами треугольника с минимальным периметром.
5. Точка Е – середина ребра 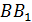 куба
куба 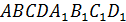 . Найдите тангенс угла между прямыми
. Найдите тангенс угла между прямыми 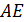 и
и 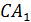 .
.
РЕШЕНИЯ
1. Докажите, что если 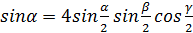 , то треугольник с углами
, то треугольник с углами 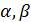 и
и 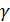 равнобедренный.
равнобедренный.
♦
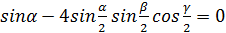 ,
,
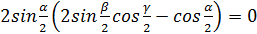 ,
,
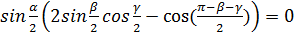 ,
,
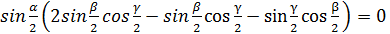 ,
,
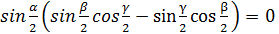 ,
,
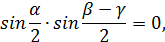
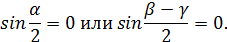
Для углов треугольника отсюда можно сделать только один вывод
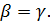
2. Найдите решение системы
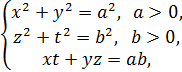
для которого величина 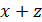 принимает наибольшее значение.
принимает наибольшее значение.
♦ Левая часть последнего уравнения напоминает скалярное произведение в координатной форме. Воспользуемся этим. Рассмотрим её как скалярное произведение векторов 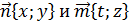 . Тогда
. Тогда

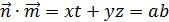 .
.
C другой стороны по определению скалярного произведения
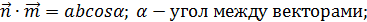
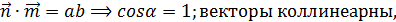 их координаты пропорциональны,
их координаты пропорциональны,
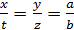 ;
; 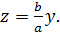
Тогда

Функция 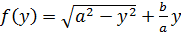 достигает максимума
достигает максимума 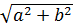 при
при 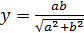 . Отсюда
. Отсюда
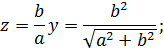
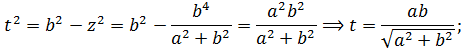
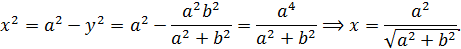
Таким образом, найдено решение, которое удовлетворяет условию задачи:
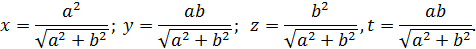
Докажем, что в любом решении системы числа 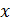 и
и 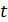 одного знака, а также, что числа
одного знака, а также, что числа 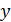 и
и 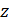 тоже одного знака. Оба произведения
тоже одного знака. Оба произведения 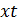 и
и 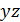 не могут быть одновременно отрицательными. Предположим, что одно из них положительно, а другое отрицательно; например,
не могут быть одновременно отрицательными. Предположим, что одно из них положительно, а другое отрицательно; например, 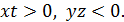 Так как
Так как 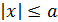 и
и 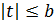 , то
, то 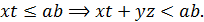 Противоречие. С учётом этого все остальные решения можно получить подбором знаков плюс или минус
Противоречие. С учётом этого все остальные решения можно получить подбором знаков плюс или минус
|
|
|
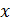
| 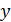
| 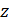
| 
| |
| 1 | + | + | + | + |
| 2 | + | – | – | + |
| 3 | – | + | + | – |
| 4 | – | – | – | – |
♦ Другое решение. Вид первого уравнения системы 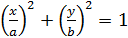 заставляет вспомнить теорему Пифагора и основное тригонометрическое тождество. Логична замена
заставляет вспомнить теорему Пифагора и основное тригонометрическое тождество. Логична замена 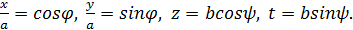 Из последнего уравнения системы имеем
Из последнего уравнения системы имеем 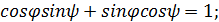
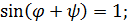
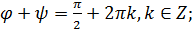
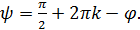
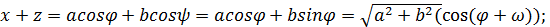
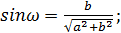
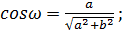
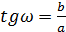 ;
;
преобразование провели с помощью метода введения дополнительного угла.
Наибольшее значение 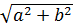 принимает при
принимает при 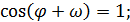
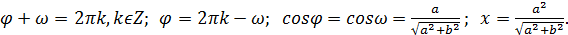
Ответ:
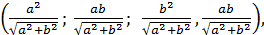
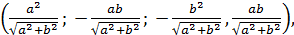
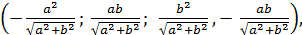
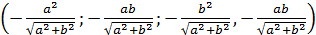
3. Все коэффициенты квадратного трёхчлена – нечётные целые числа. Докажите, что у него нет рациональных корней.
♦ Пусть 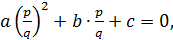 где
где 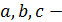 нечётные целые числа;
нечётные целые числа; 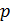 и
и 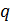 взаимно простые целые числа. Упростим равенство
взаимно простые целые числа. Упростим равенство 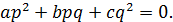 Если
Если 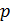 и
и 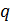 оба нечётные, то слева в равенстве нечётное число, а справа чётное. Противоречие. Если одно из них чётно, а другое нечётно, то в левой части одно слагаемое нечётно, а два чётные, их сумма – нечётное число, и оно не может равняться нулю.
оба нечётные, то слева в равенстве нечётное число, а справа чётное. Противоречие. Если одно из них чётно, а другое нечётно, то в левой части одно слагаемое нечётно, а два чётные, их сумма – нечётное число, и оно не может равняться нулю.
4. На сторонах остроугольного треугольника найдите три точки, являющиеся вершинами треугольника с минимальным периметром.
♦ Ответ: вершины треугольника с минимальным периметром – основания высот исходного треугольника.
|
|
|
Пусть 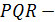 треугольник с минимальным периметром, вписанный в
треугольник с минимальным периметром, вписанный в 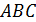 ;
; 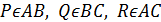 . Отразим точку Р симметрично относительно АС. Получим точку
. Отразим точку Р симметрично относительно АС. Получим точку 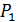 . Отразим точку Р симметрично относительно ВС. Получим точку
. Отразим точку Р симметрично относительно ВС. Получим точку 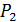 . Длина ломаной
. Длина ломаной 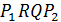 равна периметру треугольника
равна периметру треугольника 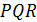 . Длина ломаной больше, чем длина отрезка, соединяющего её концы. В силу минимальности периметра длина ломаной
. Длина ломаной больше, чем длина отрезка, соединяющего её концы. В силу минимальности периметра длина ломаной 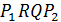 равна длине отрезка
равна длине отрезка 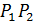 . Поэтому точки
. Поэтому точки 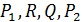 лежат на одной прямой. В треугольнике
лежат на одной прямой. В треугольнике 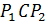 угол при вершине равен
угол при вершине равен 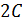 , боковые стороны равны
, боковые стороны равны 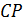 . В нём чем меньше боковая сторона, тем меньше основание
. В нём чем меньше боковая сторона, тем меньше основание 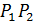 . Длина минимальной боковой стороны равна высоте треугольника АВС. Отсюда, СР – высота треугольника АВС. Аналогично доказывается, что
. Длина минимальной боковой стороны равна высоте треугольника АВС. Отсюда, СР – высота треугольника АВС. Аналогично доказывается, что 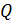 и
и 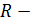 тоже основания высот.
тоже основания высот.
5. Точка Е – середина ребра 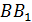 куба
куба 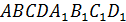 . Найдите тангенс угла между прямыми
. Найдите тангенс угла между прямыми 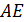 и
и 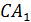 .
.
♦ Примем ребро куба за 1. Тогда 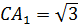 . Проведём прямую через точку
. Проведём прямую через точку 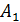 параллельно
параллельно 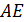 . Она пересекает продолжение ребра
. Она пересекает продолжение ребра 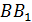 в точке
в точке 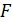 , причём
, причём 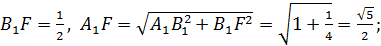
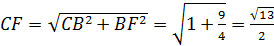 .
.
Искомый угол равен углу 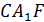 или смежному с ним. В треугольнике
или смежному с ним. В треугольнике 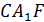
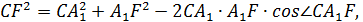
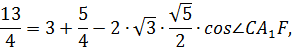
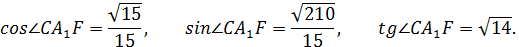
Ответ: 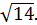
Олимпиада 2015 года по математике "Океан знаний"
ОТБОРОЧНЫЙ ДИСТАНЦИОННЫЙ ТУР
1. Угол 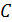 треугольника
треугольника 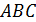 равен
равен 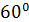 ,
, 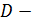 отличная от
отличная от 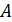 точка пересечения окружностей, построенных на сторонах
точка пересечения окружностей, построенных на сторонах 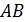 и
и 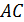 как на диаметрах. Известно, что
как на диаметрах. Известно, что 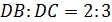 . Найдите угол
. Найдите угол 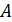 .
.
|
|
|
2. Решите уравнение 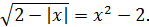
3. Решите уравнение в целых числах 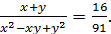
4. На счету Пети в банке 500 долларов. Петя может снять со счёта 300 долларов или положить на свой счёт 198 долларов. Какую максимальную сумму сможет снять Петя и за какое минимальное число операций, если у него нет других денег, кроме этих 500 на счёте?
5. Найдите все значения параметра 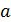 , для каждого из которых существует хотя бы одна пара чисел
, для каждого из которых существует хотя бы одна пара чисел 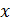 и
и 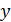 , удовлетворяющих неравенству
, удовлетворяющих неравенству
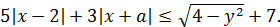
6. Решите систему
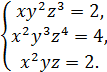
7. Найдите все функции 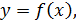 для которых в
для которых в 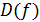 выполняется тождество
выполняется тождество
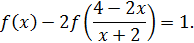
8. Докажите неравенство 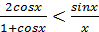 при
при 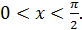
9. Все координаты вектора отличны от нуля, сумма координат равна 1, а сумма их обратных величин равна нулю. Чему равна длина вектора?
10. Каждый город одной страны связан авиамаршрутом ровно с тремя другими городами этой страны. Из каждого города можно перелететь в другой, сделав не более двух пересадок. Сколько городов в стране?
РЕШЕНИЯ
1. Угол 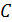 треугольника
треугольника 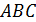 равен
равен 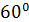 ,
, 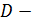 отличная от
отличная от 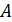 точка пересечения окружностей, построенных на сторонах
точка пересечения окружностей, построенных на сторонах 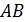 и
и 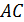 как на диаметрах. Известно, что
как на диаметрах. Известно, что 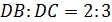 . Найдите угол
. Найдите угол 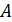 .
.
|
|
|
♦ Так как 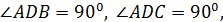 то точка
то точка 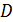 лежит на прямой
лежит на прямой 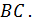 Возможны два случая:
Возможны два случая: 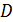 лежит на отрезке
лежит на отрезке 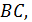 либо на продолжении отрезка
либо на продолжении отрезка 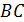 за точку
за точку 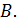 Точка
Точка 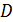 не может лежать на продолжении
не может лежать на продолжении 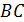 за точку
за точку 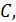 так как угол
так как угол 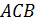 острый. Положим, что
острый. Положим, что 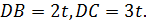 Так как
Так как 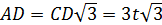 , то
, то 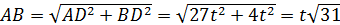 .
.
Рассмотрим первый случай. По теореме синусов
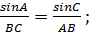
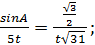
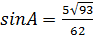 .
.
Во втором случае
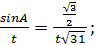
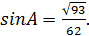
Ответ: 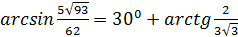 или
или 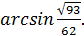
2. Решите уравнение 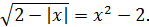
♦ Решение 1. После замены 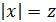 и возведения в квадрат обеих частей уравнения получим
и возведения в квадрат обеих частей уравнения получим
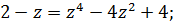
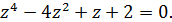
Корни 1 и –2 очевидны, поэтому уравнение можно записать так
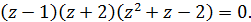
Осталось решить уравнение 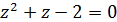 и сделать проверку.
и сделать проверку.
Ответ: 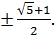
Решение 2. Замена 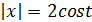 приводит уравнение к виду
приводит уравнение к виду
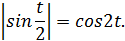
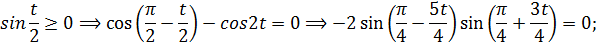
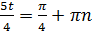 или
или 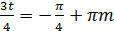
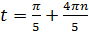 или
или 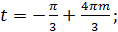
После отбора осталось 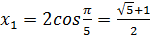
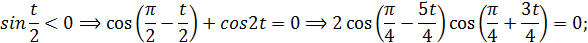
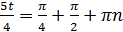 или
или 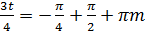
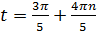 или
или 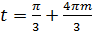 .
.
Ни одно значение не удовлетворяет взятым ограничениям.
Ответ: 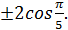
3. Решите в целых числах уравнение 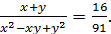
♦ Ответ: (5; 11), (11; 5).
Решение 1. Если пара чисел 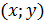 удовлетворяет уравнению, то пара
удовлетворяет уравнению, то пара 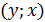 тоже удовлетворяет уравнению; оба числа не могут быть отрицательными одновременно. Поэтому достаточно найти решения, для которых
тоже удовлетворяет уравнению; оба числа не могут быть отрицательными одновременно. Поэтому достаточно найти решения, для которых 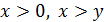 , и из них получить остальные.
, и из них получить остальные.
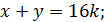
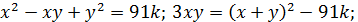
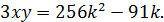
Все варианты значений 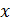 и
и 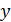 приводят к противоречию с тем, что
приводят к противоречию с тем, что 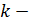 натуральное число. И лишь в одном случае противоречия нет:
натуральное число. И лишь в одном случае противоречия нет:
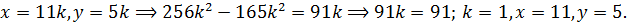
Решение 2.
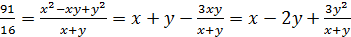 .
.
Пусть 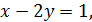 тогда
тогда 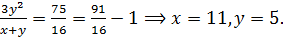 Другие предположения о значении
Другие предположения о значении 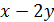 приводят к противоречию с условием задачи.
приводят к противоречию с условием задачи.
4. На счету Пети в банке 500 долларов. Петя может снять со счёта 300 долларов или положить на свой счёт 198 долларов. Какую максимальную сумму сможет снять Петя и за какое минимальное число операций, если у него нет других денег, кроме этих 500 на счёте?
Ответ. 498 долларов; 83 операции. Применим метод обратный ход. При каждой операции Петя снимает или кладёт на счёт сумму долларов, кратную шести. Конечный результат тоже должен делиться на 6, поэтому в итоге обналичить сумму в 500 и 499 долларов он не сможет. Число 498 делится на 6. Докажем, что такую сумму он снять сможет. Получить сумму 498 последней операцией он сможет, только если на счету было 302 доллара, а на руках у него было 198 долларов. Если бы он предпоследним ходом снимал 300, то на счету должно было бы быть 602, а это невозможно. Поэтому предпоследний ход мог быть только такой: положить 198 на счёт. Это значит, что перед предпоследним ходом на счету было 104, а на руках у Пети 396. Соответственно, перед этим ходом на счету было 404, а на руках у Пети 96. Найдём наименьшее число операций, которое даёт возможность Пете иметь на руках 96 долларов. Пусть для этого Петя х раз снимал и у вкладывал деньги на счёт, тогда
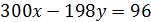
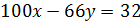
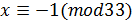
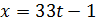
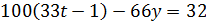 ,
, 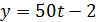 ,
, 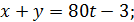
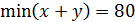 ,
, 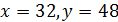 . Отсюда, 83 – минимальное количество операций, которое позволит Пете обналичить сумму в 498 долларов. Приведём схему получения 498 долларов за 83 операции.
. Отсюда, 83 – минимальное количество операций, которое позволит Пете обналичить сумму в 498 долларов. Приведём схему получения 498 долларов за 83 операции.
| На счету | 500 | 200 | 398 | 98 | 296 | 494 | 194 | 392 | 92 |
| В кармане | 0 | 300 | 102 | 402 | 204 | 6 | 306 | 108 | 408 |
| 290 | 488 | 188 | 386 | 86 | 284 | 482 | 182 | 380 | 80 |
| 210 | 12 | 312 | 114 | 414 | 216 | 18 | 318 | 120 | 420 |
| 278 | 476 | 176 | 374 | 74 | 226 | 470 | 170 | 368 | 68 |
| 222 | 24 | 324 | 126 | 426 | 228 | 30 | 330 | 132 | 432 |
| 266 | 464 | 164 | 362 | 62 | 260 | 458 | 158 | 356 | 56 |
| 234 | 36 | 336 | 138 | 438 | 240 | 42 | 342 | 144 | 444 |
| 254 | 452 | 152 | 350 | 50 | 248 | 446 | 146 | 344 | 44 |
| 246 | 48 | 348 | 150 | 450 | 252 | 54 | 354 | 156 | 456 |
| 242 | 440 | 140 | 338 | 38 | 236 | 434 | 134 | 332 | 32 |
| 258 | 60 | 360 | 162 | 462 | 264 | 66 | 366 | 168 | 468 |
| 230 | 428 | 128 | 326 | 26 | 224 | 422 | 122 | 320 | 20 |
| 270 | 72 | 372 | 174 | 474 | 276 | 78 | 378 | 180 | 480 |
| 218 | 416 | 116 | 314 | 14 | 212 | 410 | 110 | 308 | 8 |
| 282 | 84 | 384 | 186 | 486 | 288 | 90 | 390 | 192 | 492 |
| 206 | 404 | 104 | 302 | 2 | |||||
| 294 | 96 | 396 | 198 | 498 |
5. Найдите все значения параметра 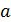 , для каждого из которых существует хотя бы одна пара чисел
, для каждого из которых существует хотя бы одна пара чисел 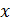 и
и 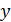 , удовлетворяющих неравенству
, удовлетворяющих неравенству
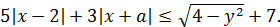
♦ Функция 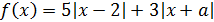 кусочно-линейная и при
кусочно-линейная и при 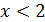 угловой коэффициент равен либо –2, либо –8, а при
угловой коэффициент равен либо –2, либо –8, а при 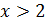 угловой коэффициент равен либо 2, либо 8. Значит, функция убывает при
угловой коэффициент равен либо 2, либо 8. Значит, функция убывает при 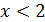 и возрастает при
и возрастает при 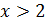 . Поэтому
. Поэтому 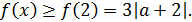
Для 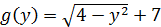 имеем
имеем 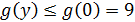 . Если
. Если 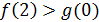 , то неравенство
, то неравенство 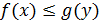 не имеет решений, так как
не имеет решений, так как 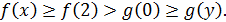 Если
Если 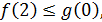 то пара чисел
то пара чисел 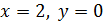 удовлетворяет неравенству
удовлетворяет неравенству 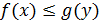 .
.
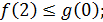
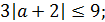
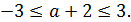
Ответ: 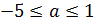 .
.
6. Решите систему
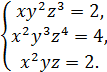
♦ Решение 1. Разделим второе уравнение на первое:
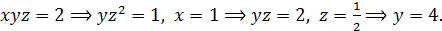 Ответ:
Ответ: 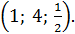
Решение 2. Из второго уравнения 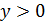 , тогда из третьего
, тогда из третьего 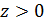 , а из первого
, а из первого 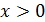 . Поэтому можно сделать замену
. Поэтому можно сделать замену 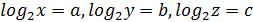 . Получим систему
. Получим систему
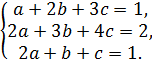
Вычтем из второго уравнение первое.
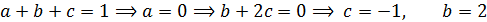
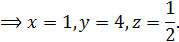
7. Найдите все функции 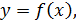 для которых в
для которых в 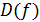 выполняется тождество
выполняется тождество
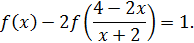
♦ Вместо 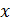 подставим в тождество
подставим в тождество 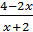 . Получим
. Получим
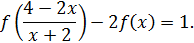
Возникла система
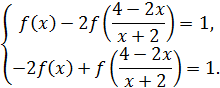
Прибавим к первому уравнению второе, умноженное на 2:
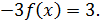
Ответ: 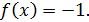
8. Докажите неравенство 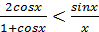 при
при 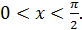
♦ Перепишем неравенство в виде 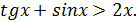 Функция
Функция 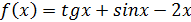 в заданной области возрастает, так как
в заданной области возрастает, так как 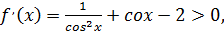 поэтому
поэтому 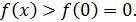
9. Все координаты вектора отличны от нуля, сумма координат равна 1, а сумма их обратных величин равна нулю. Чему равна длина вектора?
♦ Ответ: 1. 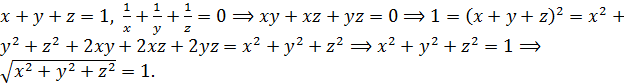
10. Каждый город одной страны связан авиамаршрутом ровно с тремя другими городами этой страны. Из каждого города можно перелететь в другой, сделав не более двух пересадок. Сколько городов в стране?
♦ Ответ: число городов чётно 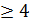 и не может быть более 22; примеры схем можно построить.
и не может быть более 22; примеры схем можно построить.
Дата добавления: 2018-11-24; просмотров: 196; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
