Владивосток, 21 ноября 2015 года
Класс
1. Существуют ли натуральные  для которых
для которых 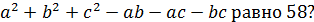
2. Найдите 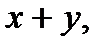 если
если 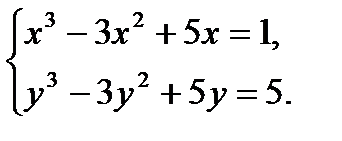
3. Окружности радиусов 13 и 35 с центрами  и
и  соответственно касаются внутренним образом в точке
соответственно касаются внутренним образом в точке 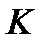 ;
; 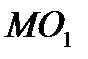 и
и 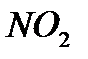 – параллельные радиусы этих окружностей, отложенные в одну полуплоскость относительно прямой
– параллельные радиусы этих окружностей, отложенные в одну полуплоскость относительно прямой 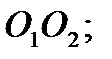
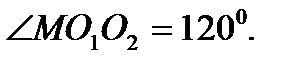 Докажите, что точки
Докажите, что точки 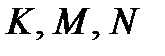 лежат на одной прямой.
лежат на одной прямой.
4. В квадрате со стороной 5 см размещено 126 точек. Докажите, что среди них существует 6 точек, которые лежат в круге радиуса 1 см.
5. Три смеси составлены из трёх элементов А, В и С. В первую смесь входят только А и В в весовом отношении 3:5. Во вторую смесь входят только элементы В и С в весовом отношении 1:2. В третью смесь входят только А и С в весовом отношении 2:3 В каком отношении нужно взять эти смеси, чтобы во вновь полученной смеси элементы А, В и С содержались в весовом отношении 3:5:2?
МУНИЦИПАЛЬНЫЙ ЭТАП
ВСЕРОССИЙСКОЙ ОЛИМПИАДЫ ПО МАТЕМАТИКЕ0
Владивосток, 14 ноября 2015 года
Класс
1. Какое наибольшее значение может принимать 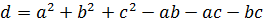 , если
, если  – двузначные натуральные числа и
– двузначные натуральные числа и 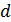 делится на 4?
делится на 4?
2. Найдите все значения a, при каждом из которых система имеет единственное решение
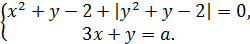
3. Множество М целых чисел (не всех) содержит вместе с любыми своими числами их разность, Докажите, что оно является множеством всех кратных некоторого  целого числа из этого же множества.
целого числа из этого же множества.
4. Про квадратный трёхчлен  известно, что
известно, что  при
при 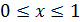 . Найдите наибольшее возможное значение
. Найдите наибольшее возможное значение 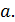
|
|
|
5. В окружность вписан правильный треугольник АВС, М – точка на дуге, соединяющей А и В. Докажите, что 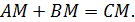
РЕШЕНИЯ ЗАДАЧ ГОРОДСКОЙ ОЛИМПИАДЫ 2015
8.1. Докажите, что 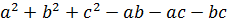 при нечётных натуральных
при нечётных натуральных  делится на 4.
делится на 4.
♦ 
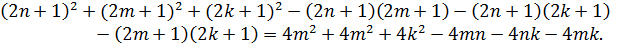
8.2. Представьте в виде произведения двух многочленов 
♦  =
= 
8.3. Одуванчик утром распускается, два дня цветёт жёлтым, на третий день утром становится белым, а к вечеру облетает. Вчера днём на поляне было 20 желтых и 14 белых одуванчиков, а сегодня 15 жёлтых и 11 белых. Сколько желтых одуванчиков было на поляне позавчера?
♦ Ответ: 25. Все одуванчики, которые позавчера были желтыми, стали белыми вчера или сегодня: 14 + 11 = 25.
8.4. В круге проведены два радиуса, не лежащие на одной прямой. Постройте хорду, делящуюся ими на три равные части.
♦ Пусть О – центр окружности ОА и ОВ – проведённые радиусы. Перпендикулярно биссектрисе угла АОВ проведём прямую 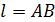 . Отложим во вне угла АОВ на прямой
. Отложим во вне угла АОВ на прямой 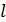 отрезки, равные отрезку, заключённому на этой же прямой между сторонами угла. Получим точки
отрезки, равные отрезку, заключённому на этой же прямой между сторонами угла. Получим точки 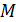 и
и 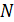 . Легко доказать, что прямые
. Легко доказать, что прямые 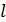 и
и 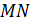 параллельны. По теореме Фалеса точки пересечения прямых
параллельны. По теореме Фалеса точки пересечения прямых  и
и  с окружностью и есть концы искомой хорды.
с окружностью и есть концы искомой хорды.
8.5. На доске записаны два числа 2014 и 2015. Петя и Вася ходят по очереди, начинает Петя. За один ход можно:
|
|
|
– либо уменьшить одно из этих двух чисел в его ненулевой цифре;
– либо разделить одно из чисел пополам, если оно чётное.
Выигрывает тот, кто первым напишет однозначное число. Кто из них может выиграть, как бы ни играл соперник? Опишите его стратегию и докажите, что она выигрышная.
♦ Ответ: Петя. Стратегия Пети: если можно одно из чисел заменить на однозначное, то сделать это; в противном случае уравнять два числа. Уравнять Петя всегда сможет, повторив ход Васи с тем числом, которое Вася не менял. Для доказательства устроим обратный ход. Допустим, Вася смог заменить число Х на однозначное. По стратегии Пети на доске перед этим было (Х; Х). Когда Петя делал предыдущих ход, то одно из чисел было Х. Поэтому Петя сам сделал бы его однозначным.
9.1. Существуют ли натуральные  для которых
для которых 
♦ Да. Пример 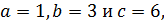
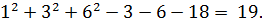
9.2. Найдите сумму корней уравнения 
♦ Ответ. +1.Корни –1 и 2.
9.3. Одуванчик утром распускается, два дня цветёт жёлтым, на третий день утром становится белым, а к вечеру облетает. Вчера днём на поляне было 20 желтых и 14 белых одуванчиков, а сегодня 15 жёлтых и 11 белых. Сколько белых одуванчиков будет на поляне завтра?
|
|
|
♦ Ответ: 9. Из вчерашних жёлтых одуванчиков 11 побелели сегодня, а остальные 20 – 11 = 9 побелеют завтра.
9.4. Решите систему

♦ Ответ: (–2; –2). Второе уравнение перепишем в виде

При исследовании первого уравнения возникают два случая.
1) 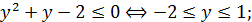
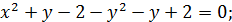
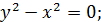
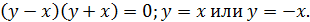
Если 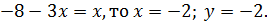 Решение (–2; –2) идёт в ответ.
Решение (–2; –2) идёт в ответ.
Если 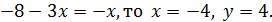 Пара (– 4, 4) не удовлетворяет условию
Пара (– 4, 4) не удовлетворяет условию  .
.
2) 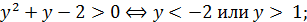

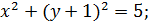
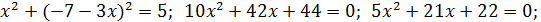
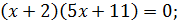
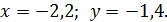
Пара (– 2,2; –1,4) не удовлетворяет условию 
9.5. На сторонах ромба 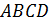 внешним образом построили равнобедренные треугольники
внешним образом построили равнобедренные треугольники 

 и
и  с углами
с углами 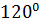 при вершинах
при вершинах  и
и  . Затем весь чертёж стёрли, оставив только точки
. Затем весь чертёж стёрли, оставив только точки  и
и  . Восстановите ромб по точкам
. Восстановите ромб по точкам  .
.
♦ Произвольную точку Р плоскости повернём вокруг точки А против часовой стрелки на угол 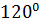 . Полученную точку
. Полученную точку 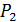 точно также повернём вокруг точки В и т. д. Середина отрезка
точно также повернём вокруг точки В и т. д. Середина отрезка  является вершиной А ромба.
является вершиной А ромба.
10.1. Существуют ли натуральные  для которых
для которых 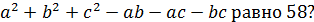
♦ Нет. Для натуральных  сумма
сумма 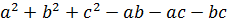 нечётна или делится на 4, а 58 чётно и не делится на 4.
нечётна или делится на 4, а 58 чётно и не делится на 4.
10.2. Найдите 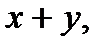 если
если 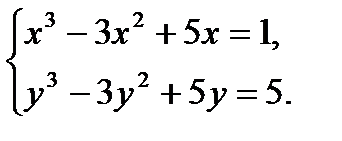
♦ Ответ. 2. Первое уравнение начинается со слагаемых 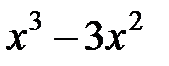 из формулы куба
из формулы куба 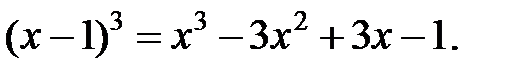 Это позволяет переписать систему в виде
Это позволяет переписать систему в виде
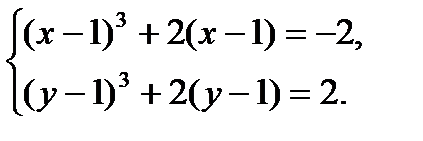
Складываем уравнения. Тогда
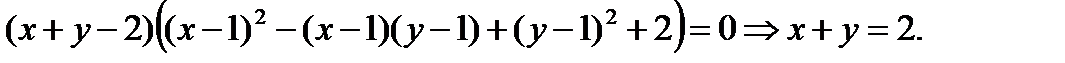
Замена 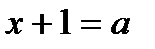 и
и 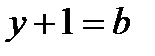 даёт другую запись этого же решения.
даёт другую запись этого же решения.
♦ Решение 2. Замена 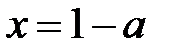 и
и 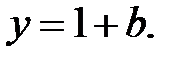 даёт
даёт 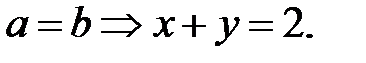
|
|
|
♦ Решение 3. Функция 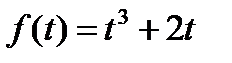 возрастающая и нечётная и
возрастающая и нечётная и
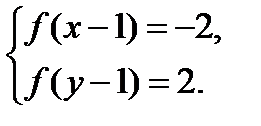
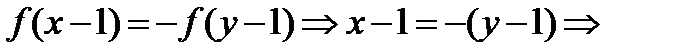

10.3. Окружности радиусов 13 и 35 с центрами  и
и  соответственно касаются внутренним образом в точке
соответственно касаются внутренним образом в точке 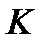 ;
; 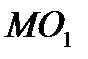 и
и 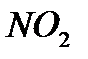 – параллельные радиусы этих окружностей, отложенные в одну полуплоскость относительно прямой
– параллельные радиусы этих окружностей, отложенные в одну полуплоскость относительно прямой 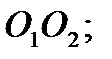
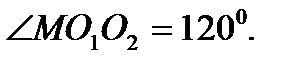 Докажите, что точки
Докажите, что точки 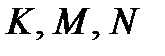 лежат на одной прямой.
лежат на одной прямой.
♦ Важно отметить, что точки 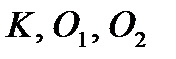 лежат на одной прямой. В равнобедренном треугольнике
лежат на одной прямой. В равнобедренном треугольнике  угол
угол 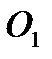 равен
равен 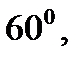 поэтому этот треугольник равносторонний и
поэтому этот треугольник равносторонний и 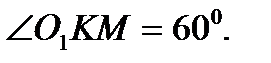 Так как радиусы параллельны, то
Так как радиусы параллельны, то  Вновь в равнобедренном треугольнике
Вновь в равнобедренном треугольнике 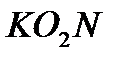 угол
угол  равен
равен 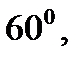 поэтому этот треугольник равносторонний и
поэтому этот треугольник равносторонний и 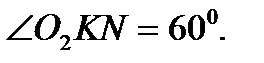 В одну полуплоскость от луча можно отложить только один угол, равный данному, поэтому лучи
В одну полуплоскость от луча можно отложить только один угол, равный данному, поэтому лучи  и
и  совпадают.
совпадают.
Другое решение; докажите, что 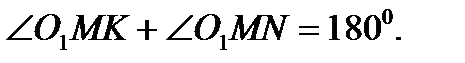
10.4. В квадрате со стороной 5 см размещено 126 точек. Докажите, что среди них существует 6 точек, которые лежат в круге радиуса 1 см.
♦ Квадрат 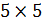 разобьём на 25 квадратиков
разобьём на 25 квадратиков  . Если в каждом квадратике окажется максимум пять точек, то всего получится 125 точек. А у нас их 126. Значит найдётся квадратик, в который попало не менее шести точек. Так как диагональ квадратика меньше 2, то этот квадратик можно полностью поместить в круг радиуса 1с центром в точке пересечения диагоналей. В этом круге в не менее шести точек.
. Если в каждом квадратике окажется максимум пять точек, то всего получится 125 точек. А у нас их 126. Значит найдётся квадратик, в который попало не менее шести точек. Так как диагональ квадратика меньше 2, то этот квадратик можно полностью поместить в круг радиуса 1с центром в точке пересечения диагоналей. В этом круге в не менее шести точек.
10.5. Три смеси составлены из трёх элементов А, В и С. В первую смесь входят только А и В в весовом отношении 3:5. Во вторую смесь входят только элементы В и С в весовом отношении 1:2. В третью смесь входят только А и С в весовом отношении 2:3 В каком отношении нужно взять эти смеси, чтобы во вновь полученной смеси элементы А, В и С содержались в весовом отношении 3:5:2?
♦ Ответ. 20:6:3.
| A | B | C | |
| x – вес первой смеси | 
| 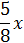
| |
| y – вес второй смеси | 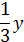
| 
| |
| z – вес третьей смеси | 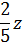
| 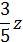
| |
| Всего | 
| 
| 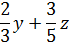
|

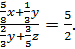
Из первого уравнения  , а из второго с учётом этого
, а из второго с учётом этого  .
.
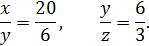

11.1. Какое наибольшее значение может принимать 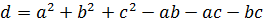 , если
, если  – двузначные натуральные числа и
– двузначные натуральные числа и 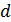 делится на 4?
делится на 4?
♦ Ответ:  . Так как сумма делится на 4, то
. Так как сумма делится на 4, то  – одной чётности. А так как они двузначные натуральные числа, то без ограничения общности можно взять
– одной чётности. А так как они двузначные натуральные числа, то без ограничения общности можно взять 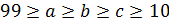 и
и
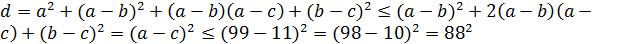 .
.
Значение  достигается, например, при
достигается, например, при 
11.2.Найдите все значения a, при каждом из которых система имеет единственное решение
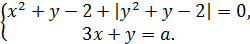
♦ Ответ: –8. При исследовании первого уравнения возникают два случая.
1) 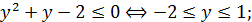
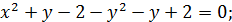
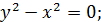
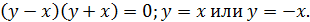
2) 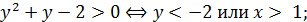


Изменяя a , двигаем прямую  параллельно прямой
параллельно прямой 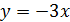 . Возникает единственная точка пересечения при
. Возникает единственная точка пересечения при 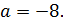
11.3. Множество М целых чисел (не всех) содержит вместе с любыми своими элементами их разность, Докажите, что М состоит из всех кратных некоторого  целого числа из этого же множества.
целого числа из этого же множества.
♦ 
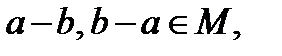
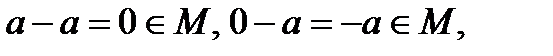 Заметим, что вместе с любым числом множеству М принадлежит и противоположное, поэтому в множестве М есть положительные числа и есть наименьшее положительное число с. Вычитая из модуля любого числа этого множества число с несколько раз обязательно получим в остатке 0. Если положительный остаток не равен нулю, то он меньше с и принадлежит М, а это противоречит выбору с. Вывод: все числа множества М делятся на с. Все числа, кратные с принадлежат множеству М.
Заметим, что вместе с любым числом множеству М принадлежит и противоположное, поэтому в множестве М есть положительные числа и есть наименьшее положительное число с. Вычитая из модуля любого числа этого множества число с несколько раз обязательно получим в остатке 0. Если положительный остаток не равен нулю, то он меньше с и принадлежит М, а это противоречит выбору с. Вывод: все числа множества М делятся на с. Все числа, кратные с принадлежат множеству М.
Сверх этого заметим, что


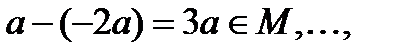


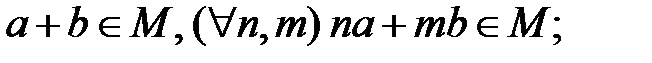
если в М найдутся взаимно простые числа, то  и
и 
11.4. Про квадратный трёхчлен  известно, что
известно, что  при
при 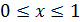 . Найдите наибольшее возможное значение
. Найдите наибольшее возможное значение 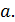
♦ Ответ. 8. Так как 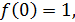
 то
то 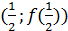 – вершина параболы и по условию
– вершина параболы и по условию 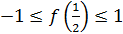 ,
,

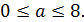
Так как 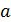 положительно, то ветви параболы направлены вверх и
положительно, то ветви параболы направлены вверх и  наименьшее значение функции
наименьшее значение функции 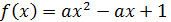 и оно удовлетворяет условиям задачи при наибольшем значении
и оно удовлетворяет условиям задачи при наибольшем значении 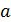 , равном 8. Всегда
, равном 8. Всегда
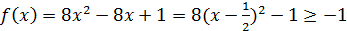 ;
;
а если  то
то 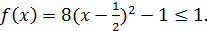
11.5. В окружность вписан правильный треугольник АВС, М – точка на дуге, соединяющей А и В. Докажите, что 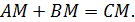
♦ Пусть при повороте против часовой стрелки на 60 градусов вокруг точки В точка М перейдёт в точку Р. (Вершины А, В и С перечисляем, двигаясь по часовой стрелке.) Тогда треугольник ВМА перешёл в ВРС;
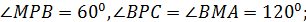

Точки 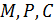 лежат на одной прямой, точка Р на отрезке МС и МР=МВ, СР=АМ.
лежат на одной прямой, точка Р на отрезке МС и МР=МВ, СР=АМ. 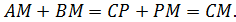
ЗАДАНИЯ ПРИМОРСКОЙ КРАЕВОЙ
Дата добавления: 2018-11-24; просмотров: 180; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
