Численное решение дифференциальных уравнений
Ранее было отмечено, что физические процессы удобно моделировать с помощью уравнений состояний, имеющих вид:
, 
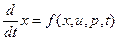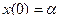
где x – n x 1-вектор состояний с начальным условием α; p – n x 1-вектор параметров;
u – q x 1-вектор управлений; f – n x 1-вектор-функция; t-переменная текущего времени.
Численное решение обыкновенных дифференциальных уравнений – важный этап работы системы цифрового управления.
Методы Рунге – Кутта
не требуют знания начальных состояний, и их можно применять к функциям с непрерывными производными. Простейшей схемой тина Рунге - Кутта является алгоритм с использованием первого члена разложения в ряд Тейлора. Для уравнения вида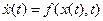 
раскладывая x(t+h) имеем:
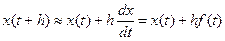
Этот алгоритм интегрирования называется также методом Эйлера.
Методы Рунге – Кутта
получил широкое распространение в технике цифрового моделирования. Основной принцип, реализуемый этим методом, заключается в решении уравнения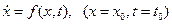 
путем вычисления производной x в точке ti и в двух или большем числе примыкающих точек в области ti (рис. 
Рис.
Методы Рунге – Кутта называется методом второго порядка, если его алгоритм учитывает все члены ряда Тейлора вплоть до слагаемого, пропорционально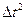 
включительно. Метод четвертого порядка охватывает все члены ряда вплоть до члена, пропорционального 
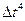, включительно и т.д. При методе более высокого порядка получается меньше ошибка вычисления на каждом шаге, но вычисление последовательных значений yi более трудоемко.
|
|
|
Достоинством метода Рунге – Кутта является возможность сравнительно просто контролировать точность результата в процессе вычислений. Величина интервала дискретизации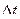 
может легко изменяться после любого цикла вычислений: на каждом шаге интегрирования значение yi, вычисленное с шагом 
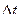, сравнивается со значением, вычисленным с шагом 
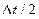(рис.), полученным после двух шагов интегрирования с половинным шагом. Если в результате сравнения:
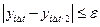
то за конечный берется результат, полученный при половинном шаге, т.е.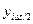 
. Если же это условие не выполняется, шаг интегрирования уменьшается еще в двое, т.е. берется шаг 
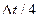. При таком способе контроля точности вычисления программист (или автомат) может уменьшать интервал 
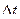до тех пор, пока не перестанет наблюдаться резкое изменение зависимой переменной с изменением интервала дискретизации 
.
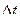Запишем в виде х = f (х, t), где параметр р входит в f, а функция u учтена явной зависимостью f от t. Разлагая х (t + h) в ряд Тейлора второго порядка относительно х (t), находим, что i-ю компоненту х (t + h) можно выразить:
|
|
|
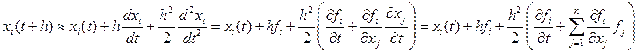Так следует вычислять, но хотим реализовать схему через вычисление правых частей в некоторых точках:
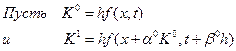
Найдем когда вычисления по желаемому алгоритму совпадут со следующим алгоритмом из рада Тейлора:
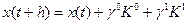
где γ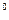 
и γ 
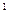
- константы.
Путем подстановки выражений, находим
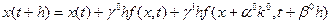
Раскладывая правую часть уравнения в ряд Тейлора относительно f(x, t), получаем i-ю компоненту:
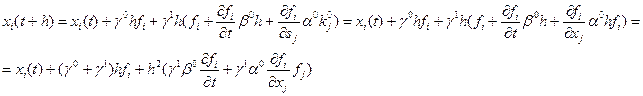Приравнивая соответствующие коэффициенты всех независимых производных f, получаем
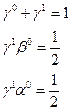
В этом случае уравнений меньше, чем неизвестных, и одним из возможных решений является
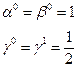
Подставляя эти константы, получаем алгоритм Рунге-Кутта второго порядка:
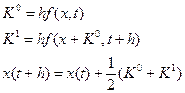
Путем аналогичных рассуждений можно показать, что алгоритм Рунге - Кутта четвертого порядка имеет вид
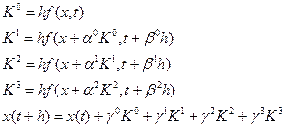
У процесса Рунге-Кутта 4-ого порядка следующее множество параметров:
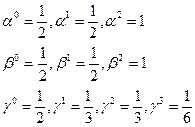
Ошибка для процесса Рунге-Кутта четвертого порядка определяется членом пятой степени в разложении Тейлора, но в общем случае ее трудно оценить.
Ориентировочно можно пользовать следующей таблицей ():
| Заданная допустимая ошибка |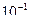 
| 
| 
| 
| 
|
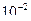
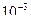
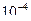
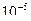
| Максимальный размер шага в процесс Рунге-Кутта первого порядка Максимальный размер шага в процессе Рунге-Кутта четвертого порядка | 0,445 1,644 | 0,141 1,037 | 0,0445 0,654 | 0,014 0,412 | 0,0014 0,164 |
Пример 1.9 Рассмотрим стандартную подпрограмму для численного интегрирования множества векторных дифференциальных уравнений вида:
|
|
|
, 
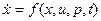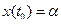
а. Используйте алгоритм Рунге-Кутта четвертого порядка.
б. Включите подпрограмму дифференциальных уравнений так, чтобы их можно было менять по желанию.
в. Обеспечьте возможность изменения числа уравнений.
г. Отладьте программу, проинтегрировав уравнения
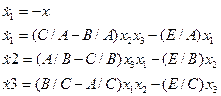
Эти уравнения описывают свободное движение вращающегося твердого тела. Здесь переменные Х1 Х2 Х3 - составляющие угловой скорости относительно главной оси, А, В и С – соответствующие главные моменты инерции и Е – показатель затухания.
Положите А=1, В=2, С=3, Е=0.2, Х1(to)=1, Х2(to)=1, Х3(to)=0. Используйте шаг h=0.1c. (Проверьте Х1(1,0)=0,9382328, Х2(1,0)=0,7705584, Х3(1,0)=0,2770832
//////////////////////////////////////////////////////////////////////////
// Файл: diff2.cpp
// Описание: Интегрирование системы дифф. ур.
// Зависимости: Стандарт С++
// Авторы: XXX
//////////////////////////////////////////////////////////////////////////
#include <math.h>
#include <stdio.h>
|
|
|
#include "Integrator.h"
/// Класс реализация модели (диф.ур.)
class CDiff2: public Integrator
{
protected:
double X[3]; ///< Переменные интегрирования
double t; ///< Время
public:
/// Конструктор
CDiff2()
{
Integrator::PreInitialize(3);
ODE_LEFT(0,X[0]); // Указание интегрируемых переменных
ODE_LEFT(1,X[1]);
ODE_LEFT(2,X[2]);
ODE_TIME(t); // Время
}
/// Реализация функции правых частей
bool Right()
{
try
{
double A = 1.;
double B = 2.;
double C = 3.;
double E = 0.2;
ODE_RIGHT(0) = (C/A-B/A)*XT(1)*XT(2) - (E/A)*XT(0); // Правые части
ODE_RIGHT(1) = (A/B-C/B)*XT(2)*XT(0) - (E/B)*XT(1);
ODE_RIGHT(2) = (B/C-A/C)*XT(0)*XT(1) - (E/C)*XT(2);
}
catch(...)
{
return false;
}
return true;
}
// Инициализация модели
void Initialize(double X1,double X2,double X3,double _t)
{
X[0] = X1;
X[1] = X2;
X[2] = X3;
t = _t;
}
// Опрос состояния
bool GetState(double& X1,double& X2,double& X3,double& _t) const
{
X1 = X[0];
X2 = X[1];
X3 = X[2];
_t = t;
return true;
}
bool Step()
{
return RK4Step();
}
};
// Испльзование CDiff2 и сохранение результатов в файл
void main()
{
FILE* fd; // Файловая переменная
fd = fopen("Result.txt","w"); // Отрытие файла для сохранения результатов
double X1,X2,X3,t; // Переменные состояния и время
CDiff2 diff1; // Класс - модель
X1 = 1.; // Начальные условия
X2 = 1.;
X3 = 0.;
t = 0.;
diff1.Initialize(X1,X2,X3,t); // Инициализация модели
diff1.SetStep(0.1); // Установка шага интегрирования
fprintf(fd,"%lf %lf %lf %lf\n",t,X1,X2,X3); // Сохранение состояния
while(t<=1.) // Условие окончания интегрирования
{
diff1.Step(); // Шаг
diff1.GetState(X1,X2,X3,t); // Опрос состояния
fprintf(fd,"%lf %lf %lf %lf\n",t,X1,X2,X3); // Сохранение состояния
}
fflush(fd); // Слив буферов потока
fclose(fd); // Закрытие файла
}
#ifndef __INTEGRATOR__
#define __INTEGRATOR__
//////////////////////////////////////////////////////////////////////////
// Файл: Integrator.h
// Описание: Класс для интегрирования обыкн. диф.ур. (ODE)
// Версия файла: 1.0.0.1
// Зависимости: Стандарт С++
// Авторы: Костюков В.В.
//////////////////////////////////////////////////////////////////////////
//
// Протокол изменений:
//
//
//
//////////////////////////////////////////////////////////////////////////
// Макрос связывает переменную вектора состояния P
// с N-ым элеменом массива интегрируемых переменных
// (Left Part of ODE)
#define ODE_LEFT(N,P) m_ppParam[N] = &(P)
// Макрос связывает (указывает) переменную времени Р
// (Left Part of ODE)
#define ODE_TIME(P) m_pTime = &(P)
// Макрос предоставляет доступ к вектору правых частей
// (Right Part of ODE)
#define ODE_RIGHT(N) m_pRight[N]
// Класс реализующий интегрирование системы диф.ур-ий (ODE)
// Для интегрирования уравнений необходимо:
// 1. Cоздать производные от Integrator класс,
// 2. Указать в конструкторе производного класса переменные интегрирования
// и параметр времени при помощи макросов ODE_LEFT, ODE_TIME
// 3. Реализовать виртуальную функцию Right,
// в теле функции определить вычисление правых частей,
// (испоользовать макрос ODE_RIGHT)
/// Класс для интегрирования обыкн. диф.ур.
class Integrator
{
private:
bool m_bInit; ///< Признак инициализации модели
double a[5]; ///< Коэфициенты РК-4
double *m_pDX; ///< ... для РК-4
protected:
double **m_ppParam; ///< Вектор указателей на интегрируемые параметры
double *m_pRight; ///< Вектор правых частей ( расчитывается в Right() )
double *m_pTime; ///< Параметр времени
double m_dT; ///< Шаг интегрирования
unsigned long m_nDim; ///< Размер вектора состояния
double *m_pXT; ///< ... для РК-4
public:
Integrator()
{
a[0] = 0.5;
a[1] = 0.5;
a[2] = 1.0;
a[3] = 1.0;
a[4] = 0.5;
m_dT = 0.01;
m_nDim = 0;
m_bInit = false;
}
~Integrator()
{
if(m_bInit)
{
delete[] m_ppParam;
delete[] m_pRight;
delete[] m_pXT;
delete[] m_pDX;
}
}
/// Инициализация интегратора
virtual bool PreInitialize(unsigned long nDim)
{
if(m_bInit) return false;
if(nDim>0) m_nDim = nDim;
else return false;
m_ppParam = new double*[m_nDim];
m_pRight = new double[m_nDim];
m_pXT = new double[m_nDim];
m_pDX = new double[m_nDim];
m_bInit = true;
return m_bInit;
}
/// Функция расчета правых частей ODE
virtual bool Right() {return true;}
/// Задать шаг интегрирования
bool SetStep(const double dT)
{
if( m_dT>0 )
{
m_dT = dT;
return true;
}
return false;
}
/// Опросить шага интегрирования
double GetStep() const
{
return m_dT;
}
/// Методы интегрирования
protected:
//////////////////////////////////////////////////////////////////////////
// Макроопределения для удобства записи алгоритмов интегрирования
#define X(i) *(m_ppParam[i])
#define DX(i) m_pDX[i]
#define XT(i) m_pXT[i]
#define DXT(i) m_pRight[i]
#define time *m_pTime
#define dt m_dT
#define N m_nDim
/// Шаг интегрирования методом Эйлера
bool EilerStep()
{
if(!m_bInit) return false;
try
{
unsigned int i;
if(!Right()) throw 0;
for(i = 0;i < N; i++)
{
X(i) += DXT(i)*dt;
}
time += dt;
}
catch(...)
{
return false;
}
return true;
}
/// Шаг интегрирования методом Рунге-Кутта 4-го порядка
bool RK4Step()
{
if(!m_bInit) return false;
try
{
double h = dt;
double t;
double b,c;
unsigned int i,j;
for(i = 0;i < N; i++)
{
DX(i) = 0;
XT(i) = X(i);
}
t = time;
for(j = 0;j < 4; j++)
{
if(!Right()) throw 0;
b=a[j+1];
c=a[j];
t=time+c*h;
for(i = 0;i < N; i++)
{
DX(i) += b*h*DXT(i)/3.;
XT(i) = X(i) + c*h*DXT(i);
}
}
for(i = 0;i < N; i++)
{
X(i) += DX(i);
}
time += dt;
}
catch(...)
{
return false;
}
return true;
}
// Очистка макроопределений
#undef X
#undef DX
#undef DXT
#undef time
#undef dt
////////////////////////////////////////////////////////////////////
};
#endif //__INTEGRATOR__
Дата добавления: 2018-11-24; просмотров: 210; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!