Численное дифференцирование и интегрирование
Цифровая вычислительная машина может обрабатывать непрерывный сигнал только как последовательность дискретных значений. Для получения оценок в предельных переходах при исчислении бесконечно малых необходимо непрерывное описание процессов, что можно реализовать через, например, полиномы. Полиномом в конечных разностях называется полиноминальная функция, которая проходит через заданное число конечных точек.
При рассмотрении конечно-разностных полиномов используются следующие обозначения:
Хr - значение Х в момент времени tr содержащееся в памяти машины,
Хr+n - значение Х в момент времени tr + nh, содержащееся в памяти машины,
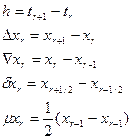
Операторы ∆, µ, δ, 
можно применять к выражениям последовательно. Пример конечно-разностного полинома:
где 
Соответствующий конечно-разностный полином третьей степени может быть записан в виде:
где 
Проверка показывает, что конечно-разностный полином P3 совпадает с непрерывным сигналом x в дискретных точках t = tr , t = tr + h , t = tr + 2h и t = tr + 3h
Дифференцирование
Конечно-разностную формулу дифференцирования можно получить дифференцированием соответствующего конечно-разностного полинома по t. Например, дифференцирование предыдущей формулы дает:
Полагая в t = tr получаем
Если исходить из других конечно-разностных полиномов, можно получить другие
конечно-разностные формулы дифференцирования.
|
|
|
Интегрирование
Конечно-разностные формулы для численного интегрирования можно получить аналогичным путем. Если рассмотрим, например, полином 2-ой степени:
где 
то формулу интегрирования можно легко получить аналитически:
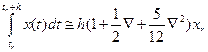
Чем больше членов содержит конечно-разностная схема, тем лучшим оказывается приближение к непрерывным данным и, следовательно, более точной формула интегрирования или дифференцирования. Первые отброшенные члены в этих выражениях обычно хорошо оценивают ошибку усечения.
Пример. Рассмотрим применение z-иреобразования для анализа динамических погрешностей на примере выбора вычислительного алгоритма дифференцирования входной величины, т. е. найдем вычислительный алгоритм, реализующий операцию дифференцирования с заданной динамической погрешностью 
для диапазона частот от 0 до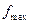 
входных сигналов.
Учитывая необходимость вычислений в реальном масштабе времени, т. е. учитывая и возможность использования значений входной функции лишь в предшествующие моменты времени, и используя, например, второй полином Ньютона, можем записать формулы численного дифференцирования в следующем виде:
для п =2
|
|
|
(1.2)
для п =3
(1.3)
для п =4
(1.4)
где Т—период квантования входных данных; 
, 
, 
,… 
— значения входной величины в моменты времени k , k—1, k—2, k—4; n— степень интер-ующего полинома.
Применяя z-преобразование к (1.2), в частности используя свойство z-преобразование для последовательности запаздывающих входных данных [12], получим дли п ==2
Учитывая, что 
, определим передаточную характеристику программы дифференцирования:
О следовательно, АЧХ
и ФЧХ
где 
; 
Аналогично получим передаточную характеристику, АЧХ и ФЧХ для программ дифференцирования по (1.3):
где 
, и по (1.4):
где 
Вычислив зависимости АЧХ и ФЧХ для ряда значений периода квантования Т в полосе частот входных сигналов, можно решить, какой из алгоритмов удовлетворяет условию обеспечения максимально допустимой динамической погрешности (амплитудной и фазовой) при минимальной сложности вычислений и максимальном периоде квантования. При этом должно обеспечиваться условие устойчивости (сходимости) алгоритма. Последнее проверяется моделированием работы выбранных числовых алгоритмов на универсальной ЭВМ или оценкой погрешности интерполяционного метода по разности точного решения и полученной вычислительной формулы.
|
|
|
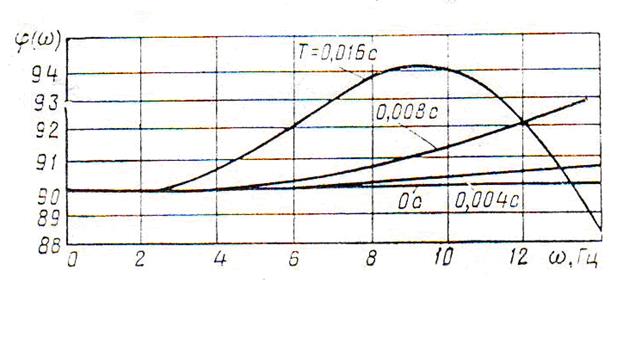
На рис. 1.9, а, бсоответственно-приведены зависимости 
и 
для вычислительной формулы (1.3) в диапазоне частот от 0 до 15 Гц при Т=0,004 с, Г = 0,008 с и Г= = 0,016 с.
Отметим, что для ИУВС,. работающих в реальном масштабе времени, анализ динамических погрешностей алгоритмов позволяет определить ряд важнейших технических характеристик ИУВС: требуемое быстродействие, информационные объемы оперативной и постоянной памяти, систему команд, вычислительные алгоритмы, циклограммы обработки входных данных.
Дата добавления: 2018-11-24; просмотров: 240; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!