Переходная матрица состояния и решение уравнения состояния
Основное преимущество линейных дифференциальных уравнений состоит в том, что можно указать замкнутую форму решения таких уравнений.
Решение матричного дифференциального уравнения (1.26), используемое в дальнейшем для исследования динамических характеристик систем, можно получить исходя из свойств матричной показательной функции вида
 (1.30)
(1.30)
получившей название переходной матрицы состояния. Переходная матрица состояния определяется как обратное преобразование Лапласа сомножителя в передаточной функции системы:
 (1.31)
(1.31)
Рассмотрим основные свойства функции (1.30):
1)  (1.32 а)
(1.32 а)
2)  (1.32 б)
(1.32 б)
3)  (1.32 в)
(1.32 в)
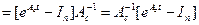 для
для  (1.32 г)
(1.32 г)
4) 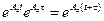 (1.32 д)
(1.32 д)
5)  (1.32 е)
(1.32 е)
6)  , для любых
, для любых 
 (1.32 ж)
(1.32 ж)
|
|
|
Пусть в некоторый момент времени t = tо на вход системы приложено воздействие u(t), представляющее собой кусочно-непрерывную функцию времени, тогда решение х(t) уравнения (1.26а) можно представить в виде
 (1.33)
(1.33)
где х(t0) - значение переменной состояния в некоторый начальный момент времени t = t0.
В частном случае, если t0 = 0, выражение (1.33) упрощается и принимает вид
 (1.34)
(1.34)
Доказывается, что выражение (1.33) является решением уравнения (1.26) простой подстановкой (1.33) в (1.26) с дифференцированием в левой и правой части.
В решениях дифференциальных уравнений принято выделять 2 движения:
- Собственное движение, определяемое как движение обусловленное ненулевыми начальными значениями, независимое движение от управляющих процессов (хотя может они и вывели ранее систему в это положение). Это 1-ое слагаемое в решении линейных дифференциальных уравнений (является для линейного решения ) состоит из переходной матрицы умноженной на значение переменной в начальный момент времени.
- вынужденное движение, определяемое как составляющее движение под действием управляющего входного сигнала. Это интегральное слагаемое в решении, которое в разных дисциплинах имеет множество названий ( например интеграл Дюамеля, интеграл свертки и т.д…).
|
|
|
Отметим, что в такой форме (1.33) записывается решение только для линейных систем, но понятие «собственное» и «вынужденное» движения есть и для нелинейных систем.
Важнейшим вопросом, связанным с решением дифференциальных уравнений является вопрос нахождения решений уравнений, когда может наблюдаться качественное изменение решения дифференциальных уравнений и именно когда при изменении параметров входящих в описании системы, вместо затухающего собственного движения может наблюдаться расходящееся движение, и тогда в общем решении дифференциальных уравнений вклад собственного движения огромен, а движение обусловленное управляющим воздействием мало, т.е. объект практически не реагирует на входной сигнал, а наблюдаем только собственное, как правило, ненужное нам движение объекта.
Системы с параметрами, при которых имеем затухающее собственное движение называются устойчивыми.
В точностных исследованиях систем вопросы обеспечения устойчивости – это очень важный раздел, и вы его изучали в курсе ТАУ, а непосредственно в рамках данного курса мы его внимательно не рассматриваем, хотя кому то придется выяснять при моделировании, что за причины расходящихся движений системы: собственная устойчивость исходной САУ или вопросы связанные с неправильными операциями дискретизации процессов по времени и т.д…
|
|
|
Пример 1.
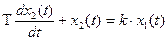 дифференциальное уравнение 1-го порядка
дифференциальное уравнение 1-го порядка
Начальные значения:
входной сигнал: 
выходной сигнал: 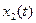
Т, k- известные числа, характеристики звена;
k – Статический коэффициент усиления.
Начальные значения:
 /известное число/
/известное число/

Звено описывается с помощью дифференциального уравнения 1-го порядка (апериодичное звено).
Т – const – постоянная времени;
 - входной сигнал;
- входной сигнал;
 - выходной сигнал;
- выходной сигнал;
k – статический коэффициент усиления;

 - единичная ступенька
- единичная ступенька
Движение системы (звена) мы всегда рассматриваем, состоящим из двух составляющих: из свободного движения (движения, обусловленного внутренними свойствами звена и обусловленного ненулевыми начальными условиями). В математике свободное движение ищется как общее решение однородного уравнения (без правой части дифференциального уравнения (т.е. входной сигнал=0)).
|
|
|
Записываем характеристическое уравнение

Собственное движение: 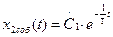




 отсюда :
отсюда : 
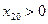 т.е.
т.е. 

 t
t

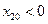
 _ ______
_ ______
≈(3  4) Т
4) Т
Собственное движение – это движение, которое в СУ, как правило, должно с течением времени сходится к нулю. Такие системы – устойчивые. Исследования устойчивости линейных систем – это исследования собственного движения.
Вынужденная составляющая – то движение, которое обусловлено внешними воздействиями на систему.
Вынужденное движение состоит из двух составляющих:
1 – частное решение неоднородного уравнения;
2 – общее решение однородного уравнения.
Вынужденное движение ищется при нулевых начальных условиях.
Найдем вынужденное движение:
а) Частное решение. Для того, чтобы решать неоднородные уравнения разработана специальная методика по решению дифференциальных уравнений со специальной правой частью. Если входной сигнал – постоянная величина, то и частное решение есть постоянная. Если входной сигнал гармонический – частное решение в виде гармонического сигнала (такой же частоты). Если входной сигнал экспонента – то в виде экспонент и т. д. Для нашего примера:
x2част(t)=A=const
Подставляем в исходное уравнение:
T 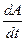 +A=k
+A=k  1
1
Отсюда: A=k
x2част(t)=k (k-известное число)
б) Общее решение уже находили
x2одн(t)=С1 е-t/T - однородное
x2вынужд.(t)=x2част(t)+ x2одн(t)=k+С1е-t/T
при нулевых начальных условиях
x2вынужд.(0)= k+С1е-0/T=0
отсюда:
k+С1=0  С1=-k
С1=-k
x2вынужд.(t)=k-kе-t/T=k(1-e-t/T) –при единичном входном сигнале эта переходная функция


Выходной сигнал при нулевых начальных условиях, т.е. обусловлено вынужденной составляющей при единичной функции на входе, называется переходной функцией системы.
! Пример 2.
Входной сигнал - гармоничное воздействие
Т  +х2(t )=k sin
+х2(t )=k sin  t
t 
T, k,  - известные значения;
- известные значения;  может принимать любые значения, но предполагается, что для конкретного данного решения системы
может принимать любые значения, но предполагается, что для конкретного данного решения системы  - постоянно.
- постоянно.
х2(t=0)=x20.
Решение будет состоять из:
1) Решение однородного уравнения х2соб(t)=х20е-t/T (аналагично примеру1)
2) Вынужденное:
частное решение: х2част(t)=C1sin  t+C2cos
t+C2cos  t;
t;
Подставим в частное решение в дифференциальном уравнении, найдем С1, С2
Т(С1cos  t*
t*  (-C2)sin
(-C2)sin  t*
t*  )+C1sin
)+C1sin  t+C2cos
t+C2cos  t=ksin
t=ksin  t
t
Приравниваем левую и правую части:
TC1cos  t*
t*  +C2cos
+C2cos  t=0
t=0
-C2Tsin  t*
t*  +C1sin
+C1sin  t=ksin
t=ksin  t
t
ТС1  +C2=0
+C2=0  C2=-ТС1
C2=-ТС1 
-ТС2  +C1=k
+C1=k
C1=k+Т  (-ТС1
(-ТС1  )
)
C1(T2  2+1)=k
2+1)=k  C1=
C1= 
C2=- 

A (  ) - амплитудно-частотная характеристика системы (звена) (в данном случае - апериодическое звено);
) - амплитудно-частотная характеристика системы (звена) (в данном случае - апериодическое звено);
φ (  )=arctg (-
)=arctg (-  ) - фазо-частотная характеристика (в данном случае - это ФЧХ апериодического звена);
) - фазо-частотная характеристика (в данном случае - это ФЧХ апериодического звена);
вынужденное движение состоит из следующего:
x2вынужд.(t)=A(  )sin(
)sin(  t+ φ (
t+ φ (  ))+C1∙e-t/T
))+C1∙e-t/T
подставляем нулевые условия: t=0
А(  )sin (φ (
)sin (φ (  ))+C 1 =0
))+C 1 =0
C1=-A(  )sin(φ(
)sin(φ(  ))
))
x2вынужд.(t)=A(  )sin(
)sin(  t+φ(
t+φ(  ))- A(
))- A(  )sin(φ(
)sin(φ(  )) e-t/T
)) e-t/T
x2(t)=x20e-t/T + A(  )[sin(
)[sin(  t+φ(
t+φ(  ))-sin(φ(
))-sin(φ(  )) e-t/T] – вых. сигнал
)) e-t/T] – вых. сигнал


Когда на систему действует несколько воздействий, то у линейных систем есть свойство суперпозиции состоящее в том, что эффект от действия суммы воздействий можно рассчитать как аддитивную сумму от каждого из воздействий в отдельности и тогда решение будет в виде:

Пример 3.
Рассмотрим упрощенную модель задачи управления самолетом по углу рыскания в горизонтальном полете. Предположим, что порывы ветра, создавая момент wв(t), разворачивают самолет относительно требуемого направления и требуется корректировать ошибки рыскания с помощью соответствующих отклонений руля.

Рис. Схематическая модель динамики самолета
Осевая линия самолета
Расчетное направление
Ось рыскания
Руль
Графически это модель изображена на рис. 3. Здесь  - ошибка рыскания, а
- ошибка рыскания, а  - отклонение руля. Ось рыскания, проходящая через центр тяжести, вертикальна. Самолет имеет относительно этой оси момент инерции J, восстанавливающий момент пропорционален отклонению руля.
- отклонение руля. Ось рыскания, проходящая через центр тяжести, вертикальна. Самолет имеет относительно этой оси момент инерции J, восстанавливающий момент пропорционален отклонению руля.
Второй закон Ньютона относительно вертикальной оси:
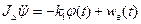
где k1 – коэффициент пропорциональности между отклонением руля и восстанавливающим моментом (k1 >0)
wв(t) – момент, вызываемый порывами ветра.
Разделив уравнение на J и обозначая  , имеем:
, имеем:
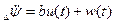
Полученное дифференциальное уравнение имеет второй порядок. Поэтому кроме знания функций u (t ) и w (t ) для нахождения его решения при 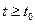 требуется задать два начальных условий:
требуется задать два начальных условий:  начальную ошибку по углу рыскания и
начальную ошибку по углу рыскания и 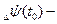 начальную ошибку по скорости изменения угла рыскания.
начальную ошибку по скорости изменения угла рыскания.
Вводя переменные  и
и  запишем уравнение системы в следующем виде:
запишем уравнение системы в следующем виде:
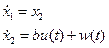
Или, что то же самое:

где  - вектор состояния, состоящий из двух физических величин: ошибки по углу рыскания и ошибки по скорости изменения угла рыскания.
- вектор состояния, состоящий из двух физических величин: ошибки по углу рыскания и ошибки по скорости изменения угла рыскания.
Сравнивая полученный результат с уравнением (1.26) можно видеть, что в рассматриваемом случае:

а возмущение w (t ) и управление u (t ) являются скалярами.
Предполагая, что ошибки по углу рыскания и скорости его изменения можно измерять на борту самолета с помощью инерциальной системы, уравнение измерения можно записать в виде:

где  - вектор измерения
- вектор измерения
 - вектор ошибки измерения, т.е. v 1 (t ) – ошибка измерения угла рыскания, а v 2 (t ) – ошибка измерения скорости изменения угла рыскания.
- вектор ошибки измерения, т.е. v 1 (t ) – ошибка измерения угла рыскания, а v 2 (t ) – ошибка измерения скорости изменения угла рыскания.
Дата добавления: 2018-11-24; просмотров: 836; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
