Динамические характеристики системы в тактовые моменты времени

⇐ ПредыдущаяСтр 5 из 7Следующая ⇒

Цифровое (микропроцессорное) управление - это управление, при котором данные измерений и сигналы управления, формируемые вычислительной машиной, поступают только в виде дискретных значений с заранее определенным временным интервалом следования. Этот временной интервал Т называется периодом дискретизации (квантования). При этом значение сигнала после аналого-цифрового преобразования и до выхода из вычислительной машины представляется в виде машинного слова - дискретного сигнала, который в двоичной системе кодирует несколькими разрядами значение исходного аналогового сигнала в определенные тактовые моменты времени iT.

В простых регуляторах, таких, как, например, ПИД (пропорционально-интегрально-дифференциальный)-регулятор, период квантования Т определяется затратами времени на аналого-цифровое и цифроаналоговое преобразования сигналов. В тех случаях, когда объем и сложность вычислений по задачам управления возрастают, требуя применения микропроцессора либо вычислительной машины под периодом квантования (дискретизации) обычно понимается время, затрачиваемое на выполнение требуемых вычислений, а затраты времени на аналого-цифровое и цифроаналоговое преобразования либо не учитываются совсем, либо оцениваются приближенно.

T u[i] u(t) x(t)

ЦАП Фиксатор Объект управления

ЦВМ

АЦП T x(t)

x[i]

a )

T u[i] ЦАП u(t) Объект управления x(t)

Объект управления

Процессор Интерфейс

АЦП Выборка и хранение

информации

x[i]

б)

Рис 1.4 Функциональная схема системы цифрового управления. (а) обобщенная схема системы цифрового управления. (6) Схема цифрового управления с фиксатором (экстраполятором) нулевого порядка. ЦАП - цифроаналоговый прео6разователь; АЦП аналого-цифровой прео6разователь.

С выхода объекта управления через аналого-цифровой преобразователь (АЦП) в вычислительную машину поступает либо сигнал x[t] = х(iT) с интервалом времени Т. Микропроцессор обрабатывает эти сигналы и вычисляет управляющее воздействие, значения которого через каждый интервал времени T после цифроаналогового преобразования возобновляются в экстраполяторе (фиксаторе). Затем управляющее воздействие передается на объект управления.

Под экстраполятором понимается схема преобразования дискретного сигнала в непрерывный сигнал. Подобный экстраполятор обычно называется фиксатором нулевого порядка, если его выход ной сигнал поддерживается на интервале времени Т постоянным (рис. 1.4 а). В отличие от такого фиксатора в экстраполяторе первого порядка (рис. 1.4 б) осуществляется обобщение дискретных данных на интервале времени т по предыдущей и теку шей выборкам. Очевидно, что в зависимости от типа экстраполятора меняется и дискретная модель объекта управления.

u(t)

u[2] u[2]

u[0] u[0]

u[1] u[1]

0 T 2T t a) 0 T 2T 3T t

u(t)

u[0]

u[2]

u[1]

0 T 2T 3T t

б)

Рис. 1.5 Характеристики сигналов на входе и выходе экстраполятора нулевого (а) и первого (б) порядков.

На современном уровне развития микропроцессорной технологии наибольшее распространение в практике получил фиксатор нулевого порядка, где удается обеспечить малое Т.

В этом случае цифровой сигнал хранится в памяти накопителя (триггерного типа) на протяжении периода Т, и через цифроаналоговый преобразователь непрерывно, в течение времени Т выдается на объект управления постоянный по величине аналоговый сигнал (рис. 1.5 б). Такая организация работы экстраполятора требует периодического, через каждый интервал времени Т обновления содержимого памяти.

Аналого-цифровые преобразователи осуществляют дискретную выборку данных из входного аналогового сигнала и выполняют роль интерфейса между объектом управления и вычислительной машиной (рис. 1.4). Рассмотрим теперь математическую модель в виде уравнения состояния, дискретной системы управления аналоговым объектом с учетом использования фиксатора нулевого порядка.

Для этого установим взаимосвязь между сигналами u[i] и х[i], воспользовавшись схемой, где входная часть фиксатора нулевого порядка представляет собой дискретизатор и аналого-цифровой преобразователь, а выходная часть цифроаналоговый преобразователь.

Пусть u[i] - дискретный сигнал, тогда непрерывный, или аналоговый, сигнал u[t], поступающий на объект управления и являющийся выходным сигналом фиксатора нулевого порядка, удовлетворяет соотношению (см. рис. 1.6).

Обозначим переменную состояния объекта управления и выходную переменную при t = iT через х [i] соответственно, причем

u[i] Фиксатор u(t) Объект x(t)

нулевого порядка управления x[i]

Рис. 1.6 Функциональная схема взаимосвязи дискретных и непрерывных сигналов в системе цифрового управления

x(t)

x[1] x[2]

x[3]

x[0]

u[1] u[2]

u[0]

0 T 2T 3T t

Рис. 1.7 Значения переменных в дискретные моменты времени.

с учетом этого можно записать

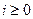, (1.39 а)

(1.39 б)

где

, , (1.39 в)

Решение уравнения состояния по аналогии с выражением (1.33) и с учетом того, что t₀ = iT, t = (i + 1) Т, будет иметь вид

(1.40)

Очевидно, что если на каждом временном интервале интегрирования Т u(t) представляет собой постоянную величину u[i], то, пре образуя переменную интегрирования δ= (i + 1)Т - т, получаем тождественность выражений (1.40) и (1.39 б). При этом выражение (1.39 б) получается в результате прямой дискретизации выражения (1.26 б).

Уравнения (1.39) называются уравнением состояния и уравнением выхода дискретной системы. Эти уравнения определяют динамические характеристики системы в тактовые моменты времени и графически могут быть представлены в виде структурной схемы, где оператор Z 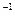- оператор запаздывания на один такт (период), а матрица А, определяющая переход переменной состояния x[i] в x[i + 1], - матрица перехода состояния.

Решение уравнения (1.39 б) легко получить из следующей вектор ной рекуррентной формулы:

(1.41)

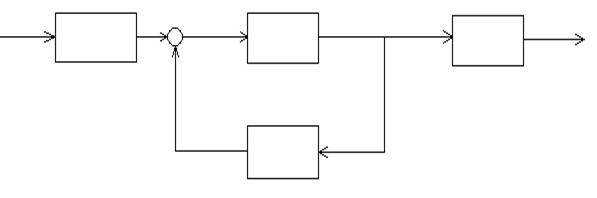u[i] + x[i+1] x[i] y[i]

b z^-1I_n c

Рис. 1.8 Структурная схема дискретной системы в пространстве состояний

Уравнение (1.39) удобно использовать при моделировании непрерывной системы.

В этом случае период квантования Т выбирается достаточно малым, с тем, чтобы на периоде Т входную величину u(t) в выражении (1.26) считать постоянной. Значения х[i] определяются численным методом по рекуррентной формуле (1.41) с помощью соотношений (1.30) и (1.32 в) для определения матричной показательной функции и соответствующих интегралов.

Многовходные физические системы можно описать системой линейных разностных уравнений первого порядка:

(2.30)

для k=0,1… В уравнении (2.30) векторы x, ω, и u представляют собой собственно векторы состояния, возмущения и управления системы. Однако здесь они определены только в дискретные моменты времени.

Назовем матрицу размера переходной матрицей состояния, матрицу размера - переходной матрицей возмущения и матрицу размера - переходной матрицей управления. Предположим, что k=0 соответствует фиксированному начальному времени t ₀ и начальное состояние x(0) известно.

Последовательность называется возмущающей

последовательностью, а - управляющей последовательностью. Энная эти две последовательности и вектор x (0), можно с использованием уравнения (2-30) вычислить последовательность состояния .

Пока будем полагать, что возмущающая и управляющая последовательности произвольны.

Допустим, что измерительную систему можно описать уравнением (2-2), но измерения проводятся только в те же дискретные моменты времени, в какие определено состояние системы (2.30). Поэтому в качестве модели системы измерения выберемся уравнение:

(2.31)

для k=0,1,…, где z и v – m-векторы, а Н – матрица размера . Заметим, что аргумент (k+1) в уравнении (2.31) можно изменить на k.

Последовательность 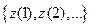называется последовательностью измерения или выходной последовательностью системы, а называется последовательностью ошибок измерения.

Описание системы вида (2.30), (2.31) называется дискретной линейной системой. Структурная схема модели приведена на рис. 2-7, где блок БЗ соответствует блоку хранения или задержки значения x из предыдущего вычислительного цикла для использования его в последующем цикле. Иными словами, после того как состояние x(k) вычислено, его следует хранить до момента k+1, чтобы использовать при определении x(k+1).

Рис. Структурная схема дискретной линейной системы

Наиболее часто такое описание системы встречается при дискретизации непрерывной линейной системы. Такая формулировка является естественной, если, например, из соображений экономии измерения проводятся только в дискретные моменты времени. Теперь покажем, что уравнения (2.30) и (2.31) являются дискретными аналогами уравнений (2.1) и (2.2).

Дискретизованная модель

Предположим, что векторы возмущения и управления системы (2-1) являются кусочно-постоянными функциями времени, причем оба они изменяют свои значения в одни и те же моменты времени. Далее предположим, что измерения проводятся в те же моменты времени.

Рассмотрим интервал времени для некоторого k=0,1,… Предположим, что x(t_k) известно, и для

Тогда из решения непрерывного уравнения следует, что:

(2.32)

Обозначая

(2.33)

уравнение (2.32) можно переписать в виде:

Полученное соотношение совпадает с уравнением (2.30).

В каждый момент t =t_k ₊₁ , k =0,1,… уравнение (2.2) принимает вид:

или, что то же самое:

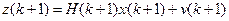
Это уравнение аналогично уравнению (2.31).

Заметим, что в последних двух равенствах из (2.33) для вычисления и необходимо иметь переходную матрицу состояния в виде, в котором ее первый аргумент является постоянным, а второй – переменным.

Пример 4. Применим изложенную методику для получения дискретной модели стационарной системы второго порядка из примера 3. Для простаты предположим, что дискретные моменты отсчета отстоят друг от друга на постоянные промежутки времени Т. Тогда k+1 соответствует моменту времени (k+1)T, а k – моменту kT.

Так как:

то Fⁿ=0 для всех . Следовательно, переходная матрица состояния

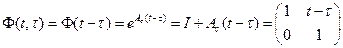
Поэтому

Тогда, согласно уравнению (2.33):

Аналогично

Следовательно, динамика системы описывается уравнением:

Соответствующее уравнение модели измерения:

Методика получения дискретной модели из непрерывной приведена выше. Теперь составим методику обратного перехода. Для этого обозначим дискретные моменты времени k и k+1 через t и t+∆t соответственно, где ∆t>0.

Затем, разлагая в ряд Тейлора по степеням ∆t, получаем:

где - матрица размера , все элементы которого имеют порядок 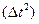и выше.

Поскольку и , имеем:

(2.34)

Из четвертого равенства в (2.33) ясно, что

(2.35)

Аналогично

(2.36)

Заменяя в уравнении (2.30) k и k+1 на t и t+∆t соответственно, имеем:

Подставляя в это соотношение уравнение (2.34)-(2.36) и группируя члены, получаем:

Перенося x(t) в левую часть уравнения, деля обе части на ∆t и переходя к пределу при , для получаем уравнение

совпадающее с уравнением (2.1). Уравнение

при принимает вид:

Вычислительные методы

Поскольку назначением математической модели является предсказание реакции системы на выбранные входные сигналы, необходимо сформировать начальные условия для уравнения модели, и решать дифференциальные уравнения.

Наиболее распространенными оказались методы Рунге-Кутта для решения дифференциальных уравнений.

Но не всегда целесообразно использовать метод Рунге-Кутта высокого порядка. Для интегрирования уравнений в бортовых вычислителях хорошо зарекомендовали метод Рунге-Кутта первого порядка (метод Эйлера), особенно если шаг по времени мал, а сигналы медленны.

Дата добавления: 2018-11-24; просмотров: 268; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 Следующая ⇒

Мы поможем в написании ваших работ!