Математическое описание объектов управления
Систему автоматического управления условно можно представить состоящей из двух частей (рис. 1.1): из объекта управления (ОУ) и управляющего устройства (УУ).
Под объектом управления применительно к инженерным задачам подразумевается любой процесс /техническое устройство/, координатой x(t) на выходе которого нужно управлять.
Управляющее устройство включает все входящие в контур системы управления элементы, используемые с целью реализации процесса управления. На вход системы управления подается как правило задающее воздействие g (t), определяемое как желаемый вид процесса x (t). Управляющее устройство на основании информации о процессе g (t) и измерениях x (t), и на основании информации о возмущении f(t) «рассчитывает» управление u(t), с помощью которого воздействует на объект с целью поставить процесс x(t) в соответствие сигналу g (t) в рамках некоторого формального описания этого соответствия. Например, обеспечивая минимальное значение среднего квадрата ошибки:
В общем случае ОУ является многомерным (рис. 1.2,а и б), имеет 
управляемых процессов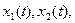 
.. 
; m входных воздействий (управлений) 
.. 
; k внешних возмущений 
Математическая запись физических законов, определяющих свойства непрерывного объекта, в большинстве случаев приводит к системе нелинейных дифференциальных уравнений, связывающих выходные и входные процессы и их производные. Эта система может иметь весьма сложную форму и, например, в случае объекта с независимыми выходными процессами быть представлена соотношениями вида:
|
|
|
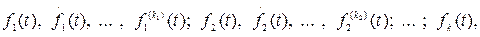
=1, 2, … . (1.1)
При =1 объект называют одномерным. Если функции 
являются линейными относительно управляемых и управляющих процессов и их производных, то объект называют линейным по управлению; аналогично определяется линейность по возмущению.
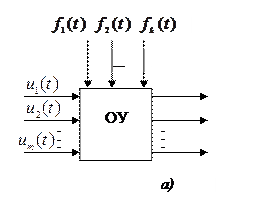
Рис. 1.2
Математическая модель (1.1) в современной теории систем получила ограниченное распространение. Гораздо чаще дифференциальных уравнений (1.1), из которых -е имеет порядок 
, представляют в виде системы из 
дифференциальных уравнений первого порядка, каждое из которых разрешено относительно производной. С этой целью в рассмотрение вводят 
новых переменных 
которые подбирают таким образом, чтобы систему (1.1) оказалось возможным представить в форме:
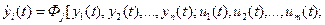
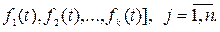(1.2)
Эту систему называют нормальной формой Коши. Выходные процессы ОУ выражаются через введенные переменные — переменные состояния — соотношениями вида 
(1.3)
где стоящие в правой части функции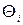 
являются в общем случае нелинейными. Система уравнений (1.2) должна быть эквивалентна исходной системе (1.1) в том смысле, что по решению (1.2) можно однозначно устанавливать решение системы (1.1). Совокупность уравнений (1.2), (1.З) часто называют уравнениями состояния.
|
|
|
Переход к системе в форме (1.2) необходим, поскольку установившая компьютерная реализация решения основана на форме уравнения (1.2).
Переход от системы уравнений в форме (1.1) к уравнениям состояния не является однозначным, т. е. может быть осуществлен различными путями. Одной и той же
исходной системе уравнений может соответствовать несколько систем в форме Коши в зависимости от способа определения переменных состояния. Универсальных рекомендаций для перехода, обеспечивающих преобразование самых произвольных нелинейных уравнений (1.1) в форму (1.2), (1.З), в настоящее время нет. Рассмотрим наиболее распространенные подходы.
1. Достаточно просто уравнения состояния находятся, когда уравнения (1.1) являются линейными с постоянными коэффициентами — стационарными. Положим, что ОУ одномерный с одним управлением 
и одним возмущением 
. Общее описание такого объекта сводится к линейному уравнению -гo порядка с постоянными коэффициентами
|
|
|
в составе которого 
с тем, чтобы уравнение не теряло свойств уравнения -го порядка, а часть остальных коэффициентов могла равняться нулю. Эти уравнения с использованием оператора дифференцирования 
удобно переписать в операторной форме
(1.4)
где
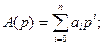
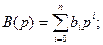
Формально (1.4) можно разрешить относительно x(t):
Сомножители 
часто называемые операторами объекта по управлению и возмущению соответственно, разложим на элементарные слагаемые, воспользовавшись правилами формальных операций над дробно-рациональными функциями:
(1.5)
Величины 
, 
являются корнями характеристического уравнения
которое формируется на основании полинома А(р) путем замены оператора дифференцирования р комплексной переменной s. Для простоты предположим, что это уравнение не имеет кратных корней, однако корни, как и остальные входящие в (1.5) величины, определяемые по правилам
(1.7)
могут быть комплексными .С учетом (1.5) уравнение (1.4) приобретает структуру
. (1.8)
|
|
|
Введем переменные состояния 
, 
, использовав определения
Учитывая смысл символа р, эти соотношения можем переписать в форме дифференциальных уравнений первого порядка, разрешенных относительно производных,
, i= 
. (1.9)
Выходная величина объекта выразится через переменные состояния и внешние воздействия:
. (1.10)
Соотношения (1.9), (1.10) и будут уравнениями состояния линейного стационарного объекта. Их удобно переписать в матрично-векторной форме. С этой целью введем обозначения : 
- вектор состояния, компонентами которого являются переменные состояния; 
- диагональная матрица, элементы главной диагонали которой равны корням характеристического уравнения, а остальные элементы – нули; 
, 
, 
- n-мерные векторы с указанными элементами; верхний индекс «т» - здесь и далее символ транспортирования. Тогда уравнения состояния переписываются в форме
(1.11)
2. Наиболее распространенный способ перехода, основанный на введении переменных состояния по правилу [12]
; 
; 
; ...; 
,
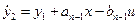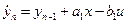(1.12)
где для упрощения записей принято f(t) = 0, приводит к следующей матрично-векторной форме уравнения состояния:
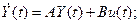
. (1.13)
Здесь А – квадратная n-матрица; В, С – n-мерные векторы; d – скаляр, определяемые соотношениями
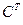= [1/ 
, 0, 0, ..., 0]; d = 
/ ;
(1.14)
В (1.11), (1.13) переменные состояния имеют различный смысл. Однако с помощью специальной замены переменных можно осуществить переход от одного уравнения к другому.
Пример. 1.1. Используя метод разложения на элементарные дроби, найти уравнения состояния в форме (1.11) для объекта управления, описываемого уравнением 
.
В данном случае 
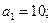
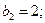
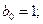характеристическое уравнение 
имеет корни 
. Из вышеприведенных соотношений следует
; 
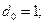
Следовательно, уравнения состояния имеют вид
Учитывая, что в соответствии c первыми двумя уравнениями этой системы 
и подставляя их значения в третье уравнение, приходим к исходному уравнению объекта. Этот результат свидетельствует об эквивалентности обеих форм математического описания объекта.
Пример. 1.2. Уравнение объекта из примера 1.1. представить в форме (1.13). В соответствии с (1.14) находим 
; 
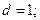
и из (1.13) следует искомые уравнения состояния
.
Разрешить первые два уравнения системы относительно 
, установим 
. Если этот результат подставим в последнее уравнение, то придем к исходному уравнению объекта. Таким образом, и вторая форма представления уравнений состояния эквивалентна исходному уравнению. Сами же переменные состояния в обоих случаях имеют различное определение.
3. Если дифференцирующий оператор В(р) из (1.4) имеет порядок m < n, то переход к уравнениям состояния достаточно просто осуществить по следующей схеме [7]. Положив f(t) = 0 и обозначив 
, представим
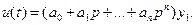
Переменные состояния
при этом
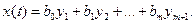
В матричных обозначениях уравнения состояния приобретают вид
.
Отметим, что переменные состояния в данном случае не содержат явного физического смысла и являются абстрактными категориями.
4. Часто свойства ОУ изменяются во времени, т.е. он нестационарен. Если объект линейный, то формально нестационарность проявляется в том, что коэффициенты в уравнении объекта изменяются во времени и являются некоторыми функциями времени. Уравнение такого объекта при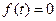 
имеет вид
. (1.15)
Причем, как и в случае стационарного объекта, 
, а часть остальных коэффициентов может обращаться в нуль. Уравнения состояния для такого объекта получают в форме подобной (1.13):
;
. (1.16)
Однако квадратная n-матрица А(t), n-мерный вектор В(t) и скаляр d(t), формирующие эти уравнения, являются функциями времени и совместно с n-мерным вектором С вычисляются в соответствии в с выражениями
; 
;
;
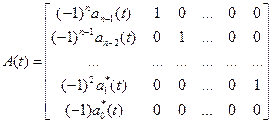. (1.17)
В свою очередь
;
. (1.18)
5. От нелинейных уравнений к уравнениям состояния переход наиболее просто осуществляется в том случае, когда нелинейное уравнение не содержит производных от управляющего воздействия и может быть разрешено относительно старшей производной выходного процесса. Пусть объект описывается уравнением
. (1.19)
которое можно разрешить относительно
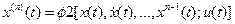. (1.20)
Обозначив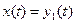 
, введем переменные состояния по правилу
... 
= 
. (1.21)
Так как в соответствии с определением 
, то из (1.20) с учетом (1.21) следует
(1.22)
Уравнения (1.21) и (1.22) совместно с уравнением для выходной координаты объекта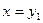 
и будут уравнениями состояния для случая (1.19). Если в рассмотрение вводится вектор-функцию Ψ (.), компонентами которой являются правые части (1.21) , (1.22), то уравнения состояния можно представить в матрично-векторной форме
(1.23)
где вектор С определен в соответствии с (1.17) .
Этот метод перехода к уравнениям состояния часто применяют и к линейным уравнениям, предварительно разрешенным относительно старшей производной. Так, для примера 1.1, обозначив известную правую часть уравнения через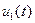 
и положив 
, в соответствии с (1.21) и (1.22) получим 
; 
или в матрично-векторной форме
; Y = 
; A = 
; B = 
6. Изложенные подходы к образованию уравнений состояния успешно можно применять и к многомерным объектам. В результате усложняются соответствующие уравнения, однако внешняя структура их сохраняется. Поэтому в последующем будем полагать, что уравнения состояния объекта в достаточно общем случае имеют вид
(1.24)
Здесь Y(t) – n-мерный вектор состояния с компонентами 
; U(t) – m-мерный вектор управлений с компонентами 
; X(t) – l-мерный вектор управляемых процессов с составляющими 
; Ψ – n-мерная вектор-функция с компонентами 
; Ф – l- мерная вектор-функция .
7. Линейные и нелинейные системы
Как мы уже говорили, все системы на самом деле нелинейные, но поскольку исследование таких систем весьма затруднительно, то принято делить системы на:
- существенно нелинейные, т.е. системы, у которых есть звенья, линеаризовать которые принципиально невозможно.
В обычном смысле слова, линеаризовать такую систему нельзя, потому что характеристика звена реле негладкая. Перейти к малым приращениям не удается.
При малом изменении входной величины существенно изменяется выход. Для таких систем существуют специальные методы исследований: так называемая теория точечных преобразований, качественная теория дифференциальных уравнений и численные методы на ЦВМ. Существенно нелинейные систем, как правило просты в реализации.
- линеаризуемые системы, т.е. системы у которых малые отклонения входных приводят к малым отклонениям выходных величин. Поэтому даже при наличии нелинейной взаимосвязи между входными и выходными величинами будем заменять нелинейную зависимость линейной.
Все линеаризованные системы записаны для определенного диапазона входных величин. Для другого участка – другие коэффициенты уравнения.
Есть система, которая явно может быть линеаризована
 |
Исходное дифференциальное уравнение нелинейное.
Дифференциальное уравнение описывает взаимосвязь на выходе и входе системы в различный момент времени. Описывает данное уравнение и то, что называется стационарным (установившимся) режимом.
Пусть есть некоторый стационарный режим с компонентами:
F (x10, O, x20,0,0)=0 ;
F (x10, O, x20,0,0)=0 - статическая характеристика системы (в дифференциальном уравнении все производные =0).
Разложим эту функцию F(…) в ряд Тейлора относительно точки х10, x20 и все производные равны 0. Удерживаем такие элементы 1-го порядка
|
- довесок
Эти производные - это для выбранной точки разложения (с индексом 0) и это числа: для входных -b, для выходных +а.
;
Уравнение линейное записано в отклонениях и линейное дифференциальное уравнение описывает поведение (уклонение) сигнала относительно его сигнала в рабочей точке (отклонения относительно х10 и х20).
Полное значение х: 
;
Если рабочая точка 
, тогда в этом случае отклонения = абсолютной величине входных и выходных величин.
Если коэффициент линеаризованного уравнения не зависит от точки разложения, то такая система является линейной.
Дата добавления: 2018-11-24; просмотров: 306; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!