Параметрическая размерность множества
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
РОССИЙСКИЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ МИРЭА
Кафедра инженерной графики
Горшков Г.Ф., Жихарев Л.А.
ПАРАМЕТРИЧЕСКИЕ МОДЕЛИРОВАНИЕ НА DELL CANVAS 27
УЧЕБНОЕ ПОСОБИЕ
По дисциплине Инженерная и компьютерная графика
МОСКВА 2018
Содержание ь
Оглавление
Введение. 3
1. Параметризация. 4
1.1. Параметрическая размерность множества. 4
1.2. Задачи параметризации. 5
1.3. Подсчет числа параметров базиса и выявление их геометрического смысла. 6
1.4. Системное представление геометрического моделирования. 6
1.5. Алгоритм создания геометрической модели. 6
2. Задания для отработки геометрических основ интерфейса. 7
Задача 1. 7
Задача 2. 7
Задача 3. 8
Задача 4. 9
3. Лабораторные работы.. 9
3.1. Лабораторная работа 1. «Параметрическое моделирование плоского обвода». 9
3.2. Лабораторная работа 2. «Трехмерное параметрическое моделирование линейных геометрических моделей». 12
3.3. Лабораторная работа 3. «Трехмерное параметрическое моделирование пространственных кривых, поверхностей и тел». 14
3.4. Лабораторная работа 4. «Трехмерное параметрическое моделирование твердотельных деталей» 18
Список литературы.. 20
Введение
В пособии приведены основы параметрической геометрии, представленной как теоретическая база параметрического моделирования и сформированной на системных принципах, заложенных в составе и структуре содержания развивающегося геометрического «ядра» САПР. Такой подход обеспечивает конструктивный доступ через интеллектуальный интерфейс к многообразию геометрических дисциплин и их широким приложениям, заложенным в базе знаний геометрического «ядра». Синтез аналитической, дифференциальной, начертательной и вычислительной геометрий, реализованный в геометрическом «ядре» САПР, отражается в интерфейсе параметрического моделирования, обеспечивая возможность их осознанного применения при решении системных задач параметрической геометрии. Развитие параметрической геометрии не только определяет направление развития параметрического моделирования, но и становиться одним из фундаментов инженерного геометрического образования.
|
|
|
При традиционности и фундаментальности трех блочной генетической структуры пособия: двухмерное пространство - плоские кривые и обводы; трехмерное пространство – линейные модели, гранные поверхности и многогранники; трехмерное пространство - криволинейные поверхности, пространственные кривые и тела, системные преставления знаний параметрической геометрии позволяют значительно увеличить число, повысить сложность и продуктивность решаемых задач, а также расширить круг предлагаемых прикладных задач, решаемых в активном диалоге со знаниями интеллектуальной системы. Так в двухмерном параметрическом моделировании доступными становятся практически все способы формообразования плоских кривых, в трехмерном параметрическом моделировании кинематические способы формообразования поверхностей и тел дополняются системой способов формообразования, значительно расширяющих прикладные возможности системы.
|
|
|
Сложно переоценить значимость параметрических моделей в современной инженерной деятельности. В условиях столь широкого применения компьютерных моделей в разработке и тестировании деталей, устройств и систем, параметрическая модель сильно упрощает поиск оптимальных инженерных решений. Простейший пример – модель детали, между параметрами толщины элементов которой установлена необходимая функциональная связь, может быть достаточно просто адоптирована под изменение условий эксплуатации с сохранением оптимальных соотношений вес-прочность. Ещё более очевидны преимущества применения параметрических моделей при создании сложных систем, которые можно подстраивать под различные элементы конструкции.
|
|
|
Пособие является частью развивающегося компьютерного комплекса, представляемого на базе одной из экспериментальных версий в виртуальной образовательной среде MOODLE на сайте dqec@mirea.ru., методические материалы которого: мультимедийные лекции, видео уроки, комплекты заданий и тестов, методические указания и т.п. доступны студенту через Internet.
Пособие предназначено для обучения основам параметрического моделирования на всех этапах построения моделей в программе Inventor с использованием современного комплекса Dell Canvas 27. Курс предполагает освоение обучающимся инновационных систем графического ввода и обработки построений, таких как стилус и шайба.
Данное пособие не содержит подробного описания алгоритма выполнения заданий в программном пакете Inventor: ввиду постоянного обновления дизайна и архитектуры программы такая информация быстро теряет актуальность. Здесь приведены лишь варианты задания и общие рекомендации касательно их выполнения. Правила работы в различных версиях программы обучающийся осваивает самостоятельно, при помощи встроенных обучающих пособий и при содействии преподавателя.
|
|
|
Параметризация
Параметрическая размерность множества
Параметрическая размерность множества - число взаимно независимых величин (параметров), позволяющих выделить элемент из заданного множества. Для множества точек пространства - это его размерность - n, для многообразий пространства (множества его подмножеств – множество линий, поверхностей, их совокупностей и т.п.) их размерность – e определяется как сумма числа независимых параметров формы – p и положения – q. От размерности пространства – n зависит число допустимых степеней свободы –Q, геометрический смысл которых в движениях поступательном и вращении относительно декартовой системы координат (Рис. 1)
Q = n (n+1) / 2
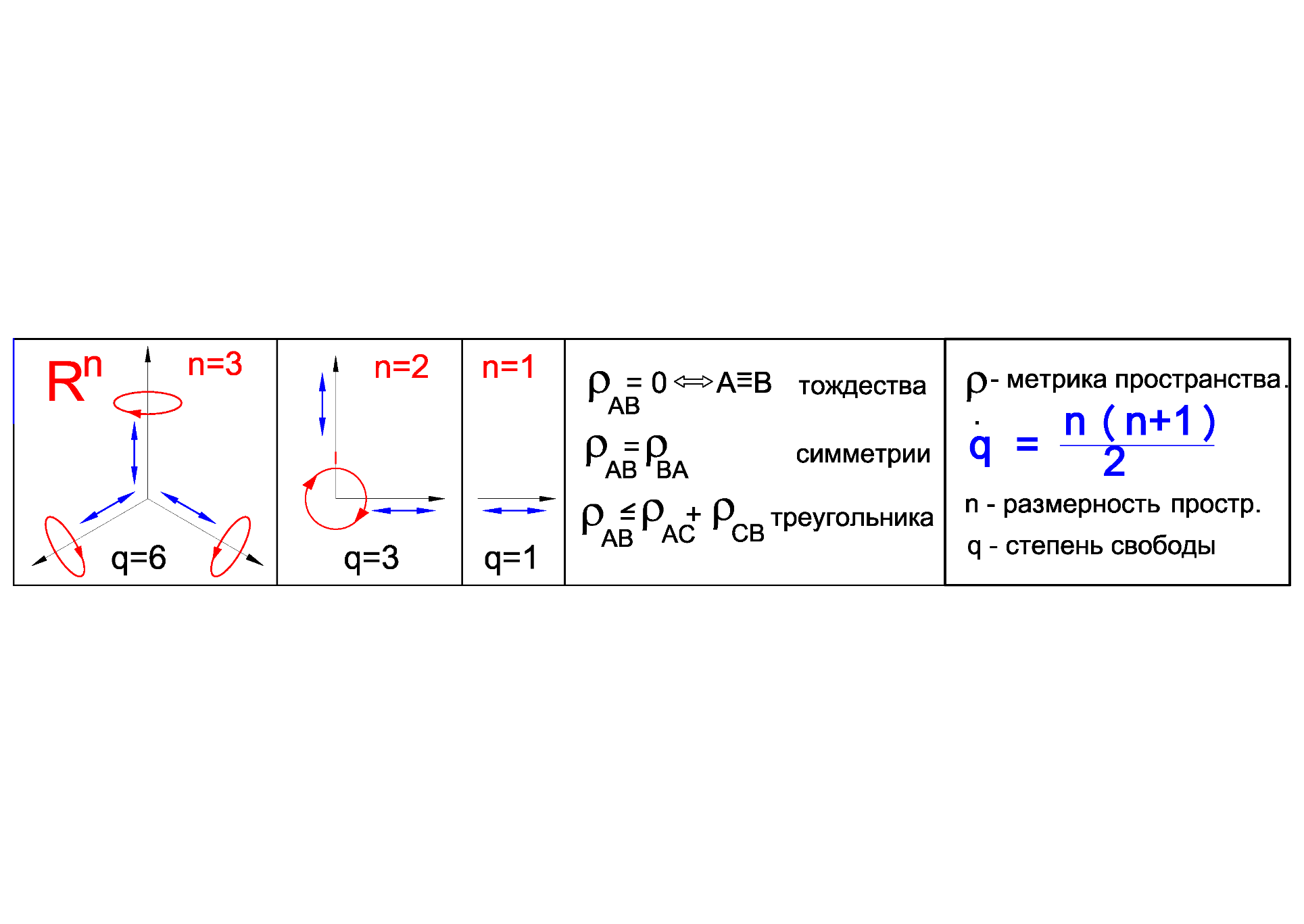
Рис. 1.
Для линейных ГФ – точки, прямой и плоскости ряд степеней свободы равны нулю, т.е. существует зависимость размерности – kq. Для точки и прямой плоскости – kq = 1, так как вращение относительно самой себя для точки и поступательное движение прямой вдоль себя не изменяют их положение. Отсюда и число параметров положения для точки и прямой на плоскости на единицу меньше допустимых степеней свободы, т.е. q = 2. В трехмерном пространстве параметрам положения точки и плоскости соответствует три параметра q = 3, так как kq = 3, а прямой четыре параметра q = 4, т.к. kq = 2.
Геометрическому смыслу параметров положения линейных ГФ соответствует геометрический смысл коэффициентов их уравнений линейных, представленных параметрами положения относительно прямоугольной декартовой системы координат (Рис. 2).
Точка А (x, y)
Прямая l (0y, j)
| 
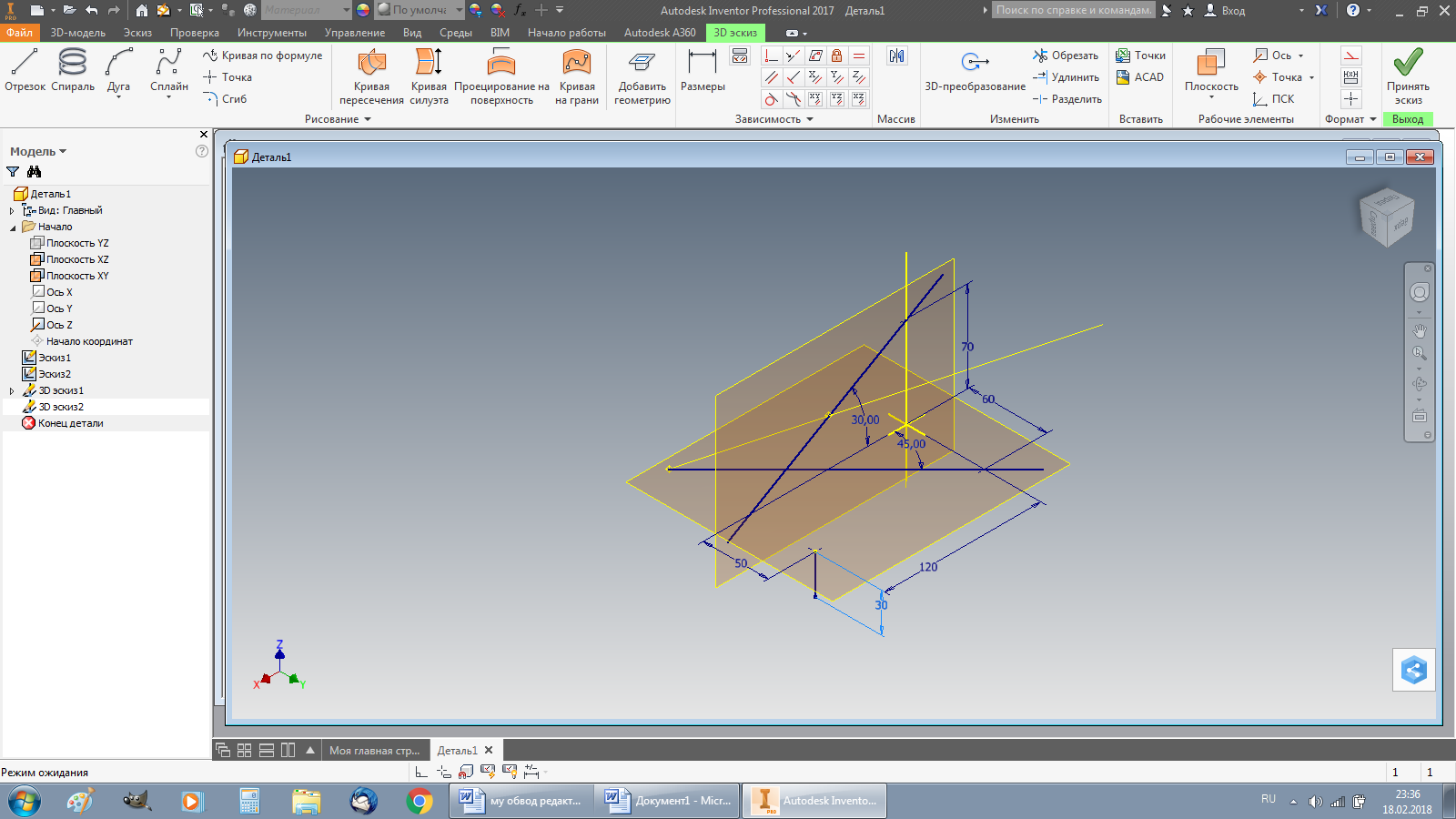Точка А (x, y, z)
Прямая l (0y, j,0z,m)
| 
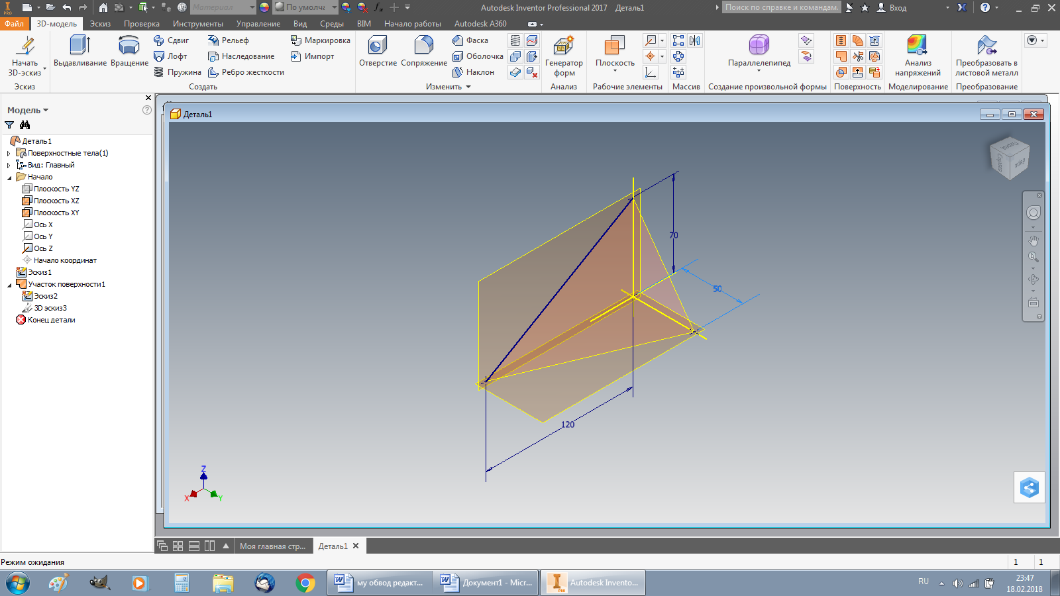Плоскость p (0x,0y,0z)
|
Рис.2.
Задачи параметризации
Если линейные ГФ не только имеют меньшее число параметров положения, но и не имею параметров формы, которые появляются с увеличением их числа в компонентах базиса. Двум линейным фигурам в сумме будет соответствовать общее число параметров больше допустимых в пространстве, что означает появление параметров формы для базиса. Так для двух точек, двух прямых, а также точки и прямой, которым на плоскости соответствует в сумме четыре параметра, одному из оставшихся от трех допустимых параметров положения будет соответствовать один параметр формы, которым будет расстояние между ними. Для выявления геометрического смысла параметров формы необходимо лишить фигуру базиса всех параметров положения, что будет соответствовать введению локальной системы координат, называемой канонической (КСК). Геометрическому смыслу параметров формы базиса будет соответствовать параметры формы элементов базиса и их параметры взаимного расположения относительно КСК.
Параметрам формы базиса будут соответствовать параметры формы, образованной на этом базисе ГФ. Однако параметры формы ГФ могут быть получены также из зависимостей, наложенных на элементы исходного множества или заданием соответствующих им параметров формы, что понижает размерность исходного множества. Параметрам формы, заложенным в условиях закона формообразования, соответствует число независимых коэффициентов системы уравнений закона.
Таким образом, в процессе порождения и развития способов порождения возникает система задач параметризации:
- подсчет числа параметров формы – p и положения – q, а также выявление их геометрического смысла;
- установление совместности (непротиворечивости) условий, заданных в зависимостях СКС;
- определение числа выделенных ГФ, соответствующих заданному закону формообразования.
Дата добавления: 2018-11-24; просмотров: 294; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!