Основные законы распределения случайной величины
В теории вероятностей известно достаточно большое количество законов распределения случайных величин. В электроэнергетике наиболее часто используются случайные величины со следующими распределениями вероятностей: равномерное, нормальное (распределение Гаусса), экспоненциальное, биноминальное, по закону Пуассона, по закону Вейбула и.т.д. В таблице 1.7. для перечисленных выше законов распределения приведены формулы для определения функций и плотности распределения распределения вероятностей, указаны основные области их применения.
è Нормальный закон распределения
Нормальным законом (законом Гаусса) называется закон распределения вероятностей непрерывной случайной величины если плотность распределения вероятностей, f(x) имеет вид:
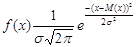(1.9)
Значения функции распределения вероятностей и плотности распределения вероятностей представлены в Приложении 2 (табл. П.2.2).
Как видно из выражения (1.9) нормальное распределение определяется только двумя параметрами: M(x) – математическим ожиданием и σ – средним квадратичным отклонением нормального распределения.
Для определения вероятности попадания нормальной случайной величины в заданный интервал, используют правило трёх сигм. Сущность этого правила заключается в следующем: если случайная величина распределена по нормальному закону, то абсолютная величина её отклонения от математического ожидания не превосходит утроенного среднего квадратичного отклонения.Другими словами, при нормальном законе распределения вероятность того, что абсолютная величина отклонения анализируемого параметра превысит утроенное среднее квадратичное отклонение σ, очень мала и не превышает 0,027. Это означает, что лишь в 0,27% всех возможных случаев так может произойти. Такие события, исходя из принципа невозможности маловероятных событий, можно считать практически невозможными.
|
|
|
Математически правило трёх сигм можно записать следующим образом:
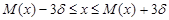(1.10)
Нормальный закон распределения имеет широкое распространение в электроэнергетике. Это объясняется тем, что именно такому закону подчиняются случайные непрерывные величины параметров режима, значения которых обусловлены действием многочисленных случайных факторов.
Пример 1.9. Построить гистограмму распределения вероятностей и по экспериментальной кривой распределения установить закон распределения. При этом имеются следующие исходные данные (табл. 1.8)
Таблица 1.8
Исходные данные
| P, МВт | p, % |
| 10-15 | 10 |
| 15-20 | 20 |
| 20-25 | 40 |
| 25-30 | 20 |
| 30-35 | 10 |
Решение
|
|
|
На основании данных таблицы 1.8. построим гистограмму распределения, вид которой свидетельствует о нормальном законе распределения анализируемой величины P и изобразим соответствующую экспериментальную кривую распределения (рис. 1.8).
|
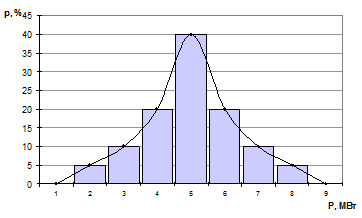
Рис. 1.8. Гистограмма и экспериментальная кривая распределения вероятностей
Пример 1.10. Определить область изменений уровней напряжения при условии нормального закона распределения. При этом имеются следующие исходные данные (табл. 1.9)
Таблица 1.9.
Исходные данные
| Параметр | Уровни напряжения | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| U,кВ | 106,5 | 108,0 | 111,5 | 110,2 | 109,4 | 112,0 | 107,9 | 109,6 |
Решение
В соответствии с выражением (1.5) – (1.7) найдём основные статистические характеристики:
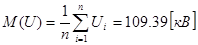
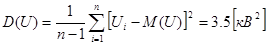
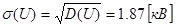
По формуле (1.10) найдём возможную область изменения уровня напряжения
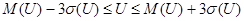
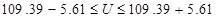
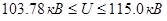
è Биноминальное распределение
Пусть проводится n независимых испытаний, в каждом из которых событие А может либо произойти, либо не произойти. Вероятность появления события A постоянна и равна p , вероятность не наступления события q =1- p
Чаще всего в качестве примера дискретной случайной величины x , рассматривается число появлений события А. Допустим, что
|
|
|
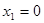- событие А не произойдёт ни разу
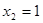- событие А не произойдёт один раз
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
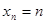- событие А не произойдёт n раз
При решении практической задачи остаётся только найти вероятности этих возможных значений, для чего используется формула Бернулли:
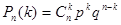(1.11)
где k=1, 2, 3,…,n
Биноминальнымназывают распределение вероятностей, определяемое формулой Бернулли, которая является аналитическим выражением искомого закона распределения. Закон назван «биноминальным» потому, что правую часть равенства (1.11) можно рассматривать как общий член разложения бинома Ньютона:
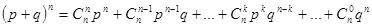
Биноминальный закон можно записать в виде таблицы 1.10.
Таблица 1.10
Биноминальное распределение
| X | n | n-1 | … | k | … | 0 |
| P |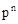 
| 
| … | 
| … | 
|
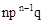
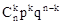
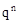
Пример 1.11. В работу вводится 2 идентичных энергоблока. Вероятность включения каждого из них равна 0,5. Записать в виде таблицы закон распределения случайной величины X .
Решение
Понятно, что энергоблоки могут либо оба включиться, либо включится один из них, либо ни один не включится. Таким образом, возможные значения X таковы: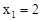 
, 
, 
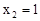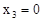. Найдём по формуле Бернулли: вероятности этих возможных значений
|
|
|
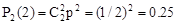
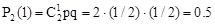
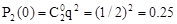
Запишем в виде таблицы искомый закон распределения:
| X | 2 | 1 | 0 |
| p | 0.25 | 0.5 | 0.25 |
Проверка: 0,25+0,5+0,25=1
è Распределение Пуассона
Распределение Пуассона (Приложение 2, табл. П.2.4) применяется в тех случаях, когда число испытаний, n велико, а вероятность возникновения события p мала (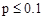 
). Кроме того, чтобы использовать формулу Пуассона необходимо принять следующее допущение 
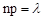. Это означает, что среднее число появлений события, k в различных сериях испытаний, т.е. при различных значениях n , остаётся неизменным.
Задача, как правило, состоит в следующем: определить вероятность того, что при большом числе испытаний n при малой вероятности p событие наступит k раз.
Закон распределения Пуассона, в упрощённой форме, выражает формула вероятностей массовых (n велико) и редких (p мало) событий:
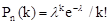(1.12)
Пример 1.12. За месяц завод произвёл 5000 вольтметров. Вероятность того, что какой-либо прибор находится вне класса точности равна 0,0002. Требуется найти вероятность того, что в указанной партии три прибора находятся вне класса точности
Решение
По условию n=5000, p=0.0002, k=3. Найдём λ:
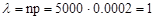
По формуле Пуассона (1.12) искомая вероятность,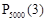 
приближённо равна:
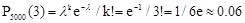
Дата добавления: 2018-11-24; просмотров: 1140; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!