Тема 1.2. Случайные величины в электроэнергетике
Лекция проводится в интерактивной форме: лекция-беседа, лекция с разбором конкретных ситуаций (2 часа).
Исторически понятие комплексного числа появилось как расширение понятия действительного числа при решении алгебраических уравнений. В общем случае среди множества действительных Как уже отмечалось, случайной называют величину, которая в результате испытания (опыта) принимает только одно возможное значение, заранее не известное и зависящее от случайных причин, которые априори не могут быть учтены.
Различают дискретные и непрерывные случайные величины. Под дискретной понимают величину, которая принимает отдельные изолированные значения с определёнными вероятностями. Например, число электроприёмников, отключенных во время аварийной ситуации. Непрерывной называют случайную величину, которая может принимать различные значения, из некоторого конечного промежутка (области) или бесконечного пространства. В качестве примера можно привести изменение величины напряжения отдельного узла электрической сети в часовом интервале времени.
Количественная оценка наиболее просто осуществляется для дискретной случайной величины. Для этой цели используются основные статистические характеристики, а именно:
· математическое ожидание, М(x);
· дисперсия, D(x);
· среднеквадратичное отклонение (электрический стандарт),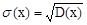 
.
Математическим ожиданием дискретной случайной величины, x называют сумму произведений всех её возможных значений,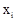 
на соответствующие вероятности их появления,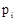 
|
|
|
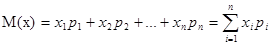(1.4)
Для дискретной случайной величины с n равновероятностными элементарными исходами выражение (1.4) можно записать в следующем виде:
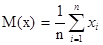(1.5)
В общем случае M(x) характеризует среднее значение анализируемой случайной величины x. К сожалению, оно не позволяет судить о степени изменчивости (разбросе) этой случайной величины. Часто необходимо знать, насколько отклоняется случайная величина от своего математического ожидания. Если эти отклонения (разбросы) невелики, что характерно для медленно изменяющихся (стабильных) случайных величин, то математическое ожидание достаточно хорошо представляет случайную величину; если же отклонения велики, т.е. разброс значений случайной величины или их рассеяния велики, то одного математического ожидания уже недостаточно для всесторонней характеристики изучаемой случайной величины. В этом случае, в качестве меры отклонений случайной величины, x от её математического ожидания M ( x ) необходимо использовать дисперсию случайной величины, D ( x ), вычисляемую как
|
|
|
(1.6)
Основные свойства математического ожидания и дисперсии дискретный случайной величины приведены в Приложении 1 (выражения П.1.12 – П.1.19)
Квадратный корень из величины дисперсии называется среднеквадратичным отклонением – электрическим стандартом,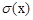 
случайной величины x
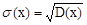(1.7)
Количественную оценку для непрерывной случайной величины осуществляют с помощью дополнительных статистических характеристик, а именно:
· интегральной функции распределения вероятностей, F(x);
· плотности распределения вероятностей, f(x)
Пример 1.6. По результатам измерений параметра тока, I в течение часа с дискретностью 10 минут (табл. 1.4) вычислить основные статистические характеристики: М(x); D(x);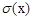 
Таблица 1.4
Данные измерений тока
| № измерения | 1 | 2 | 3 | 4 | 5 | 6 |
| I, А | 9 | 12 | 10 | 17 | 24 | 18 |
Решение.
1. В соответствии с выражением (1.5) определяем математическое ожидание, M ( I )
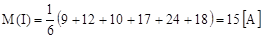
2. По формуле (1.6) произведём расчёт величины дисперсии тока, D(I)
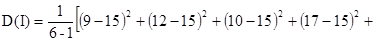
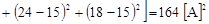
3. Используя выражение (1.7) рассчитаем величину электрического стандарта тока,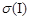 
|
|
|
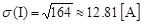
Если x – случайная величина, то вероятность того, что она примет значение, меньшее некоторого числа х, равна 
(x < х)=F(x).
Функция F ( x ) называется интегральной функцией распределения вероятностей или законом распределения вероятностей случайной величины.
Для дискретных случайных величин функция F ( x ) есть неубывающая ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям анализируемой случайной величины и равны вероятностям появления этих значений.
Пример 1.7. Длядискретной случайной величины x с известной таблицей распределения (табл. 1.5) построить функцию распределения.
Таблица 1.5.
Распределение дискретной случайной величины
| x | 1 | 4 | 8 |
| p | 0.3 | 0.1 | 0.6 |
Решение.
Согласно данным, приведённым в таблице 1.5, при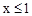 
функция распределения F ( x )=0
Если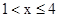 
, то F ( x )=0,3
При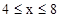 
F ( x )=0,4
Если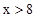 
, то F ( x )=1
В соответствии с вышеизложенным, искомая функция распределения может быть записана в виде
|
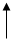
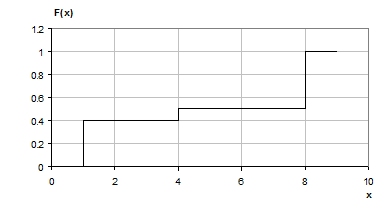
Рис. 1.5. Функция распределения дискретной случайной
величины
График этой функции представлен на рис. 1.5.
Для непрерывных случайных величин функция F(x) непрерывна для всех значений x (рис. 1.6). Как следует из рисунка график расположен в полосе, ограниченной прямыми y = 0; y = 1. При возрастании x в интервале (a, b), в котором заключены все возможные значения случайной величины, увеличивается и функция распределения от F(x)=0 до F(x)=1.
|
|
|
|
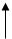
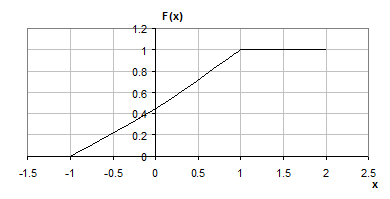
Рис. 1.6. Функция распределения непрерывной случайной величины
Знание функции распределения даёт возможность вычислить вероятности попадания непрерывной случайной величины в определённый интервал. Так, если известны значения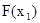 
и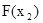 
, то искомая вероятность попадания непрерывной величины x в интервал 
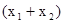окажется равной
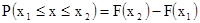
Производная от F(x) называется плотностью распределения вероятностей случайной величины, f(x).
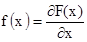(1.8)
Из выражения (1.8) следует, что определение плотности распределения вероятностей f(x) для непрерывной случайной величины возможно только при наличии F(x). В то же время необходимо подчеркнуть, что для описания функции распределения вероятности дискретной случайной величины плотность распределения вероятностей неприменима.
Таким образом, с вероятностной точки зрения, случайная величина будет полностью описана, если известен её закон распределения – соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующих им вероятностями.
При анализе непрерывных случайных величин целесообразно строить гистограмму распределения, для чего интервал, в котором заключены все значения случайной величины, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала величину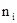 
- число измерений, попавших в i-ый интервал.
Гистограммой распределения называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которого служат частичные интервалы длиной h, а высоты равны вероятностям появления значений случайной величины в заданных интервалах.
Пример 1.8. По данным таблицы 1.6. построить гистограмму распределения параметра тока для 50 измерений
Таблица 1.6.
Исходные данные
| Число измерений частичного интервала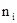
| 3 | 12 | 11 | 24 |
| Частичные интервалы длиной, h=8 А | 1-8 | 8-15 | 15-22 | 22-29 |
Решение
В соответствии с таблицей 1.6. вычислим вероятность появления тока в заданных частичных интервалах:
; 
; 
; 
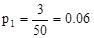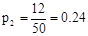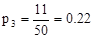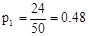
Искомая гистограмма распределения представлена на рис. 1.7.
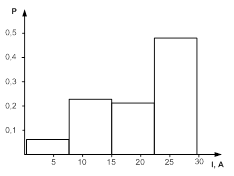
Рис.1.7. Гистограмма распределения параметра тока
Дата добавления: 2018-11-24; просмотров: 1364; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!