Графический метод представления статистических данных
Статистическим графиком называется чертеж, на котором статистические данные изображены с помощью точек, линий, геометрических фигур, а также иных символов.
Статистические распределения, представленные приведенными таблицами, можно наглядно изобразить в виде полигона, гистограммы и кумуляты. Гистограмму можно считать эмпирической плотностью вероятности, а кумуляту эмпирической функцией распределения для случайной величины (в нашем случае – веса новорожденного мальчика).
Рис.6.7. Полигон частот вариационного ряда,
представленного табл. 1 и 2.
Рис. 6.8. Гистограмма вариационного ряда,
представленного табл. 6.1 и 6.2.
Рис.6.9. Кумулята вариационного ряда, представленного табл. 2.
Напомним, что общая площадь прямоугольников, образующих гистограмму, равна 1.
Построенные графики дают основание считать распределение близким к нормальному и перейти к нахождению выборочных оценок математического ожидания и дисперсии, которые, как было сказано, полностью определяют аналитическую форму распределения.
Проверка статистических гипотез
Как указывалось, одной из задач математической статистики является проверка статистических гипотез, которые формулируются при изучении некоторой выборки 
.
Статистическая гипотеза (обозначим ее H0) — это гипотеза о предполагаемом виде изучаемого распределения вероятностей или о значениях параметров этого распределения. Например, могут проверяться гипотезы о независимости двух случайных величин, о равенстве параметров распределений и др. Используя выборку {х1, х2, …, xn} вычисляют специальную функцию (обозначим ее T) величин х1, х2, …, xn, называемую статистикой, т.е. Т = T(х1, х2, …, xn). Формулируется критерий статистической гипотезы, т.е. правило, позволяющее отвергнуть или не отвергнуть гипотезу H0 на основании выборки{х1, х2, …, xn}. Критерий определяет критическую область значений статистики T такую, что гипотеза H0 отвергается, если значение T принадлежит критической области и не отвергается в противном случае.
|
|
|
Описанное правило принятия или отбрасывания гипотезы не определяет однозначно правильность или ошибочность гипотезы. Здесь возможны четыре случая:
1) гипотеза н0 верна и принимается согласно критерию (вероятность этого обозначим α);
2) гипотеза н0 неверна и отвергается согласно критерию (вероятность этого обозначим 1-β);
3) гипотеза н0 верна, но отвергается согласно критерию (в этом случае говорят об ошибке первого рода; вероятность этого обозначим р; эта вероятность называется уровнем значимости данного критерия и равна 1-α);
4) гипотеза н0 не верна, но принимается согласно критерию (в этом случае говорят об ошибке второго рода; вероятность ее равна β).
|
|
|
Если с гипотезой н0 конкурирует лишь одна альтернативная гипотеза н1, то вероятность отвергнуть гипотезу н0, когда верна гипотеза н1 называется мощностью критерия и равна 1-β . График зависимости вероятности 1-β от вероятности р=1-α называется оперативной характеристикой критерия.
Часто поступают следующим образом: по распределению статистики т находится табличное критическое значение т0, зависящее от р – заранее заданного уровня значимости (в медико-биологических исследованиях он обычно принимается равным 0,01 или 0,05) - и проверяется неравенство т £ т0. Если равенство оказывается верным, то гипотеза н0 принимается. Если все же выяснится, что t>т0, то выдвинутая гипотеза н0 отвергается.
Пусть, например, проверяется гипотеза о том, что независимые результаты наблюдений х1 ..., хn подчиняются нормальному распределению со средним значением а= а0 при известной дисперсии s2.
Для проверки этой гипотезы находится среднее выборочное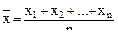 
и вычисляется статистика критерия т по формуле: т= 
.
Если бы можно было рассмотреть не единственную имеющуюся в распоряжении выборку, а все аналогичные выборки из генеральной совокупности, то статистика т была бы нормально распределенной случайной величиной т с параметрами распределения (а = 0; σ2 = 1). Задавшись уровнем значимости P (например, 0,05), по соответствующим таблицам нормального распределения можно найти критическое значение т0 (в данном случае оно равно 1,96).
|
|
|
Если т окажется больше, чем т0, то выдвинутая гипотеза о том, что выборка взята из генеральной совокупности со средним значением а0 отбрасывается.
Возвращаясь к ошибкам первого и второго рода, отметим, что для медика, обычно, более существенной является ошибка первого рода – истинно больной признан здоровым (ошибочно отвергнута гипотеза о болезни). Однако, не менее плачевной может оказаться и ошибка второго рода – признать здорового человека больным (ошибочно принятая гипотеза) и начать его лечить. Естественно требовать, чтобы критерий для проверки данной гипотезы приводил как можно реже к ошибочным решениям.
Обычная процедура построения наилучшего критерия заключается в выборе среди всех критериев с заданным уровнем значимости P (вероятность ошибочно отвергнуть) такого, который имел бы наименьшую вероятность ошибки 2-го рода b (ошибочно принять). То есть желательно иметь наибольшую вероятность отклонить ошибочную гипотезу.
|
|
|
Конечно, желательно минимизировать обе ошибки одновременно, но при заданном объеме выборки это невозможно, поскольку при уменьшении величины одной из них неизбежно будет возрастать величина другой.
Отметим, что уровень значимости – это максимально приемлемая для исследователя вероятность ошибочно отклонить гипотезу н0, когда на самом деле она верна, т.е. допускаемая исследователем величина ошибки первого рода. Величина уровня значимости устанавливается исследователем произвольно, однако обычно принимается равным 0,05 либо 0,01, либо 0,001.
Величина b-ошибки зависит от величины ожидаемого эффекта и объема выборки. Часто величина b-ошибки задается значением 0,2. С учетом допустимого уровня этого параметра существует возможность рассчитать объем выборки, необходимой для выявления эффекта определенной величины.
Дата добавления: 2018-11-24; просмотров: 242; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!