СТАТИСТИЧЕСКИЕ МЕТОДЫ ОБРАБОТКИ РЕЗУЛЬТАТОВ МЕДИКО-БИОЛОГИЧЕСКИХ ИССЛЕДОВАНИЙ
План:
1. Описание данных.
2. Законы распределения дискретных случайных величин.
3. Законы распределения непрерывных случайных величин.
4. Графический метод представления статистических данных.
5. Проверка статистических гипотез.
6. Непараметрические методы математической статистики.
Описание данных
Цель математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов. Данная цель достигается решением двух основных задач.
Первая задача математической статистики – указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов.
Вторая задача математической статистики – разработать методы анализа статистических данных в зависимости от целей исследования. Сюда относятся:
а) оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости случайной величины от одной или нескольких случайных величин и др.;
б) проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен.
Первым шагом статистического анализа является классификация типа данных, т.е. отнесение их к той или иной шкале измерений. Шкалы измерений бывают непрерывные (температура, показатель гемоглобина в крови) и дискретные (исход заболевания, группа крови). Кроме того, шкалы измерения подразделяются на:
|
|
|
· количественные (интервальные) (атмосферное давление, длительность госпитализации);
· порядковые (тестовые баллы, состояние больного);
· номинальные (цвет, пол).
Номинальная (самая «слабая») шкала. Численные значения результатов измерений служат только для обозначения отдельных возможностей, заменяя их названия и имена. Например, если значение признака может принимать значения «да» и «нет», то их можно обозначать как 1 и 0 (это, так называемая, альтернативная вариация). Здесь имеют смысл только соотношения x = y, или x ¹ y.
В порядковой шкале, например, шкала экзаменационных оценок (2, 3, 4, 5) имеют смысл только операции сравнения. Операции вроде сложения и вычитания бессмысленны.
Интервальные шкалы – это истинные количественные шкалы (длина, температура, время). Для них имеют смысл все вышеупомянутые операции и операции соотношения х ± у, ху и др.
Случайной называется величина, которая принимает в результате опыта (эксперимента) одно из множества возможных значений, причем появление того или иного значения этой величины представляет собой случайное событие. Дискретной случайной величиной называется случайная величина с конечным или счетным множеством возможных значений (например, количество детей, которые родились в роддоме за сутки). Непрерывной случайной величиной называется случайная величина, которая может принимать любое из значений, принадлежащих интервалу (интервалам), в котором она существует (например, масса тела и рост новорожденных).
|
|
|
Для задания дискретной случайной величины необходимо указать закон распределения этой величины, который может быть задан в виде таблицы, формулы или графика.
Задание функции распределения является одним из способов задания непрерывной случайной величины.
Функция распределения – это функция f(х), которая задает вероятность того, что случайная величина X в результате испытании примет значение меньше х:
F(х) = р(х<х).
Ее называют также интегральной функцией. Функция распределения непрерывной случайной величины f(х) является неубывающей непрерывной функцией.
Помимо функции распределения для задания закона распределения непрерывной случайной величины используют также функцию плотности вероятности 
, где dp – вероятность того, что случайная величина примет любое значение в интервале dx. Наряду с термином функция плотности вероятности используются термины плотность вероятности и плотность распределения. Плотность распределения является производной от функции распределения:
|
|
|
.
Закон распределения случайной величины является наиболее полной характеристикой этой случайной величины, однако, зачастую достаточно информации, которая задается с помощью числовых характеристик случайной величины, среди которых наиболее часто используются такие как: математическое ожидание, дисперсия, среднее квадратичное отклонение.
Математическое ожидание непрерывной случайной величины вычисляют по формуле: 
.
Математическое ожидание дискретной случайной величины: 
, где xi – i-е значение случайной величины х, р(хi) – вероятность i-го значения дискретной случайной величины.
Дисперсия непрерывной случайной величины может вычисляться по формуле: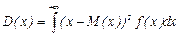 
. 
Дисперсия дискретной случайной величины может вычисляться по формуле: 
.
Среднее квадратическое отклонение 
.
Математическое ожидание м(х) близко по смыслу к понятию среднего значения случайной величины; дисперсия d(х) – это математическое ожидание квадрата отклонения случайной величины от ее математического ожидания (центра); среднее квадратичное отклонение, как и дисперсия, характеризует величину разброса значений случайной величины вокруг ее м(х).
|
|
|
Рассмотрим законы распределения, которые наиболее часто применяются при анализе медико-биологических данных.
Дата добавления: 2018-11-24; просмотров: 769; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!