Законы распределения непрерывных случайных величин

 

Нормальный закон распределения (Гаусса). В биологии и медицине чаще всего рассматривают случайные величины, которые имеют закон распределения близкий к нормальному, например, частота дыхания, частота сердечных сокращений, динамика роста популяции и др.

Для нормального закона распределения плотность вероятности задается формулой:

 

где а – математическое ожидание, а s - среднее квадратическое отклонение, s² – дисперсия.

Отметим, что стандартным нормальным распределением называют распределение с м(х) =а= 0 и d(x)= s ² = 1, плотность распределения которого имеет следующий вид:

Плотность вероятности стандартного нормального распределения имеет вид, представленный на рис.6.1, функция его распределения представлена на рис. 6.2.

 

Рис. 6.1. Плотность вероятности стандартной нормальной случайной величины

Рис.6.2. Функция распределения стандартной нормальной случайной величины

 

В случае нормального распределения изменение математического ожидания не меняет форму кривой, а только перемещает ее вдоль оси x. При изменении дисперсии форма кривой меняется (рис. 6.3). Из рисунка видно, что чем больше дисперсия, т.е. чем больше степень рассеивания случайных величин, тем более пологой и растянутой становится кривая и наоборот.

 

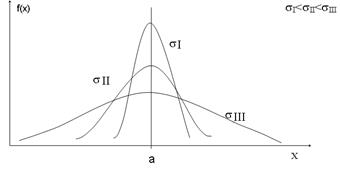
Рис. 6.3. Изменение формы плотности вероятности нормальной случайной величины в зависимости от s

 

Напомним, что площадь под графиком функции плотности вероятности равняется 1 и представляет собой вероятность достоверного события.

Рис. 6.4. График плотностинормально распределенной случайной величины с математическим ожиданием а и дисперсией s ²

 

Основное количество наблюдаемых результатов группируется вокруг наиболее вероятного значения а. В практическом применении важным является правило “трех сигм”, а именно: нормальная случайная величина с вероятностью 0,997 попадает в интервал [(а-3 s ; а+3 s)]. В интервале [(а-2 s ; а+2 s)] лежит 95,5% всех значений, а в интервале [(а- s ; а+ s)] – 68,3% всех значений.

 

Выборочное распределение и его характеристики

Пусть требуется изучить количественный признак генеральной совокупности (напомним, что генеральная совокупность – это наибольшая совокупность, объединяющая все элементы, обладающие каким-либо свойством (свойством, наличие которого позволяет причислить элементы к данной совокупности)). Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет изучаемый признак. Естественно возникает задача оценки параметров, которыми определяется это распределение. Например, если наперед известно, что изучаемый признак распределен в генеральной совокупности нормально, то необходимо оценить (приближенно найти) математическое ожидание и среднее квадратическое отклонение, так как эти два параметра полностью определяют нормальное распределение; если же есть основания считать, что признак имеет, например, распределение Пуассона, то необходимо оценить параметр а , которым это распределение определяется.

Набор значений (х₁,х₂,...,х_n) изучаемой случайной величины X, который получен в результате n опытов, называется выборкой объема n. По частоте встречаемости того или иного значения случайной величины x в выборке, можно судить о частоте встречаемости этого значения во всей генеральной совокупности. Выборка называется репрезентативной, если ее состав и структура по своим существенным характеристикам соответствуют составу и структуре генеральной совокупности.

Пусть изучаемой совокупностью являются новорожденные в большом городе за одни сутки мальчики, а признаком X является вес. Измеренные значения x_i (кг) и их частоты n_i представлены в табл. 6.1.

 

Таблица 6.1

xi	2,7	2,8	2,9	3,0	3,1	3,2	3,3	3,4	3,5	3,6	3,7	3,8	3,9	4,0	4,1	4,2	4,3	4,4
ni	1	2	3	7	8	12	13	10	7	6	5	6	6	5	3	3	2	1

 

Общее количество новорожденных

, k = 18.

В табл. 6.1 измеренные значения признака (варианты) представлены в возрастающем порядке, во второй строке приведены соответствующие числа наблюдений n_i каждой варианты (частоты). Таблица 1 представляет собой статистическое распределение веса новорожденных в рассматриваемой совокупности, которое называют также вариационным рядом.

Полученное распределение может быть представлено в виде интервального вариационного ряда (табл. 6.2) путем преобразования дискретной случайной величины в непрерывную.

Для построения табл. 6.2 всю область возможных весов новорожденных мы разбили на 18 одинаковых интервалов или классов с одинаковой шириной Δх=0,1. Поскольку непрерывная случайная величина характеризуется плотностью вероятности и функцией распределения, выборочными оценками которых являются плотность относительной частоты и кумулятивная относительная частота соответственно. Табл. 2 дополнена строками, содержащими значения этих величин.

 

Таблица 6.2

Номер класса	1	2	…	8	…	17	18
Классовый интервал	[2,65;2,75[	[2,75;2,85[	…	[3,35;3,45[	…	[4,25;4,35[	[4,35;4,45]
Частота (ni)	1	2	…	10	…	2	1
Относительная частота	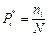	0,02	…		…	0,02	0,01
Плотность относительной частоты			…		…	0,2	0,1
Кумулятивная относительная частота	0,01	0,03	…	0,01+0,02+…+0,13+0,1=0,56	…	0,99	1,0

 

Точечной оценкой математического ожидания  является среднее выборочное значение, вычисляемое по формуле: . Подставляя значения из табл.6.1, получим:

(2,7∙1+2,8∙2+…+4,3∙2+4,4∙1)=3,383

Точечной оценкой дисперсии является выборочная дисперсия s², вычисляемая по формуле : .

Для нашего примера s²=0,1580 кг².

---

Дата добавления: 2018-11-24; просмотров: 189; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!