Законы распределения дискретных случайных величин
Биномиальное распределение (распределение Бернулли).Биномиальное распределение – это распределение числа появлений некоторого события (обозначим его а) в серии из n независимых испытаний, причем, в каждом из этих испытаний вероятность события постоянна (обозначим ее р). Таким образом, рассматриваемая дискретная случайная величина (X) может принимать одно из следующего ряда значений 0,1,2,…m…,n, где m – произвольное значение величины X. Вероятность появления значения m вычисляется по формуле Бернулли:
где q=1-p, 
.
Числовые характеристики случайной величины X, распределенной по биномиальному закону вычисляется по формулам:
M(X) = np, d(X) = npq
Еще раз подчеркнем, что здесь исходом каждого испытания могут быть только два противоположных события (а и`а, да – нет, верно – неверно, орел – решка, положительный исход лабораторного эксперимента – отрицательный исход и т.д.). Эти совокупности, состоящие из элементов только двух типов, называемые двузначными или дихотомическими, часто встречаются на практике.
Пример. Пусть х – число рецессивов среди n потомков полученных при скрещивании двух гибридов gg´gg. По теории Менделя вероятность того, что потомок двух гибридов будет рецессивом, равняется 0,25. В рамках теории Менделя X является случайной биномиально распределенной величиной с вероятностью:
.
То есть, подставляя определенные значения, m получим вероятность появления m рецессивов среди n потомков.
|
|
|
Распределение Пуассона. Это распределение встречается во многих практических задачах (например, при анализе заболеваемости, посещаемости лечебно-профилактических учреждений, вызовов скорой помощи, требований на выплату страховых сумм за год и т.д.). Рассмотрим дискретную величину X, которая может принимать целые неотрицательные значения 0,1,2,…,m... Считается, что последовательность значений не ограничена. Говорят, что случайная величина Х распределена по закону Пуассона, если вероятность того, что она примет определенное значение - m, равна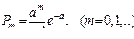 
, где а – параметр закона Пуассона, а>0. Математическое ожидание и дисперсия равны между собой и равны параметру распределения: м(X)=d(X)=а. Закон Пуассона является предельным для биномиального распределения, если одновременно n ® ¥, а р ® 0, причем nр сохраняется постоянным и равно параметру распределения: nр = а. Обычно формулу Пуассона используют при а < 4 и р < 0,1. Из-за свойства закона Пуассона отражать биномиальное распределение при большом числе опытов и малой вероятности события он имеет еще другое название – закон редких событий.
Распределение Пуассона встречается в задачах с последовательностью случайных событий, т.е. с событиями, наступающими один за другим в случайные моменты времени. При этом должны выполняться условия:
|
|
|
1) вероятность появления любого числа событий за некоторый промежуток времени зависит от длительности промежутка и не зависит от начала отсчета и от того, сколько раз это событие уже произошло.
2) за малый промежуток времени вероятность наступления одного события пропорциональна длительности этого промежутка и значительно превышает вероятность появления двух или более событий.
Пример. Вакцина формирует иммунитет к некоторому заболеванию с вероятностью 0,999. Вакцинировано 4000 жителей города. Какова вероятность того, что двое из них не приобрели иммунитет.
а=np=4000 ´ 0,001=4
Дата добавления: 2018-11-24; просмотров: 243; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!