Преобразования симметрии абсолютных тензоров четвертого, второго и первого рангов
Введем в рассмотрение абсолютные тензоры [19]: 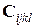 – тензор четвертого ранга;
– тензор четвертого ранга;  – тензор второго ранга; V i – тензор первого ранга (вектор), причем тензоры
– тензор второго ранга; V i – тензор первого ранга (вектор), причем тензоры 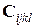 и
и  удовлетворяют следующим условиям симметрии:
удовлетворяют следующим условиям симметрии: 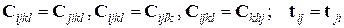 ; следовательно, тензор
; следовательно, тензор 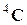 содержит 21 независимый компонент; тензор t содержит 6 независимых компонентов;вектор V содержит 3 независимых компонента.
содержит 21 независимый компонент; тензор t содержит 6 независимых компонентов;вектор V содержит 3 независимых компонента.
Пусть 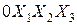 – исходная прямолинейная ортогональная система координат, a
– исходная прямолинейная ортогональная система координат, a  – новая система координат, получающаяся из исходной преобразованиями симметрии (2.2.1);
– новая система координат, получающаяся из исходной преобразованиями симметрии (2.2.1); 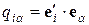 – косинус угла между осями
– косинус угла между осями 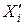 и
и 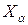 ;
; 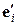 ,
,  – единичные векторы, задающие направления новой оси
– единичные векторы, задающие направления новой оси 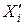 и старой оси. При переходе от исходной системы координат к новой системе координат при помощи преобразования симметрии компоненты тензоров
и старой оси. При переходе от исходной системы координат к новой системе координат при помощи преобразования симметрии компоненты тензоров  и V преобразуются по следующим правилам:
и V преобразуются по следующим правилам:
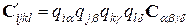

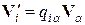
Результаты применения восьми преобразований симметрии (2.1.2) к тензорам  , V содержатся в таблицах 2.1, 2.2, 2.3.
, V содержатся в таблицах 2.1, 2.2, 2.3.
Первые столбцы этих таблиц содержат компоненты тензоров в исходной системе координат, что является результатом применения операции тождественности.
Таблица 2.1
Таблица инвариантности
(преобразования симметрии абсолютного тензора четвертого ранга  )
)
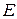
| 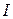
| 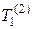
| 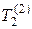
| 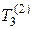
| 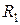
| 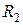
| 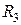
|
| C 1111 | C 1111 | C 1111 | C 1111 | C 1111 | C 1111 | C 1111 | C 1111 |
| C 1122 | C 1122 | C 1122 | C 1122 | C 1122 | C 1122 | C 1122 | C 1122 |
| C 1133 | C 1133 | C 1133 | C 1133 | C 1133 | C 1133 | C 1133 | C 1133 |
| C 1123 | C 1123 | C 1123 | – C 1123 | – C 1123 | C 1123 | – C 1123 | – C 1123 |
| C 1131 | C 1131 | – C 1131 | C 1131 | – C 1131 | – C 1131 | C 1131 | – C 1131 |
| C 1112 | C 1112 | – C 1112 | – C 1112 | C 1112 | – C 1112 | – C 1112 | C 1112 |
| C 2222 | C 2222 | C 2222 | C 2222 | C 2222 | C 2222 | C 2222 | C 2222 |
| C 2233 | C 2233 | C 2233 | C 2233 | C 2233 | C 2233 | C 2233 | C 2233 |
| C 2223 | C 2223 | C 2223 | – C 2223 | –C 2223 | C 2223 | – C 2223 | – C 2223 |
| C 2231 | C 2231 | – C 2231 | C 2231 | – C 2231 | – C 2231 | C 2231 | – C 2231 |
| C 2212 | C 2212 | – C 2212 | – C 2212 | C 2212 | – C 2212 | – C 2212 | C 2212 |
| C 3333 | C 3333 | C 3333 | C 3333 | C 3333 | C 3333 | C 3333 | C 3333 |
| C 3323 | C 3323 | C 3323 | – C 3323 | – C 3323 | C 3323 | – C 3323 | – C 3323 |
| C 3331 | C 3331 | – C 3331 | C 3331 | – C 3331 | – C 3331 | C 3331 | – C 3331 |
| C 3312 | C 3312 | – C 3312 | – C 3312 | C 3312 | – C 3312 | – C 3312 | C 3312 |
| C 2323 | C 2323 | C 2323 | C 2323 | C 2323 | C 2323 | C 2323 | C 2323 |
| C 2331 | C 2331 | – C 2331 | – C 2331 | C 2331 | – C 2331 | – C 2331 | C 2331 |
| C 2312 | C 2312 | – C 2312 | C 2312 | – C 2312 | – C 2312 | C 2312 | – C 2312 |
| C 3131 | C 3131 | C 3131 | C 3131 | C 3131 | C 3131 | C 3131 | C 3131 |
| C 3112 | C 3112 | C 3112 | – C 3112 | – C 3112 | C 3112 | – C 3112 | – C 3112 |
| C 1212 | C 1212 | C 1212 | C 1212 | C 1212 | C 1212 | C 1212 | C 1212 |
Приведенные таблицы уместно назвать таблицами инвариантности, ибо в них содержится информация об инвариантности или неинвариантности (смене знака) компонентов тензоров  , V относительно преобразований симметрии (2.1.2).
, V относительно преобразований симметрии (2.1.2).
|
|
|
Таблица 2.2
Таблица инвариантности
(преобразования симметрии абсолютного тензора второго ранга t)
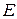
| 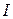
| 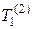
| 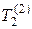
| 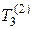
| 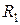
| 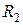
| 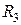
|
| t 11 | t 11 | t 11 | t 11 | t 11 | t 11 | t 11 | t 11 |
| t 22 | t 22 | t 22 | t 22 | t 22 | t 22 | t 22 | t 22 |
| t 33 | t 33 | t 33 | t 33 | t 33 | t 33 | t 33 | t 33 |
| t 12 | t 12 | – t 12 | – t 12 | t 12 | – t 12 | – t 12 | t 12 |
| t 23 | t 23 | t 23 | – t 23 | – t 23 | t 23 | – t 23 | – t 23 |
| t 31 | t 31 | – t 31 | t 31 | – t 31 | – t 31 | t 31 | – t 31 |
Таблица 2.3
|
|
|
Таблица инвариантности
(преобразования симметрии абсолютного тензора первого ранга V)
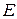
| 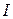
| 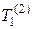
| 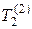
| 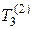
| 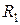
| 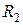
| 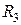
|
| V 1 | – V 1 | V 1 | – V 1 | – V 1 | – V 1 | V 1 | V 1 |
| V 2 | – V 2 | – V 2 | V 2 | – V 2 | V 2 | – V 2 | V 2 |
| V 3 | – V 3 | – V 3 | – V 3 | V 3 | V 3 | V 3 | – V 3 |
2.3. Анизотропные тела и макроскопически анизотропные среды
(принцип Неймана)
Для кристаллов связь между симметрией структуры и симметрией физических свойств устанавливается принципом Ф. Неймана (основной закон кристаллофизики) [20–23]:
“ Элементы симметрии любого физического свойства кристалла должны включать элементы симметрии точечной группы кристалла ”.
Из принципа Неймана следует, что физические свойства (в том числе упругие свойства) инвариантны относительно преобразований: симметрии, свойственных кристаллу – всякое преобразование симметрии кристалла является преобразованием симметрии и для его физических свойств. Важно отметить, что принцип Неймана распространяется и на тела, не являющиеся кристаллами, но обладающие симметрией структуры – микронеоднородные тела [3].
Характерными особенностями кристаллов являются однородность, анизотропия и симметрия физических свойств, обусловленные симметрией их внутреннего строения. В случае микронеоднородных тел будем говорить о макроскопической гомогенности, макроскопической анизотропии и симметрии макроскопических (эффективных) физических свойств, обусловленных симметрией структуры микронеоднородных тел.
|
|
|
Анизотропные тела (кристаллы) и макроскопические анизотропные среды в зависимости от их структуры делятся на три категории (низшую, среднюю, высшую), семь систем (сингоний): триклинную, моноклинную, ромбическую, тригональную, тетрагональную, гексагональную, кубическую и 32 класса симметрии. Введенные ранее преобразования симметрии (2.1.2) позволяют полностью характеризовать только низшую категорию: триклинную, моноклинную и ромбическую системы.
Триклинная система (2 класса). Характерными преобразованиями симметрии являются тождественное преобразование и преобразование инверсии. Из таблицы инвариантности 2.1 следует, что тензор модулей упругости  (тензор упругих податливостей
(тензор упругих податливостей 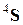 ) и тензор эффективных модулей упругости
) и тензор эффективных модулей упругости 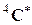 (тензор эффективных упругих податливостей
(тензор эффективных упругих податливостей 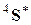 ) содержат по 21 независимому компоненту (если следовать Л.Д. Ландау и Е.М. Лифшицу [24], тогда 21 независимым компонентом, характеризующим упругие свойства, будут 18 отличных от нуля модулей и 3 угла, определяющих ориентацию осей в кристалле или микронеоднородном теле).
) содержат по 21 независимому компоненту (если следовать Л.Д. Ландау и Е.М. Лифшицу [24], тогда 21 независимым компонентом, характеризующим упругие свойства, будут 18 отличных от нуля модулей и 3 угла, определяющих ориентацию осей в кристалле или микронеоднородном теле).
|
|
|
Моноклинная система (3 класса). Характерным преобразованием симметрии является любое из вращений 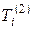 или любое из отражений Ri. Из таблицы инвариантности 2.1 следует, что тензоры модулей упругости
или любое из отражений Ri. Из таблицы инвариантности 2.1 следует, что тензоры модулей упругости 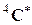 и
и 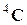 содержат по 13 независимых компонентов (по Ландау и Лифшицу – 12 отличных от нуля модулей и один угол, определяющий ориентацию осей, перпендикулярных оси вращения Хi или осей в плоскости отражения
содержат по 13 независимых компонентов (по Ландау и Лифшицу – 12 отличных от нуля модулей и один угол, определяющий ориентацию осей, перпендикулярных оси вращения Хi или осей в плоскости отражения 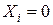 ).
).
Ромбическая система (3 класса). Характерными преобразованиями симметрии являются любые два вращения 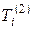 или любые два отражения Ri. Из таблицы инвариантности 2.1 следует, что выбором любых двух вращений
или любые два отражения Ri. Из таблицы инвариантности 2.1 следует, что выбором любых двух вращений 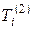 или любых двух отражений Ri число модулей упругости уменьшается до 9. Добавление третьего вращения или третьего отражения уже не приводит к дальнейшему сокращению числа независимых компонентов тензоров
или любых двух отражений Ri число модулей упругости уменьшается до 9. Добавление третьего вращения или третьего отражения уже не приводит к дальнейшему сокращению числа независимых компонентов тензоров 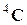 и
и 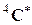 . Группа симметрии с элементами (2.1.2) характеризует ромбически-дипирамидальный класс (название класса дано по Гроту); такое же название принято и в литературе по механике сплошных сред [25, 26].
. Группа симметрии с элементами (2.1.2) характеризует ромбически-дипирамидальный класс (название класса дано по Гроту); такое же название принято и в литературе по механике сплошных сред [25, 26].
Тело, обладающее тремя ортогональными плоскостями упругой симметрии в каждой точке, называется ортотропным. Уравнения обобщенного закона Гука для ортотропного тела имеют вид (1.1.7).
К средней категории относятся тригональная, тетрагональная и гексагональная системы.
Тригональная система (5 классов). Преобразованием симметрии, характеризующим данную систему, является вращение 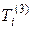 . Число независимых упругих модулей – 7 или 6, в зависимости от принадлежности к тому или иному классу.
. Число независимых упругих модулей – 7 или 6, в зависимости от принадлежности к тому или иному классу.
Тетрагональная система (7 классов). Характерным преобразованием симметрии является вращение 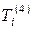 . Число независимых упругих модулей – 7 или 6, в зависимости от класса.
. Число независимых упругих модулей – 7 или 6, в зависимости от класса.
Гексагональная система (7 классов). Преобразованием симметрии, характеризующим данную систему, являются вращение 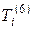 . Число независимых упругих модулей – 5 во всех классах симметрии.
. Число независимых упругих модулей – 5 во всех классах симметрии.
Рассмотрим тело, упругие свойства которого инвариантны относительно преобразования 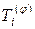 – вращение вокруг оси Хi на угол j. Такое тело называется трансверсально-изотропным [16,3]. Тензор модулей упругости
– вращение вокруг оси Хi на угол j. Такое тело называется трансверсально-изотропным [16,3]. Тензор модулей упругости  трансверсально-изотропного тела и тензор эффективных модулей упругости
трансверсально-изотропного тела и тензор эффективных модулей упругости 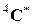 макроскопически трансверсально-изотропной гетерогенной среды содержат по 5 независимых упругих модулей.
макроскопически трансверсально-изотропной гетерогенной среды содержат по 5 независимых упругих модулей.
Кубическая система (5 классов). Данная система принадлежит к высшей категории; характерными преобразованиями симметрии являются четыре вращения 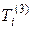 . Тензоры модулей упругости
. Тензоры модулей упругости 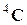 и
и 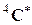 содержат по 3 независимых компонента.
содержат по 3 независимых компонента.
Рассмотрим тело, упругие свойства которого инвариантны относительно двух преобразований – 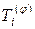 ,
, 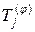 (оси Хi и Хj взаимно ортогональные оси). Инвариантность относительно третьего вращения
(оси Хi и Хj взаимно ортогональные оси). Инвариантность относительно третьего вращения  не приводит к дальнейшему уменьшению числа упругих модулей (0 Хi Хj Хk – ортогональная система координат). В рассматриваемом теле упругие свойства одинаковы во всех направлениях. Тензоры модулей упругости
не приводит к дальнейшему уменьшению числа упругих модулей (0 Хi Хj Хk – ортогональная система координат). В рассматриваемом теле упругие свойства одинаковы во всех направлениях. Тензоры модулей упругости  и
и 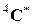 содержат по 2 независимых компонента.
содержат по 2 независимых компонента.
Дата добавления: 2015-12-17; просмотров: 22; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
