Некоторые сведения из механики композиционных материалов
1.1. Основные соотношения теории упругости
гетерогенной анизотропной среды [1, 2, 3]
1.1.1. Дифференциальные уравнения равновесия. Граничные условия. Квазистатическая задача теории упругости в перемещениях для гетерогенной анизотропной среды заключается в решении трех дифференциальных уравнений равновесия относительно компонентов вектора перемещения:
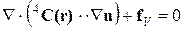, (1.1.1)
где r – вектор-радиус рассматриваемой точки; u – вектор перемещения; Ñ – набла-оператор Гамильтона;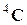 
– тензор модулей упругости, тензор 4-го ранга; 
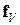– вектор объемныхсил; символ “٠” обозначает операцию свертки.
К системе уравнений (1.1.1), определяющих поведение тела в точках его объема V, добавляются условия на ограничивающей его поверхности S – кинематические, статические или смешанные граничные условия:
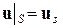(1.1.2)
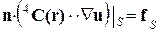(1.1.3)
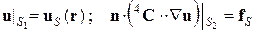, (1.1.4)
где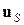 
– заданный на границе вектор перемещения; 
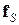– заданная на границе поверхностная нагрузка; n – единичный вектор внешней нормали к поверхности тела; в случае (1.1.4) поверхность S состоит из двух частей S 1, S 2.
Возможны также и комбинированные граничные условия, когда из трех равенств, которые должны быть заданы в каждой точке поверхности S,одно (два) формулируется в перемещениях, а два (одно) – в силах. Граничные условия такого рода будем называть кинематико-статическими.
1.1.2. Определяющие соотношения. В случае малых деформаций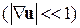 
тензор деформации e выражается через вектор перемещения u соотношениями Коши:
|
|
|
(1.1.5)
где (¼)T – операция транспонирования; (¼)S – операция симметрирования.
Определяющие соотношения для линейной гетерогенной анизотропной упругой среды записываются в следующем виде (обобщенный закон Гука):
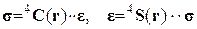, (1.1.6)
где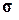 
– тензор напряжений, 
; 
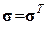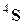– тензор упругих податливостей, тензор 4-го ранга, причем тензоры 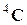и 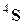взаимообратны.
Для композиционных материалов тензор упругих модулей 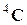и тензор упругих податливостей 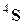являются разрывными функциями координат. Для i -ой фазы композита в случае анизотропии общего вида тензор 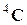(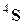) содержит 21 независимый компонент, для ортотропного тела тензор 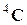(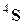) имеет 9 независимых компонентов, для трансверсально-изотропного тела – 5, для изотропного тела – 2 независимых компонента (например, постоянные Ламе).
В прямолинейной ортогональной системе координат 0Х1X2X3 рассмотрим ортотропное тело. Уравнения обобщенного закона Гука запишем в следующей форме:
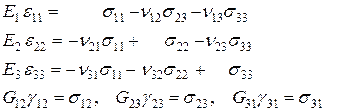(1.1.7)
В уравнениях (1.1.7) введены в рассмотрение “технические константы” упругости: Е 1, E 2, Е 3 – модулиЮнга при растяжении-сжатии в направлении ортогональных осей 1,2,3; G 12, G 23, G 31 – модули сдвига дня плоскостей, параллельных координатным; 
– коэффициенты Пуассона, характеризующие сокращение в направлении одной оси при растяжении в направлении другой (например,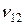 
– коэффициент, характеризующий сокращение в направлении оси 2 при растяжении в направлении оси 1). МодулиЮнга и коэффициенты Пуассона связаны равенствами:
|
|
|
(1.1.8)
Определяющие соотношения можно записать и так:
(1.1.9)
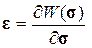(1.1.10)
В несвязанных квазистатических задачах термоупругости определяющие соотношения имеют вид:
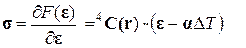(1.1.11)
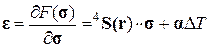(1.1.12)
, (1.1.13)
где F – термодинамическая функция состояния, называемая свободной энергией; a – тензор коэффициентов линейного температурного расширения, тензор 2-го ранга;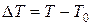 
– перепад температуры; T 0, T – температура недеформированного и деформированного состояния.
Определяющие соотношения (1.1.11) называются соотношениями Дюамеля – Неймана.
1.2. Некоторые определения и исходные предпосылки.
Представительный элемент объема [4–14]
1.2.1. Определения и исходные предпосылки. Композиционными материалами (композитами) называются материалы, состоящие из двух или нескольких компонентов (фаз) с отчетливо выраженными поверхностями сопряжения и различными физико-механическими свойствами. Ради удобства одну из фаз будем называть матрицей и обозначать m (matrix); а другие фазы – включениями и обозначать f 1, f 2, ¼, (filament).Последний термин будет относиться к любой фазе, заключенной в матрице; таким образом, этот термин охватывает и пустоты, каналы.
|
|
|
Композиционные материалы обычно классифицируются по форме включений. Композит, включения которого представляют собой длинные цилиндры, называется волокнистым композитом. Если же эти цилиндры (волокна) параллельны между собой, то волокнистый композит называется однонаправленным. При изучении механического поведения волокнистых упругих композитов обычно делаются следующие предположения:
1. Матрица и включения – линейно-упругие, однородные, изотропные: связь между напряжениями и деформациями в компонентах композита описывается законом Гука;
2. Отдельные компоненты композита идеально связаны между собой – на поверхностях сопряжения компонентов реализуются условия непрерывности векторов перемещения и напряжений:
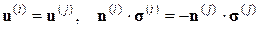, (1.2.1)
где n – единичный вектор внешней нормали к поверхности компонента; индексом (i) помечены величины, относящиеся к одной фазе, а индексом ( j ) – к другой;
3. Волокнистый композит представляет собой линейно-упругий макроскопически однородный материал без начальных напряжений; в зависимости от укладки волокон материал принимается трансверсально-изотропным или ортотропным.
|
|
|
Если геометрические характеристики (форма, размеры, расположение) и физико-механические свойства компонентов периодически повторяются в пространстве – композит называется композитом с периодической структурой:
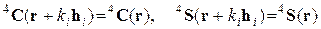, (1.2.2)
где ki – произвольные целые числа; h i – постоянные векторы, определяющие период структуры.
Если в соотношениях (1.2.2) i принимает значения 1 и 2 (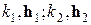
), то среда называется средой с двоякопериодической структурой. Точки P 1 и P 2, вектор-радиусы которых связаны соотношением
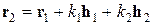(1.2.3)
называются конгруэнтными. На плоскости 0X1X2 выделим область, не содержащую двух конгруэнтных точек, такую, что для любой внешней точки внутри области найдется ей конгруэнтная точка. В общем случае эта область является параллелограммом и называется параллелограммом периодов; употребляется также термин ячейка периодичности. Пара целых чисел (k 1, k 2) является идентификатором ячейки периодичности.
Взаимодействие выделенной ячейки периодичности с окружающей средой учитывается точно, если выполняются условия двоякой периодичности тензора напряжений s и квазипериодичности вектора перемещения u:
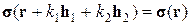(1.2.4)
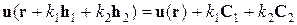, (1.2.5)
где C 1 и C 2 – постоянные векторы. В дальнейшем, не ограничивая общности, считаем, что векторы h i и C i имеют вид:
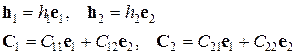(1.2.6)
1.2.2. Представительный элемент объема гетерогенной среды. Задачи микромеханики и макромеханики, возникающие при изучении механического поведения композиционных материалов, различаются уровнем описания неоднородностей. В задачах микромеханики в качестве характерного масштаба длины l выступает характерный размер неоднородности: расстояние между включениями, диаметр включения и т.п. В задачах макромеханики характерным масштабом длины L является расстояние, на котором макроскопические напряжения изменяются значительно; обычно, это характерный размер конструкции. Ясно, что существует некоторый промежуточный масштаб длины l, в пределах которого является осмысленной операция гомогенизации: замена гетерогенной среды эквивалентной ей в некотором смысле гомогенной средой.
Введем в рассмотрение элемент объема гетерогенной среды, имеющий характерный размер l и обладающий геометрическими и физико-механическими свойствами рассматриваемой среды. Этот элемент объема называется представительным элементом объема.
Из практических соображений очень важно, чтобы представительный элемент объема имел минимально допустимые размеры. Весьма благоприятна ситуация, когда гетерогенная среда имеет периодическую структуру – в этом случае
- можно точно учесть взаимодействие выделенного элемента объема с окружающим пространством, если выделить всего лишь одну ячейку периодичности;
- все средние по объему ячейки периодичности тензоры деформаций и напряжений равны соответствующим средним тензорам, вычисленным для гетерогенной среды в целом.
Итак, представительный элемент объема – это элемент объема, который обладает геометрическими и физико-механическими свойствами рассматриваемой гетерогенной среды и в котором средние по объему тензоры деформаций и напряжений равны соответствующим средним тензорам, вычисленным для гетерогенной среды в целом.
Несколько слов о терминологии. Термин микроскопический (микродеформации, микронапряжения) употребляется по отношению к областям меньше представительного элемента объема, т.е. имеющим характерный масштаб длины l. Термин макроскопический (макроскопические свойства, деформации и напряжения) относится к областям, большим представительного элемента объема; при этом предполагается, что макроскопические напряжения изменяются достаточно медленно от точки к точке, так что в представительном элементе объема их можно считать постоянными.
Определим процедуру осреднения по объему представительного элемента:
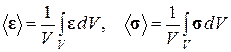, (1.2.7)
где V – объем представительного элемента; 
– средний тензор микродеформаций (макроскопический тензор деформаций);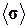 
– средний тензор микронапряжений (макроскопический тензор напряжений).
В i -м компоненте представительного элемента объема напряжения и деформации связаны обобщенным законом Гука. Осреднив по объему V ( i ) соотношение (1.1.6), установим связь между средними тензорами микронапряжений и микродеформаций для i- го компонента:
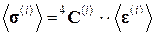(1.2.8)
Нас же будет интересовать связь между макроскопическими тензорами напряжений и деформаций для всего представительного элемента объема.
Дата добавления: 2015-12-17; просмотров: 29; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!