Преобразования симметрии. Группы симметрии
2.1.1. Преобразования симметрии. Преобразования пространственного объекта, приводящие объект в новое положение, которое в точности совпадает с начальным положением и от него физически не отличается, называются преобразованиями (операциями) симметрии; расстояния между всеми парами точек пространственного объекта остаются неизменными, т.е. объект не испытывает растяжения, сжатия, изгиба.
Введем в рассмотрение следующие операции симметрии:
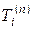– вращение вокруг оси Xi на угол 2p/ n против часовой стрелки; ось вращения Xi называется осью симметрии n -го порядка;
Ri – отражение от плоскости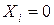 
, которая называется плоскостью симметрии;
E – тождественность (операцию тождественности можно рассматривать как вращение на угол2p);
I – инверсия (операция инверсии представляет собой особый случаи вращения вокруг оси Xi на угол p с последующим отражением от плоскости 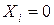; точка 
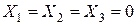называется центром инверсии или центром симметрии).
Преобразования симметрии можно описать аналитически как ортогональные преобразования координат:
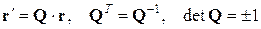, (2.1.1)
где r – вектор-радиус рассматриваемой точки; r¢ – вектор-радиус рассматриваемой точки после преобразования симметрии; Q – ортогональный тензор.
Преобразования симметрии осуществляются при помощи элементов симметрии. Элементы симметрии состоят из группы точек, которые не перемещаются при операциях симметрии – плоскости симметрии, оси симметрии, центр симметрии.
Преобразования симметрии 
представляют собой точечные преобразования симметрии, так как при этих преобразованиях пространственный объект не перемещается как целое и хотя бы одна его точка остается на месте.
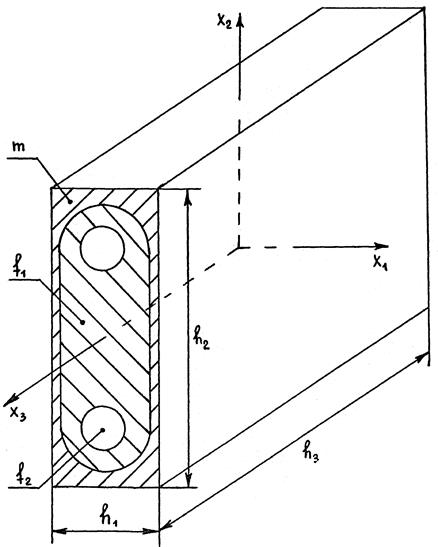
2.1.2. Группы симметрии. Рассмотрим представительный элемент объема гетерогенной среды (рис. 2.1).
|
Рис. 2.1. Представительный элемент объема (ячейка периодичности)
Начало прямолинейной ортогональной системы координат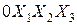 
расположим в точке, которая остается неподвижной при всех преобразованиях симметрии. Выпишем преобразования симметрии, которые оставляют инвариантным представительный элемент объема:
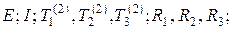(2.1.2)
Составим таблицу умножения Кэли, в которой представлены все возможные произведения элементов (2.1.2), записанные в следующем виде: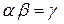 
(a и b взяты из первого столбца и первой строки таблицы, а g находится на пересечении соответствующих строки и столбца).
Исследованием таблицы Кэли можно установить [17, 18], что множество элементов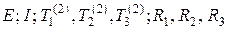 
образует группу G, так как определена бинарная операция, которая удовлетворяет аксиомам замкнутости (
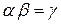), ассоциативности (
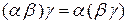), тождественности 
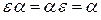), обращения (
).
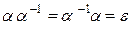В силу того, что бинарная операция, действующая в группе G является коммутативной (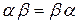
; таблица Кэли является симметричной относительно главной диагонали), группа G является коммутативной или абелевой. Группа G содержит конечное число элементов – восемь, следовательно, группа G является конечной группой восьмого порядка. Каждое из восьми преобразований симметрии может быть получено, например, из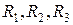 
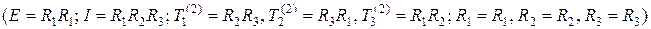– подмножество элементов 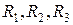называется системой образующих элементов группы G. Это не единственная система образующих – элементы 
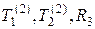также являются системой образующих.
Определение. Группа G, содержащая элементы: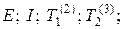 
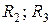, называется группой симметрии объекта G o.
Рассматривая различные механические воздействия на пространственный объект, аналогичным образом в каждом конкретном случае можно определить группы симметрии воздействия Gi.
Дата добавления: 2015-12-17; просмотров: 23; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!