Эффективные определяющие соотношения
Существенным результатом решения задачи в микромеханической постановке является вычисление тензора эффективных модулей упругости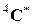 
или тензора эффективных упругих податливостей 
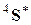, которые определяются как тензоры, связывающие макроскопические тензоры напряжений и деформаций при определенных граничных условиях:
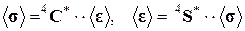(1.3.1)
1.3.1. Кинематические граничные условия Хашина – Розена [15].
Для теоретического построения эффективных определяющих соотношений рассмотрим квазистатическую задачу теории упругости гетерогенной среды (1.1.1), (1.1.2) при кинематических граничных условиях Хашина – Розена:
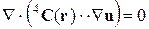(1.3.2)
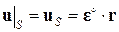, (1.3.3)
где S – поверхность, ограничивающая представительный элемент объема V;
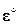– симметричный тензор-константа.
Определив вектор перемещения u, по соотношениям Коши (1.1.5) находим тензор микродеформаций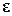 
и вычисляем средний тензор микродеформаций 
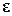. Отметим, что в гомогенной среде при задании граничных условий (1.3.3) тензор микродеформаций равен тензору-константе 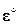. Если рассматривается гетерогенная среда, то тензору-константе 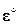равен средний тензор микродеформаций , что легко доказывается, если воспользоваться соотношениями Коши, теоремой Гаусса – Остроградского и специальным видом граничных условий (1.4.3):
(1.3.4)
По найденному тензору микродеформаций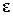 
с помощью определяющих соотношений (1.1.6) определяем тензор микронапряжений 
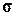и вычисляем 
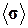. Из решения задачи следует, что каждому тензору 
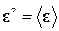соответствует макроскопический тензор напряжений 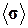. Соотношения, определяющие соответствие между макроскопическими тензорами деформаций и напряжений носят название эффективных определяющих соотношений и имеют вид (1.3.1).
|
|
|
1.3.2. Статические граничные условия Хашина – Розена [15]. Зададим на поверхности S представительного элемента объема поверхностную нагрузку:
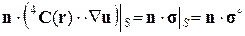, (1.3.5)
где 
– симметричный тензор-константа. Определив вектор перемещения u и тензор микродеформаций 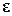, вычисляем средний тензор микродеформаций . В гомогенной среде тензор микронапряжений равен тензору-константе , а в гетерогенной среде тензору-константе равен средний тензор микронапряжений :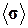
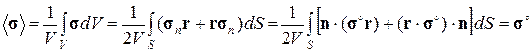, (1.3.6)
где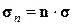 
– вектор напряжения (формула Коши). Из решения задачи следует, что каждому тензору 
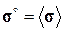соответствует макроскопический тензор деформаций (определяющие соотношения (1.3.1)).
1.3.3. Энергетические соотношения. Обратимся к записи определяющих соотношений в форме (1.1.9) и (1.1.10). Проведем осреднение упругого потенциала, считая, что заданы кинематические граничные условия (1.3.3):
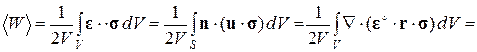
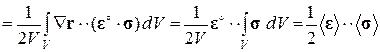(1.3.7)
Сформулируем полученный результат в виде теоремы:
Теорема 1. Если для гетерогенной среды, занимающей объем V и ограниченной поверхностью S, заданы кинематические граничные условия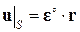 
, соответствующие однородной деформации гомогенной среды, то средний по объему упругий потенциал равен упругому потенциалу для средних деформаций (“эффективному” упругому потенциалу):
|
|
|
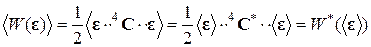, (1.3.8)
а эффективные определяющие соотношения имеют вид:
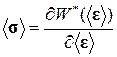(1.3.9)
Осредним упругий потенциал, считая, что заданы статические граничные условия (1.3.5):
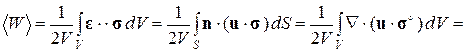
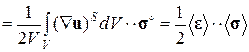(1.3.10)
Сформулируем полученный результат в виде теоремы:
Теорема 2. Если для гетерогенной среды, занимающей объем V и ограниченной поверхностью S, заданы статические граничные условия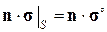 
, соответствующие однородному напряженному состоянию гомогенной среды, то средний по объему упругий потенциал равен упругому потенциалу для средних напряжений (“эффективному” упругому потенциалу):
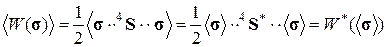, (1.3.11)
а эффективные определяющие соотношения имеют вид:
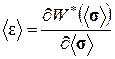(1.3.12)
Эффективные определяющие соотношения в термомеханике композиционных материалов имеют вид:
(1.3.13)
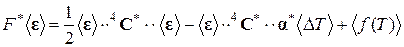, (1.3.14)
где F * – “эффективная” свободная энергия.
Дата добавления: 2015-12-17; просмотров: 20; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!